1引言
近年来,变频调速交流电机在许多工业领域得到了广泛应用。目前,交流调速中使用较多的是鼠笼式感应电机、绕线式感应电机、双馈电机等,但这些电机都有各自的缺点和局限性。容量的不断扩大使得鼠笼式电机的变频容量不断上升,增加了变频器的成本。电刷结构运行不够安全,需要定期维护。无刷双馈电机的产生解决了这些问题。
无刷双馈电机(Brushless Doubly-fed Machine,简称BDFM),定子绕组由两套三相对称绕组组成的,一套为功率绕组,一套为控制绕组。它兼有异步电机和同步电机的共同优点,具有转速和功率因数可调、变频器容量小等特点。无刷双馈电机去掉了转子侧电刷,提高了机械的稳定性,降低了维修成本。
无刷双馈电机是在串极感应电机的基础上发展而来,1893年美国的Steinmetz和德国的Gorges发现将两台绕线转子异步电机同轴串级连接可以获得的一种新的运行方式。采用这种方法可以获得低速运行,并可以在一定范围内调速。随后Hunt提出了Hunt电机。这种电机具有一套转子绕组和一套具有不同极数的定子绕组,并且具有一个共同的磁路。它可以在电阻控制的方式下获得高启动转矩和速度控制,从而实现无刷化。到19世纪70年代,Broadway等对Hunt电机进行了较大改进,简化了转子绕组,使定转子绕组极数配合的范围进一步扩大,极大地推进了无刷异步电机理论的发展。后来Broadway将相调制理论应用到极变换绕组中,从而使定子绕组对称化,简化了定子绕组,使之可以通过对普通双层绕组经过适当的连接来得到,自此,无刷电机开始进入实用化阶段[1]。
目前,无刷双馈电机的研究形成了两大学派:一个重点研究笼型转子结构的无刷双馈电机。其转子是普通的笼形结构,称为无刷双馈感应电机(Brushless Doubly-Fed Induction Machines,简称BDFIM),又称笼型无刷双馈电机。另一个重点研究磁阻转子结构。这种无刷双馈电机称为无刷双馈磁阻电机(Brushless Doubly-Fed Reluctance Machines,简称BDFRM)[2]。这两大学派形成了两套各具特色的分析研究体系。国外对无刷双馈系统的研究已从对电动机结构的改进发展为建立准确实用的数学模型,寻找适合无刷双馈电机的控制策略,促进其进入实用化阶段。国内也从20世纪90年代开始对其进行研究,但是大部分只对这种电机的原理和性能做简单介绍。目前,国内无刷双馈电机这类综述文章很多,但大都不够全面。
2无刷双馈电机原理
无刷双馈电机示意图如图1所示。定子功率绕组极对数为pp,在同步运行时直接接电网;定子控制绕组极对数为pc,同步运行时输入变频电源。转子采用类鼠笼式的自行闭合环路结构,转子极对数为pr=pp+pc。
当功率绕组接入电网(频率为飞fp)、控制绕组接入变频电源后(频率为fe,一般情况下fp≠fp),由于两套定子绕组同时有电流流过,因此在气隙中产生两个不同极对数的磁场,这两个磁场通过转子的调制发生交叉耦合,构成了实现能量传递转换的基础,即“极调制”机理。
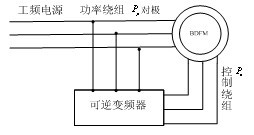
图1 无刷双馈电机示意图
当功率绕组电源正相序联接,控制绕组通过变频器反相序联接时,它们产生的旋转磁场方向相反,同步转速分别见图2,其中np1、nc1分别为功率绕组及控制绕组旋转磁场转速,nr为转子的旋转速度,npr、ncr为两个定子磁场在转子中感应的转子电流产生的旋转磁场转速[3]。

图2电机内部磁场相互作用关系
由电机原理,易知:

则功率绕组在转子绕组感应的电流频率frp为:

当电机定子控制绕组接入频率为 的变频电源,转子绕组感应的电流频率frc为:

由于转子特殊的同心式结构是一个极数转换器,当电机稳定运行时,转子绕组感应的电流频率frp、frc相等,所以,转子机械转速nr为:

由上式可看出,当pp、pc、fp一定时,改变控制绕组频率fc可使电机转速随之改变,当fc=0时的无刷双馈电机的转速称为自然同步速,低于自然同步速的转速称为亚同步调速,反之称为超同步调速[4]。
无刷双馈电机可实现同步、异步运行。同步运行为双馈运行,具有自启动能力,是目前运行较多的方式。
BDFM异步运行时,一套端点连到工频电源上,另一套端点通过滑动变阻器短接,调节电阻的大小就可以在一定的范围内调节电机的速度。
同步运行时,功率绕组接电网,控制绕组由变频电源供电,通过改变功率绕组和控制绕组的供电相序,实现电机的超同步和亚同步调速,同步运行如图1所示。通过改变副绕组供电频率fc以及主副绕组的相序,可使电机的转速高于或者低于同步速。
3 无刷双馈异电机的数学模型
BDFM的数学模型大致分为网络模型、dq数学模型、双同步轴模型3类[5]。
3.1网络模型
由于BDFM的定转子结构与普通电机有所不同,因此其参数计算与传统电机的参数计算有一定区别。定转子绕组的自感、互感可以采用文献[6]中所介绍的网路分析法来加以计算。而定转子绕组的电阻、漏感可以采用传统的计算方法。这样就可获得定子阻抗矩阵Zss、转子阻抗矩阵Zrr以及定转子互感抗矩阵Zrs、Zsr。这些矩阵都是经过一个个线圈分别计算,然后叠加得到的。
经转换,电机方程可表示为: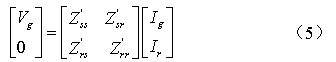
其中:
Z′ss=CTZssC
Z′sr=CTZsr
Z′rs=ZrsC (6)
电磁转矩为:
式(5)、(7)构成了BDFM的网络数学模型,在19世纪末应用较多,后逐渐被dq数学模型取代。
3.2转子旋转dq坐标模型
转子旋转dq数学模型是在网路模型的基础上发展起来的。它进一步简化了网路数学模型,有利于控制方法的实现,目前应用最为广泛。
采用转子旋转dq坐标系时,电机可表示为以下形式:
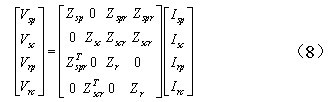
方程(8)经过坐标变换转化为建立在转子速dq坐标下的数学模型[7]:
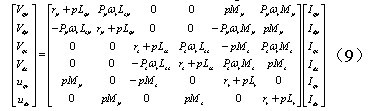
式中:rp、Lsp、Mp分别为功率绕组的电阻、自感和功率绕组与转子间互感,rc、Lsc、Mc分别为控制绕组的电阻、自感和控制绕组与转子间互感,rr、Lr、ωr为转子的电阻、自感和机械角速度,u与i表示电压电流的瞬态值,p为对时间积分,下标p表示功率绕组,下标c表示控制绕组,下标s表示定子侧,下标r表示转子侧。
因为BDFM转子采用自行闭合的环路结构,因此转子d轴q轴电压udr、uqr均为零,从而可进一步简化数学模型。
电磁转矩方程(7)经正交变换得:
Te=Tep+Tec=PpMp(IqpIdr-IqpIqr)+PcMc(IqpIdr+IqpIqr)(10)
式(9)、(10)构成了BDFM的dq数学模型。
3.3双同步坐标数学模型
双同步坐标模型适合于通过控制绕组电流 、 来实现调速的控制策略。当两套绕组具有合适的极对数配合时,BDFM可分解为两个子系统,即功率绕组子系统和控制绕组子系统,两个子系统分别建立以各自定子旋转磁场同步转速的dq坐标时,则各子系统中的电压、电流及磁链的空间向量转换为直流量,解决了交流量不易控制的难题。
将式(9)经变换得:
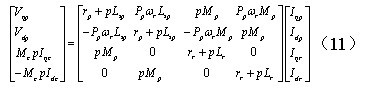
用上标ce表示控制绕组同步坐标系,pe表示功率绕组坐标系,r代表转子坐标系。则:
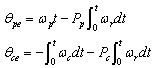
在同步坐标系下,方程(11)变为:
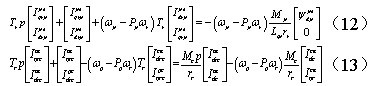
式(12)、(13)分别为功率绕组坐标系和控制绕组同步坐标系下的电机模型。
转矩方程为:
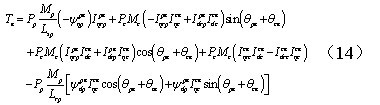
式(12)、(13)、(14)共同组成了BDFM的双同步坐标模型。
4无刷双馈电机的控制策略
几乎所有可用于异步感应电机的控制策略都可以用BDFM的控制中。但是由于BDFM只有一套绕组可控,而一套绕组是不可控的,所以其控制策略与传统异步电机的控制策略有些差异[8]。
4.1标量控制
BDFM标量控制为闭环控制,控制BDFM的电压的幅值和频率的大小,采用稳态等效电路和电压方程,对控制处理器的要求不高,较为简单,但是其动态性能指标较低。图3为文献[9]所述标量控制的框图,通过检测速度测量信号与给定信号产生偏差以调节控制绕组频率实现速度控制,通过检测功率因数测量信号与给定信号产生偏差以调节控制绕组励磁电流或电压实现功率因数控制。
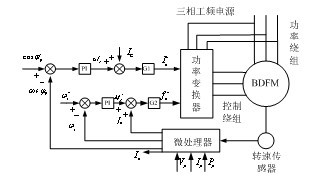
图3 BDFM标量控制框图
4.2矢量控制
矢量控制是通过测量和控制电机电流矢量,根据磁场定向原理分别对电机的励磁电流和转矩电流进行控制,从而达到控制电机转矩和转速的目的。这种控制需要建立BDFM双同步坐标轴系数学模型
4.2.1转子磁场定向控制
通过功率预测系统和电磁转矩估计建立起转子磁场定向的控制算法,以实现BDFM转子磁场定向矢量控制。文献[10]所述转子磁场定向控制框图如图4所示,该控制算法需要测量功率绕组端和转子角速度等数据。其动态性能优良,从控制效果及实现难易考虑,选择此种控制方式对BDFM的传动控制较为合适。
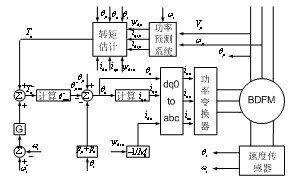
图4 BDFM转子磁场定向矢量控制框图
4.2.2功率绕组磁场定向控制
因为由BDFM矢量模型获得的稳态功率电流d、q轴分量与控制电流d,q轴分量线性相关。而电磁转矩主要由功率电流的绝对值及其d轴分量产生,因此需要确定功率绕组磁场位置,以使用功率绕组磁场定向的参考系。该控制策略简单方便,可以获得较好的动态响应性能,功率绕组电流和有功功率可以调节。文献[11]所述BDFM功率绕组磁场定向控制框图如图5所示。这种控制策略主要应用于风力发电中。
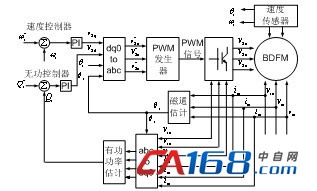
图5 BDFM功率绕组磁场定向矢量控制框图
4.3直接转矩控制
直接转矩控制是借助三相定子电压和电流来计算磁链和转矩,并通过磁链和转矩的直接跟踪实现PWM控制。将电机参数、输入量以及输出量转变成控制绕组电压、电流表示的函数。通过估算磁通和转矩的变化,得到控制绕组的给定电压、电流并与检测量比较以改变控制绕组电压、电流。文献[12]所述直接转矩控制框图如图6所示。直接转矩控制摒弃了矢量控制中的复杂的坐标变换,使控制简单化,性能较为优越。但计算量较大,需要采用高速处理器,成本较高。
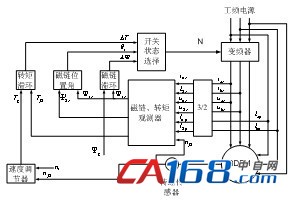
图6 BDFM直接转矩控制框图
4.4智能控制
随着技术的进步,智能控制在各个领域中的应用越来越广泛。主要有模糊控制、神经网络控制、滑模控制、自适应控制等[13]。
在对BDFM此类数学模型较复杂的控制对象进行控制时,使用模糊控制、神经网络控制、滑模控制、自适应控制等智能控制方法,能够加快系统响应,减小超调量和调节时间,提高系统的鲁棒性,实时控制效果好。但是,智能控制策略还有许多理论和技术问题尚待解决,如智能控制器主要依靠经验设计,对系统性能缺少客观的理论预见性。另外,到目前为止,仅仅依靠智能控制还很难理想地解决上面提到的问题,很多情况下它是和其他控制方法结合在一起使用,取长补短,形成交叉综合的控制技术。
5无刷双馈电机应用及发展趋势
BDFM是一种结构简单,坚固可靠的电机。它具有异、同步通用的特点,可以在没有电刷的情况下实现双反馈,从而具有转速稳定、功率因数可调、效率高的优点。因为其功率绕组频率、控制绕组频率和转子旋转频率之间相互依赖。在发电情况下,如果将转差频率的电流或电压加到控制绕组中,就可以实现功率绕组的恒频输出。所以BDFM可应用于转子速度经常变化的系统,如风力发电、水力发电等,十分有效。
如果变频器用于BDFM极数较少的定子绕组,可以大大降低变频器的容量。对于那些中高压的场合,采用BDFM可使开关频率大大提高,系统性能得到优化。而且在变频器出现故障的情况下,BDFM可以作为普通异步电机运行,这对于那些绝对不允许停机的场合十分重要。由此看来,BDFM将在一定程度上取代传统电机,应用于中高压传动领域。
BDFM作为一种新型电机,由于它可以在无刷的情况下实现双馈,速度及功率因数均可调节,既可同步运行又可异步运行,且变流装置只需处理滑差功率,装置容量比电机容量小得多,减小了对电网的污染,因此它必将在不久的将来,在中大容量调速系统和变速恒频发电系统中获得广泛的应用,对节能降耗、提高经济效益有着重大的意义。
作者简介
陈媛(1990-)女 硕士研究生,研究方向为电力电子与电力传动—双馈电机控制。
参考文献
[1]席伟,韩力,高强等.无刷双馈电机的研究现状及发展前景[J].微电机,2010,43(9):80-84.
[2]彭军林.无刷双馈电机及控制研究[D].武汉:华中科技大学,2006.
[3]邓先明,姜建国.无刷双馈电机的工作原理及电磁设计[J].中国电机工程学报,2010,23(11):126-132.
[4]唐海梅.无刷双馈电机的基本原理及实际应用[J].电气传动,2005,35(8):60-62.
[5]张彦锋,潘再平,章玮,贺益康等.无刷双馈电机的研究及应用前景[J].机电工程,1998,(6):55-60.
[6]AlanK. Wallace,R.Spee and Hian K.Lauw.Dynamic Modeling of Brushess Doubly-fed Machine.Conference Record of 1989 IEEE Industry Application Society Annual Meeting,
1989.
[7]Ruqi Li,Alan Wallace and R.Spee.Two-axis Model Development of Cage-rotor Brushleess Doubly-fed Machines.IEEE Trans.Energy Conversion,1991,6(3):445-452.
[8]刘航航,韩力.无刷双馈电机控制策略发展综述[J].特种电机,2010(6) .
[9]Zhou D,Spee R,Wallace A K,Laboratory Control Implementations foe doubly-fed machined[C],19th Annual Conference of IEEE Indusrial Electronics,Control and Instrument-
ation,Maui,Hi,USA,1993:1181-1186.
[10] Zhou D,Spee R,Alexander GC.Experi-mental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[C],IEEE Transaction on Power Electronics Specialists Conference.1996:913-919.
[11]Shao S,Abdi E,McMahon R.Vector control of the Brushless Doubly-fed Machine for wind power generation[C],IEEE International Conference on Sustainable Energy Technologies.2008:322- 327.
[12]刘晓鹏,张爱玲,樊双英等.无刷双馈电机直接转矩控制策略的研究[J].微特电机,2006(3):25-31.
[13]王硕.基于模糊神经网络的无刷双馈电机调速[D].天津:天津大学硕士论文,2006.







共0条 [查看全部] 网友评论