1引言
由于在电压型的双三电平SVPWM矢量控制变频调速系统中整流器和逆变器都采用三电平空间矢量PWM调制,所以不可避免存在直流侧中点电位波动,现以三电平逆变器为例进行直流侧中点电位波动分析,并提出抑制直流侧中点电位波动的控制方法[1]。
2三电平变频器中点电位波动分析
2.1直流侧中点电位不平衡原理[2]-[4]
以三电平逆变器为例,分析中点电位波动的原理。图1为中点电位的分析图。
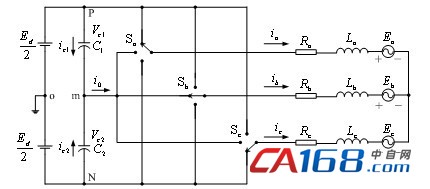
图1 中点电位连接图
对直流母线电容电压有如下关系:

式中:ic1,ic2——电容C1、C2上的电流,参考方向如图1所示;
Vc10,Vc20——电容电压初始值;
假设某时刻工作在稳态,且两电容电压相等,则有:
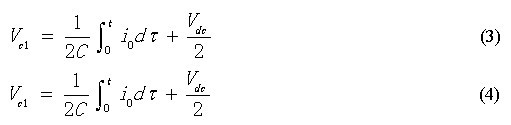
式中,i0——中点电流;
从图1的开关模型可得,中点电位不平衡是由于中点电流对直流环节电容充、放电不均,中点电位波动与中点电流关系可以表示为:
△v=i0/C (5)
由式(5)可以看出,中点电位与i0紧密相关,随i0的大小和方向变化而改变。
2.2各电压矢量对三电平逆变器直流侧中点电位的影响[5]-[8]
已知三电平输出27种电压,各种输出状态所对应的交流负载连接形式不同,对于三电平逆变器的不同输出情况进行分析可以知道,尽管输出状态有27种,对于电容和负载两端的连接状态却只有7种。
2.2.1大矢量对中点的影响
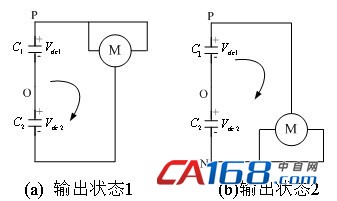
图2 大矢量作用电路结构
如图2所示,图2 (a)的输出状态是(1,1,-1),(-1,1,1),(1,-1,1);图2(b)的输出状态是(1,-1,-1),(-1,1,-1),(-1,-1,1)。两种情况下,三电平逆变器输出为大矢量,此时中点O与负载端无连接,没有电流流通,负载直接与电容C1、C2相连,两电容的充放电时间和充放电电流平均值相同,只要两电容参数一样,中点电位始终保持为Ed/2,所以在大矢量的作用下中点电位不受影响。
2.2.2中矢量对中点的影响
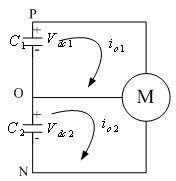
图3 中矢量作用时电路结构
如图3所示,电路输出状态是(1,0,-1) ,(1,-1,0) ,(-1,1,0) ,(-1,0,1) ,(0,-1,1) ,(0,1,-1)。逆变器输出中矢量,负载与两电容的端点均有连接, C1、C2两个电容构成充放电回路,但两个回路的充放电电流存在相位差且随中点电位的波动电流差异累积增大,所以中点电位还是有一定的波动。
2.2.3小矢量对中点的影响
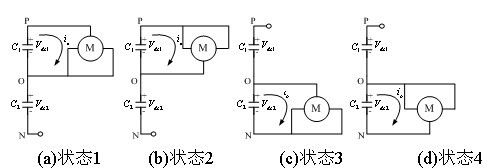
图4 小矢量作用电路结构
如图4所示,图4 (a)的输出状态是(1,0,0),(0,1,0),(0,0,1);图4 (b)的输出状态是(1,1,0),(1,0,1),(0,1,1);图4 (c)的输出状态是(0,-1,-1),(-1,0,-1),(-1,-1,0);图4 (d)的输出状态是(-1,0,0),(0,-1,0),(0,0,-1)。在四种工作状态下,三电平逆变器输出为小矢量。在a,b这种工作状态下,负载仅与电容C1两端相连,给C1构成了一个放电回路,C1在放电电流的作用下端电压下降,而此过程对于C2而言是一个充电的过程,从而C2两端的电压上升,中点电位U0也随着上升;图4 (c)、(d)两种工作状态与图4 (a)、(b)正好相反,给C2构成了一个放电回路,导致C1的端电压上升,C2的端电压下降,中点电位最终下降。
通过以上分析可知,可以看出,小矢量和中矢量对直流侧中点会造成影响,只有大矢量对直流侧中点没有任何影响。
2.3矢量合成时中点电压平衡区域
基于最近三矢量选择方法的中点电压平衡数学模型,在参考矢量位于6个大区的第一区域时,在单采样周期Ts内中点电压可以平衡时调制度m、功率因数角φ和当前参考矢量的方位角θ需要满足: 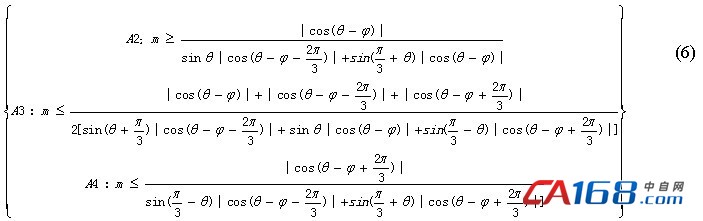
当功率因数角已知时,由式(6)得到θ-m曲线,图5中粗红线表示A2的θ-m曲线,粗绿线表示A3的θ-m曲线,粗蓝线表示A4的θ-m曲线;“曲线1”上方为A2区,“曲线2”上方为A4区,A2区和A4区下方和“曲线3”上方为A3区。
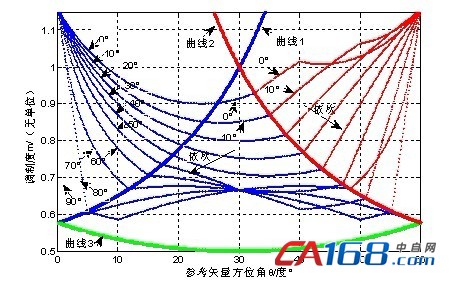
(a) [0,90°]时的曲线
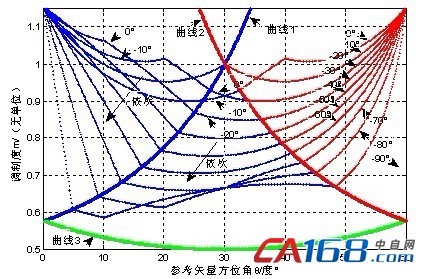
(a) [-90°,0]时的曲线
图5 单采样周期内中点电压平衡关系曲线
从图5可以看出,在单采样周期Ts内当逆变器以一定的频率和调制度m运行时,在一定的条件下中矢量引起的中点电压偏移是可以采用小矢量加以平衡,而调制度m较大的某些区域则是不可能平衡的;并且可以看出,当调制度m一定时,随着负载功率因数的变差,不可平衡的区域逐渐变大。
3三电平有源前端整流器直流侧中点电位控制
通过类比分析可知:对于同一个开关序列,在逆变器中和在整流器中,其对两个电容的中点电位的影响恰好相反。例如,当图6(a)所示的逆变器中的开关序列(1,0,0)时,图6(b)所示的整流器中的开关序列也为(1,0,0),所以其对中点电位的控制方法可以基本沿用新型简化控制方法,只需稍微的改动,在中点电位偏差值的符号反相后,把数值送入整流器的中点电位控制单元中。
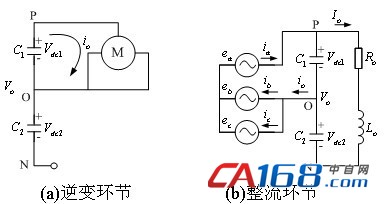
图6 逆变和整流中性点电位变化图
4仿真与实验结果
根据以上方法对三电平变换器中性点仿真后得图7-8所示。
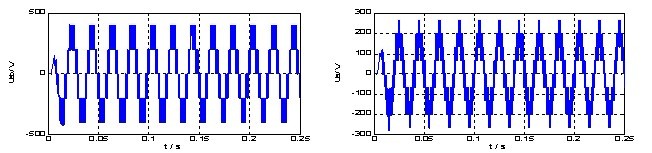
(a)逆变输出线电压 (b)逆变输出相电压

(c)未采取中点控制中性点电压 (d) 采取中点控制后中性点电压
图7 仿真结果
实验以风力发电双三电平变频调速系统为载体,测量仪器采用Agilent 100M模拟数字混合示波器,实验波形如图8所示。
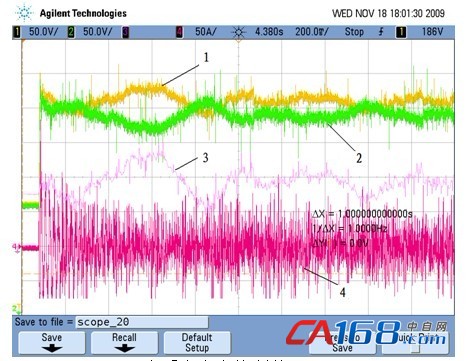
(a) 未采取中点控制前
注:1-上母线电压/ 2-下母线电压/ 3-中点电位/ 4-双闭环无功反馈
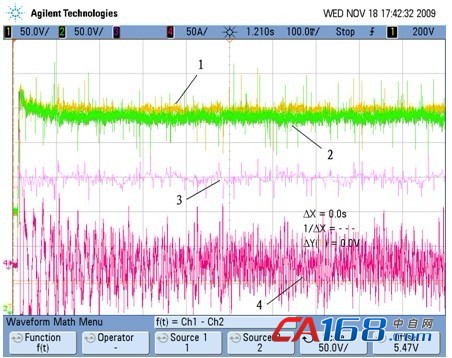
(a) 采取中点控制后
注:1-上母线电压/ 2-下母线电压/ 3-中点电位/ 4-双闭环无功反馈
图8 实验波形
前后实验波形可以看出,图8(b) 采取中点控制后的中点电位比图(a) 未采取中点控制前的中点电位波动更小,更平衡稳定,上下母线电压也更加平稳。
5结束语
由仿真波形和试验波形可以看出,经过对变频器中性点进行软件算法改进后,中性点电压基本平衡,说明对矢量作用的分析是正确的,通过对中小矢量在整流逆变中的作用时间进行软件调整后或得了很好的控制效果。
作者简介
王珂(1985-) 男硕士研究生,研究方向为电力电子与电力传动。
参考文献
[1]李华德.交流调速控制系统[M].北京:电子工业出版社,2003.
[2]宋强,刘文华,严干贵等.基于零序电压注入的三电平NPC逆变器中点电压平衡控制方法[J].中国电机工程学报,2004,24(5):57-62.
[3]郭前岗,李耀华,孟彦京等.现代交流传动系统调速技术综述[J].微计算机信息,2004,20(11):776.
[4]宋文祥,陈国呈,丁肖宇等.基于两类脉宽调制方式本质联系的三电平逆变器中点电压平衡控制的研究[J].电工技术学报,2005,20(12):53-58.
[5]毛鸿,沈琦.PWM整流器的电压控制策略研究[J] .电气传动,2000(3):21-23.
[6]王兆安,黄俊.电力电子技术(第4版)[M].北京:机械工业出版社,2002.
[7]李永东,肖曦,高跃等.大容量多电平变换器-原理、控制、应用[M].北京:科学出版社,2005.
[8]Jae Hyeong Seo, Chang Ho Choi, Dong Seok Hyun.A New Simplified Space-Vector PWM
Method for Three-Level Inverter[J].IEEE Transactions on Power Electronics, 2001,16(4):545-550.







共0条 [查看全部] 网友评论