1引言
温度控制系统广泛存在于化工、石油、造纸、制糖、制药等工业部门,从控制的角度来说,其过程的纯滞后时间与主导时间常数之比往往超过0.5,是大纯滞后过程。在设计控制系统时,需要对过程进行系统辨识,建立对象的数学模型。本文以中药提取罐作为控制对象、以S7-200 PLC作为控制器和辨识器硬件,对中药提取温度控制对象进行系统辨识,建立其数学模型。
2阶跃响应法
在经典的控制系统分析与设计中,通常采用传递函数来描述系统的动态特性。系统辨识就是要建立系统的传递函数。经典的传递函数辨识方法可以分为时域法和频域法两种。传递函数辨识的时域方法又包括阶跃响应法、脉冲响应法和矩形脉冲响应法等,其中以跃响应法最为常用。阶跃响应法利用阶跃响应曲线对系统传递函数进行辨识,阶跃响应曲线即输入量作阶跃变化时,系统输出的变化曲线。利用阶跃响应曲线来确定传递函数的方法很多,常用的有近似法、半对数法、切线法、两点法和面积法等。两点法中最古老也是最有名的方法是Küpfmüller方法,一阶惯性环节加纯滞后环节传递函数的模型参数K、T、τ可以直接从阶跃响应曲线上求得。
3S7-200 PLC
S7-200 PLC是西门子公司开发的小型化的PLC,它的用户程序中可以包括位逻辑、计数器、定时器、复杂数学运算以及与其它智能模块通讯等的指令,对于8个以下闭环的小型控制系统,它也能提供极具价格竞争力的解决方案。STEP 7--Micro/WIN软件中包含了一个PID整定控制面板,它能够以图形的方式来监视PID回路,用于启动自整定序列,取消自整定序列,还可以将推荐整定值或者设计的整定值应用到实际控制中去。本文利用STEP 7--Micro/WIN软件中的PID整定控制面板来输出阶跃信号,采集对象的阶跃响应信号并绘制阶跃响应曲线。
4中药提取罐温度控制数学模型的建立
4.1温度控制对象的传递函数
温度控制系统的实质是控制温度对象的热能吸收和或释放(本系统是通过蒸汽加热溶媒从药材中提取中药,可忽略化学反应及其可能的放热或吸热效应),由热能工程学以及传热学可知,温度对热能传递而言是一个大滞后量。忽略工业生产中的一些次要因素,设计控制系统时,可采用一阶惯性环节加纯滞后环节作为控制模型,其传递函数如下式:

4.2阶跃响应法中的两点法
据式(1)以及传递函数的定义有:

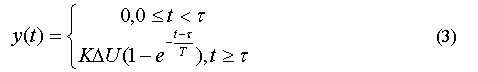

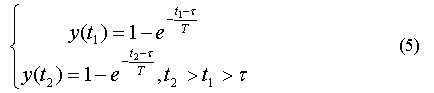
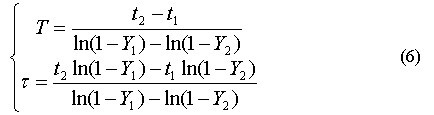


将式(2)后两边取Laplace反变换可得:
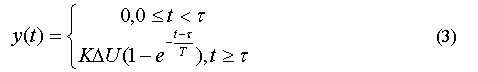
由式(3)进一步可得:

接着,在y(t)上选取两个坐标值(t1,y(t1))和(t2,y(t2)),只要求0, y(t1), y(t2)这三个数值之间有明显的差异即可。化为无因次曲线后得:
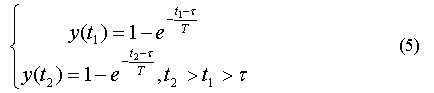
式(5)中的y(t1), y(t2)简记为Y1, Y2。解之得:
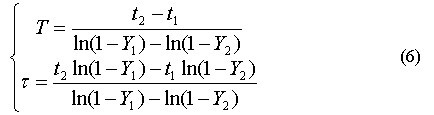
若选择点y(t1)=0.284以及点 y(t2)=0.632,此时有:

根据阶跃响应曲线,综合式(4)及式(7)就可以求出一阶惯性环节加纯滞后环节传递函数式(1)中的模型参数K、T、τ。
4.3阶跃响应曲线的获取
采用STEP 7--Micro/WIN软件编制包含PID控制器的 S7-200 PLC应用程序。连接STEP 7--Micro/WIN电脑与实体S7-200 PLC,启动PLC运行,进入PID整定控制面板。PID整定控制面板图形显示区中用不同的颜色显示了过程变量、设定值和输出值相对于时间的函数。过程变量和设定值共同使用左侧的纵轴,输出值使用右侧的纵轴。PID整定控制面板中的设定值要设定为阶跃信号,过程变量即为阶跃响应信号,输出值为PLC输出到执行器的命令信号。通过设置PID整定控制面板的相关参数,保证设定值及输出值均为阶跃信号以获取真实可靠的阶跃响应曲线。中药提取罐温度控制的阶跃响应曲线如图1所示。
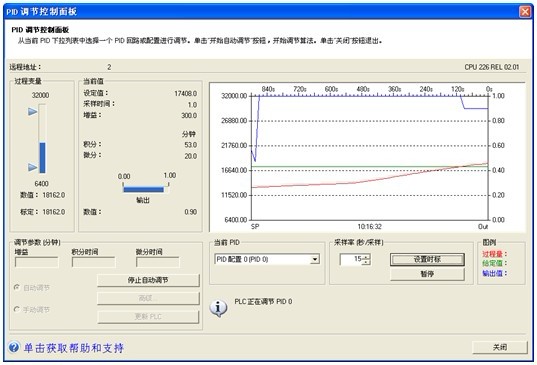
图1 中药提取罐温度阶跃响应曲线图
图中红线是过程量即阶跃响应曲线,绿线是设定值即STEP 7--Micro/WIN软件给PLC的指令,蓝线是输出值即PLC输出给辨识对象的阶跃信号。
4.4模型参数的计算
模型参数计算图如图2所示。
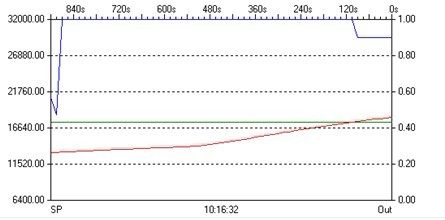
图2 模型参数计算图
模型参数计算图中,有效的辨识时间范围是120s~870s之间,阶跃信号PLC内存储的值为:
ΔU=17408.00-6400.00=11008.00
系统稳态温度值对应PLC内存储的值:
y(∞)= 17408.00 -14368.00=3040.00
于是:
K=0.276163
根据两点法选取点y(t1)=0.284以及点 y(t2)=0.632,换算为PLC内存储的值分别是:15231.16和16289.28;从图上读出相应的横坐标时间值大约是:434和298;据此计算:
t1=870-464=406s
t2=870-328=542s
最终得到:
T=204s,τ=338s
于是对象的传递函数为:

5结束语
系统辨识采用的是阶跃响应法中的两点法。从本质上说,两点法是一种图形的方法,在绘图读数时会带来误差,影响模型的精度;项目采用S7-200 PLC绘图,图形精度可以保证。但仍存在读图误差。
项目的PID控制器基于识别出来的对象模型进行设计,通过现场的调试,达到了由环境温度(调试投运时是21℃)上升到目标温度85℃历时17分钟,仅仅有0.8℃超调,温度误差±1℃的技术指标。
作者简介
杨津听(1969-)男 1992年7月毕业于哈尔滨科学技术大学,获学士学位,主要研究方向为电力拖动自动控制系统,DCS系统,MES系统,先进控制系统,非线性系统、混沌系统。2009年4月毕业昆明理工大学,获工程硕士学位;就职于昆明电器科学研究所,技术部部长,高级工程师;当前研究课题:1、炼锌矿热电弧电阻炉尾气综合利用关键技术研发(云南省科技厅立项编号2010CF017),2、轧钢生产过程棒材穿水冷却智能控制系统研发(云南省科技厅立项编号2010CF003)。
参考文献
[1]李鹏波,胡德文,张纪阳,谢红卫等.系统辨识[M].北京:中国水利水电出版社,2010(12).
[2]王树青.先进控制技术及应用[M].北京:化学工业出版社,2001(7).
[3]方崇智,萧德云.过程辨识[M].北京:清华大学出版社,1988(8).





共0条 [查看全部] 网友评论