1前馈网络
人工神经网络是人类对其大脑神经网络认识理解的基础上人工构造的能够实现某种功能的神经网络。它是理论化的人脑神经网络的数学模型,是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统。在神经网络的网络连接结构中,前馈网络是比较基础的一种结果形式,因而其应用也比较广泛。
前馈神经网络的结构形式分为多层和单层,应用较多的多层前馈网络相邻层间连接,不能隔层连接,没有反馈。图1是一个两层前馈网的拓扑结构。
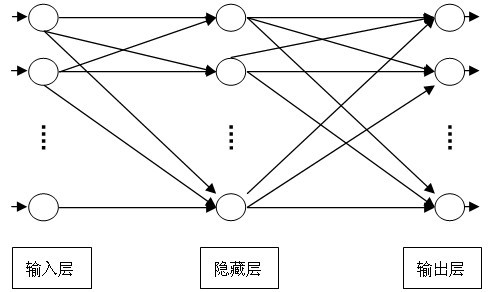
图1 双层前馈神经网络结构
前馈网络的应用有多种,其网络的应用中比较多的有BP网络和径向机网络,其中应用比较广泛的是BP算法,因此本文主要讨论BP算法下的前馈神经网络。
2BP算法及其改进
BP算法主要用来对BP网络进行训练,BP网络执行的是有导师训练,训练过程是根据样本集对神经网络的联接权进行调整的过程。BP算法有着很强的数学基础,因此在训练过程中它对联接权的修改是很让人信服的。
BP算法主要包括4步,这4步可分为两个阶段[1]:
(1)向前传播阶段:此阶段样本输入由输入层经隐藏层传播到输出层,每一层神经元的状态只对下一层神经元的状态产生影响,且此传播过程中各层的权值不变,最终是计算出网络的实际输出。
(2)向后传播阶段:此阶段的主要任务是按极小化误差的方式调整权矩阵。在开始调整神经元的联接权时,只可以求出输出层的误差,再反向逐层后推得到其他层的误差,在向后传播过程中对每个层的各个神经元的权值进行修改,使误差信号趋于最小。
由上所述的BP算法的过程,就可知网络训练过程的具体可按如下描述进行。
输入样本集:
S={(X1,Y1), (X2,Y2),…(Xs,Ys)}
网络根据(X1,Y1)计算出实际输出O1和误差测度E1,对W(1),W(2),…W(M)各做一次调整;在此基础上,再根据(X2,Y2)计算出实际输出O2和误差测度E2,对W(1),W(2),…W(M)分别做第二次调整……如此下去。直至这次循环最后再根据(Xs,Ys)计算出实际输出Os和误差测度Es,对W(1),W(2),…W(M)分别做第S次调整。
上过程是对样本集中的样本的一次循环,而后要将这个循环重复下去,直到整个样本集的误差测度的总和满足系统的要求为止。
基本的BP算法有它自身的缺点,实际应用中所选择的训练算法大都是改进的BP算法。
BP算法的改进主要有采用启发式学习算法改进和基于数值最优化理论改进的两种途径[2]。
第一种:启发式学习算法,是对于网络的表现函数梯度加以分析,从而改进算法,这类的算法主要包括有动量的梯度下降法、有自适应lr的梯度下降法、有动量和自适应lr的梯度下降法和能复位的BP训练算法。
加入了动量后的梯度下降法,降低了网络对于误差曲面局部细节的敏感性。梯度下降法在修正权值时,只是按照k时刻的负梯度方向修正,并没有考虑到以前的积累的经验,即以前时刻的梯度方向,从而常常使学习过程发生振荡,收敛缓慢。为此在算法中加入了动量因子,可以由这个动量因子和前次循环的负梯度产生联系,这样就减小了学习过程的振荡趋势,从而改善了收敛性,提高了学习速度并增加了算法的可靠性。
自适应lr梯度下降法,主要是改善训练过程中的学习速率的,学习速率对于整个训练过程有很大的影响,训练成功与否与学习率的选取关系很大。如果在训练过程中合理地改变学习率,会避免以上的缺陷。有自适应lr的学习算法就能够自适应调整学习率,从而增加稳定性,提高速度和精度。
第二种:优化算法是基于数值最优化理论的算法,主要有共轭梯度法、高斯—牛顿法和Levenberg-Marquardt方法。
共轭梯度法是梯度法的一种改进方法,其基本思想是寻找与负梯度方向和上一次搜索方向共轭的方向作为新的搜索方向,从而加快训练速度,并提高训练精度,它可以改善梯度法振荡和收敛性差的缺陷。而确定新一轮搜索方向的公式中的修正系数的选取方法有不止一种,因此就此衍生出几种不同的共轭梯度法。拟牛顿算法也是一种较好的训练算法,它是对牛顿算法的一种修改。牛顿法的收敛速度比共轭梯度法更快,特别是对于维数较高的问题有明显的优越性,但在牛顿法的每一次迭代中,都需要求出表现函数的二阶导数——Hessian阵,计算量就会很大。拟牛顿算法就是寻找一组算法来代替Hessian阵,又能很好的逼近,这样就保持了收敛速度快的优点,又减小了计算量。Levenberg-Marquardt方法适用的情况是表现函数是平方和的形式,那么就不再需要计算Hessian阵,可以用这样的矩阵:H=JTJ来近似替换,其梯度为:g=JTe。其中,是雅克比矩阵,它含有网络训练误差的一阶导数,是权值和阈值的函数。E是网络训练误差矢量。则xk+1=xk[JTJ+uI]-1 JTe
当u=0时,就变成具有近似Hessian阵的牛顿法。当u=1较大时,LM算法就更接近小步长的梯度法。在迭代过程中,如果训练成功,就减小u的值;如果训练失败,就增加u的值,这样表现函数最终会减小到一定值。
3实际应用中的改进
在近几年的关于神经网络的应用中,前馈网络的应用还是比较多的。主要应用在预测[3] [4],非线性时间序列模型预测[5][6],分类[7],识别[8]等方面。但在实际应用中,对前馈网络的改进还是始终存在的。改进方法主要有以下几种。
(1)改变隐藏层神经元的输入函数。将输入函数由线性函数改为线性函数的倒数——分式线性函数,由此形成了一种新的神经网络结构,分式线性神经网络[9]。此种神经网络可无限逼近Rm 上无界闭子集到Rn 上的在无穷远有极限的任意连续映射, 并且有相应的证明,因此扩充了BP 神经网络的非线性逼近能力。并且给出了实现分式线性神经网络逼近有界或无界区域上连续映射的反向传播算法。
(2)和其他算法相结合
(a)粒子群优化算法与BP 神经网络相结合[10], 用粒子群优化算法优化神经网络参数, 改善神经网络预测模型的收敛性能[11]。粒子群中每个粒子的维度分量都对应于神经网络中一个连接权值或阈值. 即神经网络中有多少个连接权值和阈值, PSO中的每个粒子就有多少维。
结合粒子群算法可以利用粒子群的强大的全局搜索能力,可以较好解决BP网络的局部极小值的问题,但是这时因搜索范围的增大往往忽略了搜索的精度,因此又有一种兼顾搜索精度的方法,就是将拟牛顿算法和PSO结合起来进行对网络进行训练的方法[12],这种方法同时兼顾了搜索中的全局最优和搜索精度。
(b)遗传算法和正交变换的前馈网[13]。用遗传调整输入和隐藏层的连接权值和参数,同时用正交变换来确定隐藏层和输出层的连接权值和参数。以使整体达到最优。此外,也有单独应用遗传算法与神经网络相结合[14]的应用方法,以提高网络的性能。
(c)演化计算[15]。将人工神经网络和演化计算相结合,克服神经网络存在的一些不足,构造了一个演化神经网络预测模型作为一种全局优化搜索算法,演化计算能够在复杂的、多峰值的、不可微的大矢量空间中迅速有效地寻找到全局最优解,从而有效地改善神经网络易陷人局部最优的不足,而且对于神经网络的演化学习算法来说,只要能建立起正确的适应度函数,就可对各种结构的网络实施有效地学习,从而打破网络结构和神经元类型对学习算法的限制。
先用演化计算对网络的规模和权值同时进行全局优化,确定最终解的可能区域,然后用BP算法进行局部优化, 从而加快学习过程的收敛速度。
(3)改变传统BP算法的误差函数,用一种最优停止法对网络进行训练,并在训练过程中引入验证样本集, 对训练过程进行整体的监控, 有效地避免了过拟合现像[16]。
神经网络的泛化能力是指学习后的神经网络对测试样本作出正确反应的能力对神经网络学习过程中的训练和测试误差进行研究,发现随着训练误差的减少泛化误差最初也逐渐减小,达到最小点后,尽管训练误差继续减小,泛化误差反而逐步增加,出现了所谓的过拟合现象。而提出的最优停止法能有效地避免过拟合现象。最优停止法的应用关键就是确定学习算法在何时停止,即得到泛化误差最小点.应用最优停止法时,在训练之前将收集到的样本数据集随机地划分为训练集、验证集和测试集,其中测试集可选。训练集用于对神经网络进行训练,验证集用于监控网络训练进程。训练网络时,将网络训练与网络验证交替进行。当网络开始进入过拟合时,验证误差就会逐渐增大,网络训练应提前停止,同时
返回验证误差取最小值时的网络参数。
将误差函数进行改进,因此反传算法也应做相应的改动, 其改动如下所述:对于样本p,设其网络输出为y^p,期望输出为yp,则对应于该样本的误差函数为: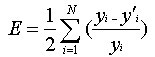
BP网络连接权和阈值的学习算法就变为:
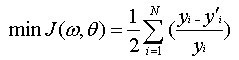
原有的BP网络训练中,并未考虑每个样本中被预估变量(即变量y)的数值大小,在网络终止训练时,其优化的结果往往是每个样本拟合的绝对误差较小。然而在实际应用中,有些过程的被预估变量变化范围很大,利用原有的BP算法的误差函数训练,其优化的最终结果可能是:每个样本拟合的绝对误差较小,但相对于被预估变量值较小的样本而言,其相对误差可能会较大。这样,便会出现拟合不均的现象,即被预估变量值较大的样本拟合程度要好于被预估变量值较小的样本。对误差函数进行改进,这样,在网络终止训练时,其优化的结果是每个样本拟合的相对误差较小,从而使每个样本都得到较好的拟合。
(4)在神经网络中加入先验知识[17]。设计神经网络时隐藏层的激活函数选用基于先验知识的函数,或者在调整权值时也使用一些可以体现先验知识的函数进行调整。
4在人脸检测上的一个应用
神经网络在模式识别领域的应用也是很广泛的,最后在这里给出前馈神经网络在人脸检测上的一个应用。

图2 神经网络的训练图
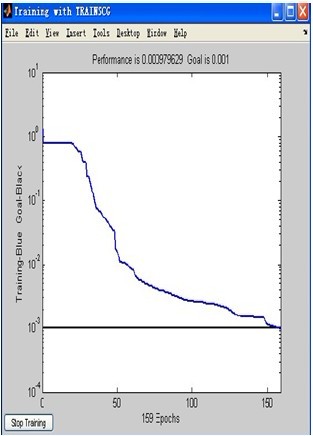
图3 训练过程图
依据人脸检测和神经网络的原理,设计步骤如下:
(1)选择一定量的适合的人脸图片和非人脸图片,进行几何尺寸处理,使训练图片统一。(2)搭建前馈神经网络,为网络选择合适的网络结构和训练函数。
(3)依次输入训练图片,包括人脸图片和非人脸图片,训练网络的参数至网络分类成熟。(4)给网络任意包含人脸的图片作为检测,神经网络会分块遍历整幅图片,分块进行是人脸块和非人脸块的分类。若当下图像块被分为人脸类,则在此人脸处标记。
完成神经网络的训练,其训练过程图如图2、图3所示,图2为网络训练过程中一些参数的实时情况,图3为训练结果随迭代次数达到训练目标的过程。
用训练好的程序进行人脸检测效果图如图4、图5所示。可见神经网络对于人脸的分类结果还是有较高的检测率的,图4为有漏检的情况。

图4 人脸检测效果图

图5 有漏检的情况
作者简介
李爽(1988-) 女 在校研究生,就读于山东大学,研究方向为模式识别与人工智能,图像处理。
参考文献
[1]蒋宗礼.人工神经网络导论[M].北京:高等教育出版社,2001:39-48.
[2]董长虹.Matlab神经网络与应用[M].北京:国防工业出版社,2005:106-109.
[3]厉英,王正,敖志广,翟莹莹,庞维成等.BP神经网络漏钢预测系统优化[J].控制与决策,2010,25(3):453-456.
[4]陈果.神经网络模型的预测精度影响因素分析及其优化[J].模式识别与人工智能,2005,18(5):528-534.
[5]Wei Wu,Dong Nan,Zhengxue Li,Junfang Wang. Approximation Capability to Compact Sets of Function and Operators by Feedforwd Neural Network.82-87.
[6]李俊花,孙昭晨,崔丽,贾旭等.基于新息理论的变点检测及其在长输管道泄漏监测中的应用[J].自动化学报,2006,32(3):462-469.
[7]姚宏亮,张佑生,王浩,汪荣贵等.基于PS_EM算法和BP神经网络的影响图模型选择[J].模式识别与人工智能,2007,20(2):185-190.
[8]康春玉,章新华.基于多人决策理论的船舶辐射噪声识别[J].控制与决策,2007,22(9):1077-1080.
[9]杨国为,王守觉,闫庆旭等.分式线性神经网络及其非线性逼近能力研究[J].计算机学报,2007,30(2):189-199.
[10]Richard L. Welch, Stephen M. Ruffing, and Ganesh K. Venayagamoorthy, Comparison of Feedforward and Feedback Neural Network Architectures for Short Term Wind Speed Prediction. Proceedings of International Joint Conference on Neural Networks,2009:3335-3340.
[11]王安娜,陶子玉,姜茂发,田慧欣,张丽娜.基于PSO和BP网络的LF炉钢水温度智能预测[J].控制与决策,2006,21(7):814-820.
[12]Hiroshi Ninomiya, Particle with Ability of Local search Swarm Optimization: PALSO for Training of Feedforward Neuarl Networks. 2008 International Joint Conference on Neural Networks,2008:3009-3014.
[13]Jinhua Xu Yue Lu,Daniel W.C.Ho.A Combined Genetic Algorithm and Orthogonal Transformation for Designing Feedforward Neural Networks. Third International Conference on Natural Computation 2007.
[14]Iulian-Constantin VIZITIU,Florin POPESCU. GANN System to Optimize both Topology and Neural Weights of a Feedforward Neural Networks.2010:221-224.
[15]朱明峰,熊焰,洪天求等.一种基于演化神经网络的资源型城市可持续发展指标预测模型[J].模式识别与人工智能,2005,18(4):496-501.
[16]杨强大,王福利,常玉清等.基于改进BP神经网络的菌体浓度软测量[J].控制与决策,2008,23(8):869-878.
[17]Fei Han1,Qing-Hua Ling. A New Learning Algorithm for Function Approximation By Incorporating A Priori Information Into Feedforward Neural Networks .Third International Conference on Natural Computation ,2007.







共0条 [查看全部] 网友评论