1引言
无模型控制是指受控系统控制器的设计不包含受控系统任何数学模型信息的控制理论与方法。无模型自适应控制（MFAC）在1993-1994被提出，其基本思想是利用一个新引入的伪梯度向量的概念，用动态线性时变模型，例如偏格式线性化模型来替代一般非线性系统，并仅用受控系统的I/O数据来在线估计系统的伪梯度向量，从而实现非线性系统的无模型自适应控制。作为一种调制方式，很多专家、学者将该控制方法用于直线电机控制邻域中，但是很少有人用于异步电机控制中[1-2]。由于无模型自适应控制无需受控系统的数学模型，所以解决了两个现代控制理论最重要的问题，即未建模动态和对受控系统模型、参数的依赖问题。本文将此控制方法应用于异步电动机的转差频率矢量控制中，使其具有控制精度高，反应速度快等优点，同时减少系统稳态误差。
本文首先单独搭建参考文献[8]中异步电动机的转差频率矢量控制系统，其控制电路主要包括电流调节器和速度调节器。通过对异步电动机的转差频率矢量控制系统的仿真分析发现，系统存在比较明显的缺陷。为此，本文将无模型自适应控制器应用其中，使该控制器与异步电动机转差频率矢量控制系统构成前馈补偿，其在传统PI的基础上增加一个改进的MFAC（无模型自适应控制器）的外回路，来解决由于参数不确定性和结构不确定性引起的控制品质。如果控制效果已经达到理想的状态，则受控对象的输出就己经跟踪了期望信号，MFAC的输出控制信号也就不变化，此时相当于MFAC外环已经断开从而使系统动、静态特性得到了很大的改善。
2无模型自适应控制器的设计
给定期望轨迹yd（t），控制目标是寻找一个合适的控制输入序列u（t），使得跟踪误差e(t)=yd(t)-y(t)，随着时间t趋于无穷而收敛于零。
考虑如下控制输入指标函数：
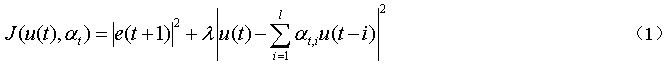
其中αt=（αt，1，αt，2，…αt，I）T，
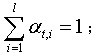u（t-1），u（t-2），…，u（t-l）为前l次采样时刻的控制输入，在第t时刻均已知；λ是一正的权重因子，作用是限制控制输入量变化，克服稳态跟踪误差[3-5]。在MATLAB软件环境下建立无模型自适应控制器仿真模型如图1所示。
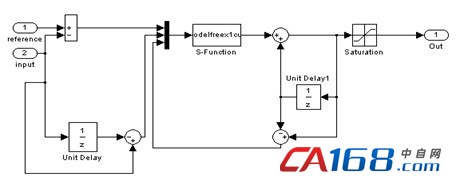
图1无模型自适应控制器仿真模型
3无模型自适应控制器应用于异步电动机转差频率矢量控制系统
异步电动机矢量控制是通过坐标变换将异步电动机数学模型等效为直流电动机，实现了电机转矩和磁通的解耦，到达对瞬时转矩的控制[6-7]。磁场定向控制有两种实现方法：磁通直接反馈型和磁通前馈型（也称作转差频率矢量控制）。目前，实用中较多采用后者，由于其没有实现直接磁通的闭环控制，无需检测出磁通，因而容易实现。
图2所示为在MATLAB软件环境下建立前馈补偿异步电动机转差频率矢量控制系统仿真模型，仿真参数完全按照参考文献[8]中144页所做，其中在0.3s时，外加负载转矩。图3为图2Calculation模块的展开图，系统速度调节器（ASR）的输出信号是转矩给定Te*。在i*qsCalculation模块中，根据转矩给定Te*和转子磁通Phir来计算得出定子电流的转矩分量*qs，显然是给定值。DQ-ABC模块完成d、q坐标系到三相定子坐标系的变换，在这个模块中，根据定子电流在d、q坐标系中的分量，经过旋转变换，得到电动机定子的三相绕组电流的给定值I*abc。在ACR（电流调节器）模块中采用滞环控制原理来实现电流的调节，使得实际电流跟随定子电流的变化。Teta Calculation模块的作用是计算θ角，也就是d轴的位置。DQ-ABC环节的作用是根据θ角，将实际的电动机定子电流Iabc变换得到d、q坐标系中的分量Id和Iq。I*dsCalculation 模块的作用是根据定子电流的励磁分量Ids计算转子磁通Phir[8-10]。
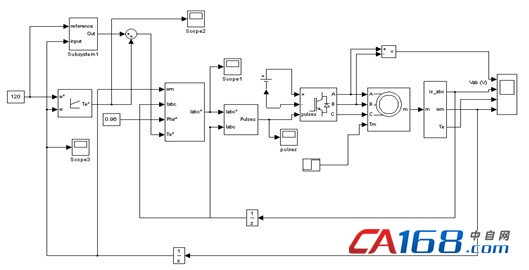
图2 补偿后异步电动机转差频率矢量控制系统仿真模型
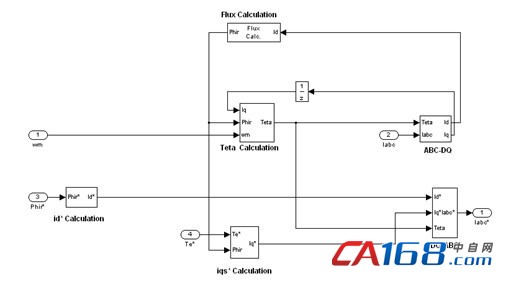
图3 Calculation模块展开图
4仿真结果分析
取与参考文献[8]中144页相同的仿真参数，得到如图4-图9的仿真结果。
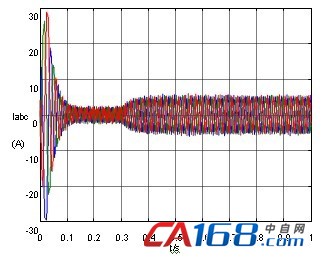
图4 补偿前异步电动机定子电流输出
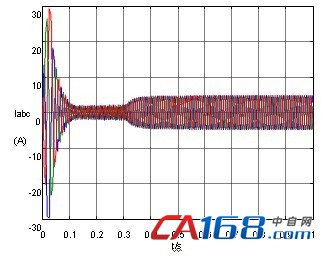
图5 补偿后异步电动机定子电流输出
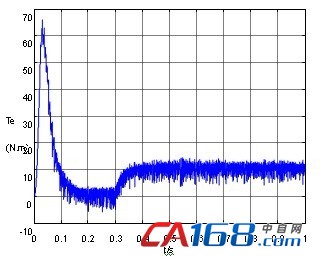
图6 补偿前异步电动机电磁转矩输出
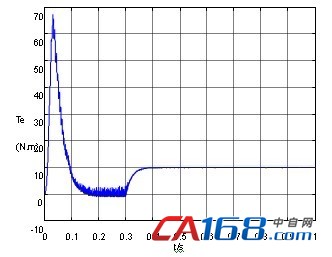
图7 补偿后异步电动机电磁转矩输出
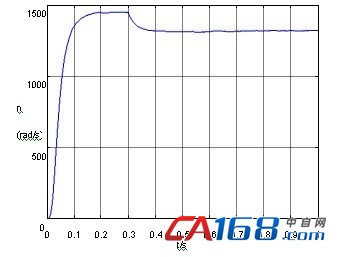
图8 补偿前异步电动机转速输出
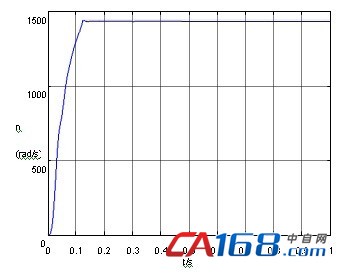
图9 补偿后异步电动机转速输出
比较图4和图5，图6和图7，图8和图9可以发现经补偿后的系统输出的稳态性能要明显优于原系统，具体表现在以下几个方面：文献[8]系统达到稳态以后定子电流纹波和毛刺比较大；输出转矩振荡严重；转速输出值接近1460，但其稳态特性差，有少量纹波。经补偿后的系统定子电流纹波和毛刺、输出转矩振荡、转速纹波基本得到消除。
5结束语
将无模型自适应控制器引入异步电动机转差频率矢量控制系统，克服了对受控系统模型、参数的依赖的缺点，使该系统的稳态特性得到了很大的改善。改进后的仿真试验表明，此控制方法可靠、稳定，控制电路简单、实用，可推广应用于其它电路中。
作者简介
郭建华（1983-）男 硕士，电气工程师，毕业于东北大学，现就职于三一重型装备有限公司，已发表论文多篇。
参考文献
[1]王伟进.直线电机的发展与应用概述[J].微电机，2003，37（1）：45-46.
[2]侯忠生.非线性系统参数辨识、自适应控制及无模型学习自适应控制[D].沈阳：东北大学
博士论文，2003.
[3]曹荣敏，侯忠生.无模型控制方法在直线电机控制中的仿真研究[J].系统仿真学报，2006，
18（10）：2847-2875.
[4]Brian Cronin，Mark W. Spong，Switching Control of Multi-Input Cascade Nonlinear
Systems[C]/ /In Proceedings of the IEEE Conference on Decision and Control，Maui，
2003，4277-4282. Hawaii USA.
[5]Wei Lin，Tielong Shen. Robust Passivity and Feedback Design for Minimum-phase Nonlinear
Systems with Structural Uncertainty [J].Automatica(S0005-1098)，1999，35-47.
[6]陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，2003.
[7]周渊深.交直流调速系统与MATLAB仿真[M].北京：中国电力出版社，2007.
[8]王忠礼，段慧大，高玉峰.MATLAB应用技术[M].北京：清华大学出版社，2007.
[9]王丽敏，王德明.无速度传感器转差频率控制系统的研究[J].电工技术学报，2000，15（2）：
70-72.
[10]朱耀忠.电机与电力拖动[M].北京：北京航空航天大学出版社，2005.
共0条 [查看全部] 网友评论