1引言
同步电机功率因数高、过载能力大、体积小及省维护,使得其在生产实践中得到了广泛的应用。传统的矢量控制使同步电机的动静态性能大大提高,但为分析方便,大都没有考虑转子阻尼绕组的影响,而且存在磁场定向不准的问题[1]。针对这些问题,本文研究了基于无源性的同步电机控制系统。
无源性控制是Romeo Ortega等人从机器人控制的研究中发展起来的。机电系统的无源性控制主要是从能量方程入手,通过状态反馈或输出反馈使得电机的闭环系统表现为一个无源性系统,并根据电气和机械控制目标设计控制器,由无源性和稳定性的关系可以保证整个电机系统的稳定性[2,3],从而达到控制电机的目的。
目前无源性控制主要应用于异步电机中,同步电机的无源性控制研究还不多[4,5]。陈峰等研究了隐极式同步电机的无源性控制器设计,但是没有考虑对任意给定的时变转速的跟踪控制[1];薛花等研究了同步电机基于转子磁链定向的无源性控制研究[2];马良河等研究了同步电机基于定子磁链定向的无源性控制研究[3]。本文从无源性控制方法出发,研究基于气隙磁链定向的间接矢量控制,从而保证对期望转速的有效跟踪,对磁场的方向和幅值的控制。
2同步电机E-L数学模型
同步电机在两相同步旋转dq坐标系下的电压方程和电磁转矩平衡方程如下所示[6]: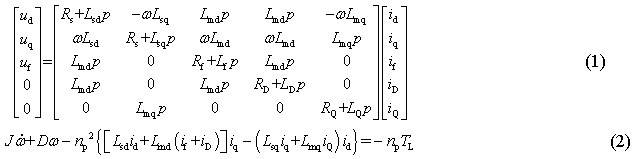
其中:ud、uq、uf分别为定子d、q轴电压和励磁绕组电压;id、iq、if、iD、iQ分别为定子绕组d、q轴、励磁绕组和阻尼绕组d、q轴电流;Rs、Rf、RD、RQ分别为定子、励磁绕组电阻和阻尼绕组d、q轴电阻;Lsd、Lsq、Lf、LD、LQ分别为定子绕组d、q轴、励磁绕组和阻尼绕组d、q轴自感;Lmd、Lmq分别d、q轴电枢反应电感; J为转动惯量;D为机械阻尼系数;TL为负载转矩;np为极对数;p为微分算子;ω为转子旋转角速度;将电气方程和转矩平衡方程结合在一起,并进一步进行整理,可得到同步电机E-L形式的电气—机械系统方程,如下所示:

u1,u2,u3为控制变量:

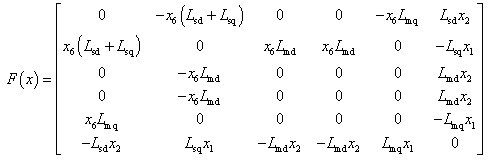
F(x)为反对称矩阵,即xTFx=0,G为对角正定矩阵。取正定二次型能量函数:

对其求导后,代入式(3)整理可得:
两边同时积分,可得:
式(6)左边为整个电动机系统能量的增量,右边为外部电源供给电动机的能量,系统能量增量的总和小于外部注入能量的总和,则电动机系统是严格无源的。
3控制器设计
3.1磁链、转矩控制器设计
在电机控制系统中,有两个控制目标:一个是机械控制目标;一个是电气控制目标[5]。以期望转矩的渐近跟踪为主要目标,设计转速控制环,以实现了对转速的有效跟踪。在研究机械目标是实现的同时,考虑电机磁场的方向和幅值的跟踪控制,即同时实现了电机磁场的矢量控制。本文借鉴矢量控制系统中的气隙磁场定向方法来设计控制器,实现间接跟踪磁场的方向和幅值。
对于同步电机气隙磁链,因为它穿过气隙与定子和转子绕组相交链,它不包含定子漏磁链,所以气隙磁链在d、q轴上的分量分别为:
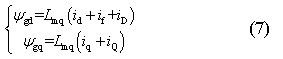
则控制系统希望实现下列控制目标:
(1)电磁转矩渐近跟踪期望转矩
Te-Td→0 (8)
(2)气隙磁链d轴分量渐近趋向于常数
Lmq(id+if+iD)→M (9)
(3)气隙磁链q轴分量渐近趋向于零:
Lmq(iq+iQ)→0 (10)
其中,式(8)现了机械控制目标,式(9)、(10)了电气控制目标,即间接的矢量控制。设期望状态变量为:xd=[x1d x2d x3d x4d x5d x6d]T,若要满足上述控制目标,则需满足下列约束方程:
Np[(Lsd-Lsq)x1dx2d+Lmdx3dx2d+Lmdx2dx4d-Lmqx1dx5d]=Td
Lmq(x2d+x5d)=0
Lmd(x1d+x3d+x4d)=M
假设定子电流、转子励磁电流和转子转速都可以准确测量,可得期望轨迹设计器如下
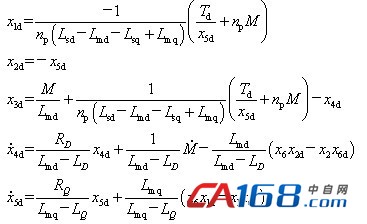
设计控制变量为:
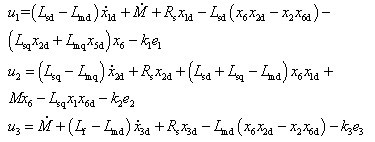
其中e=x-xd为跟踪信号误差,将e代入式(3)可得误差系统的动态方程为:
取误差系统的正定能量函数为:
求导后代入式(12)中,可得:
由Lyapunov稳定性定理第二法[8]可得,若式(13)小于0,则e渐近收敛到0。因此,可令h=-Ke,K=diag(k1 k2 k3 k4 k5 k6)其中,k1,k2…k6均大于0,K为阻尼系数,大小决定了e→0的速度。则有
此时,只要反馈系数K选取合适,所设计的控制器就一定能实现对转矩渐近跟踪和对气隙磁场矢量的渐近控制。系统在获得期望跟踪性能的同时,也保证了稳定性。
3.2转速控制器的设计
为了实现对给定转速的跟踪,转速外环建立转速误差反馈,采用PI控制器,就可以得到参考转矩
Td=-kp(x6-x6d)-kiſ(x6-x6d)dt (15)
其中,kp、ki分别为比例增益和积分增益。
4仿真验证
用于仿真的同步电机参数[9]为:Rs=0.142Ω;Rf=0.375Ω;RD=RQ=0.823Ω;np=4;J=0.058kg·m2;D=0.01N·(m/s);M=3;Lsd=0.852H;Lsq=0.952H;Lmd=0.423H;Lmq=0.423H;Lf=0.823H;LD=0.823;LQ=0.623H。
采用MATLAB/Simulink对同步电机无源性控制系统进行仿真验证。系统以1N·m的负载转矩启动,在0.5s时给定转速为200r/min的斜坡信号,3s时突加负载为8N·m,定转子磁通为3Wb,可得电机的转速、电磁转矩、三相定子电流以及定子d、q轴电流和励磁电流的跟踪波形如图1所示。
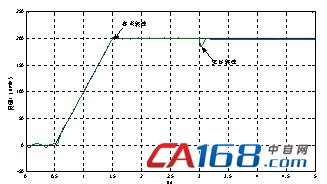
(a) 期望和实际转速波形
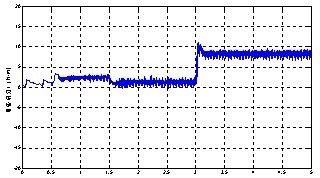
(b) 电磁转矩波形

(c) 三相定子电流ia、ib、ic波形

(d) 期望和实际定子电流id波形
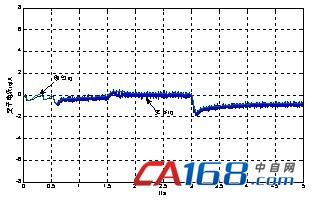
(e) 期望和实际定子电流iq波形
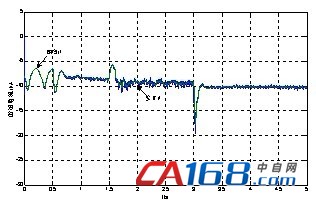
(f) 期望和实际定子电流if波形
图1 仿真波形
仿真结果表明电机实际转速能够很好地跟踪给定转速,当负载发生变化时,转速在很短的时间内能恢复稳定;电机电磁转矩可以较快地跟踪负载转矩的波动;图1(c)为三相定子电流,输出波形明显呈现出正弦波;(d)、(e)、(f)分别为定子d、q轴电流和励磁电流的跟踪波形,由波形可以看出电流能够很好地跟踪期望电流,从而实现对电流的有效控制。
5实验结果
实验系统主要由DSP 28335控制板、逆变器、驱动电路及同步电机等部分组成。在该实验平台上构建了同步电机的无源性控制系统,进行了空载实验。空载启动转速给定为1000r/min,图2为加减速过程,图3为电机转子位置。
由实验波形可知,采用无源性控制的电机能够较好的跟踪期望转速,稳态无静差;电机转子位置也能够实现快速跟踪。
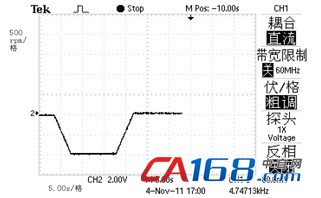
图2 电机转速波形
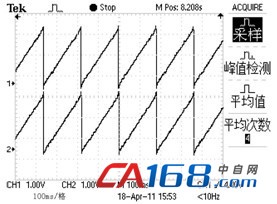
图3 转子位置波形
6结束语
本文从同步电机的E-L数学模型入手,考虑了转子阻尼绕组,通过选取合适的能量方程证明了电机系统是严格无源的;从机械和电气两方面考虑设计了磁链和转矩控制器,实现了气隙磁场定向的间接矢量控制。仿真结果验证了控制器的有效性。
实际上,同步电机功率因数也是控制系统的关键因素,而本文所设计的无源性控制器没有考虑这一因素。另外,系统中磁通控制是开环的,参数的变化或者磁路的饱和都可能使实际磁通偏离给定值,从而影响系统的控制性能。
作者简介
王利朋(1987-)男 硕士研究生,主要研究方向为电力系统。
参考文献
[1]陈峰, 徐立文. 基于无源性的同步电机控制器设计[J].电机与控制学报,1998,2(4): 217-220.
[2]薛花, 姜建国.同步电动机无源性控制方法[J].上海交通大学学报,2008,42(12): 2015-2019.
[3]马良河,姜建国.同步电动机任意设定转速的无源性跟踪控制[J].电工技术学报,2004,19(9): 37-41.
[4]张新华,戴先中.基于无源性的感应电机转矩与转速控制[J].电工技术学报,2001,16(4): 34-37.
[5]Romeo Ortega, Carlos Canudas, Seleme I. Seleme. Nonlinear control of induction motors: torque tracking with unknown load disturbance[J]. IEEE Transaction on Automatic Control, 1993: 1675-1680.
[6]陈伯时.电力拖动自动控制系统—运动控制系统[M].北京:机械工业出版社,2003.
[7]马良河.交流电动机的无源性传动控制研究[D].徐州:中国矿业大学,2004.
[8]李先允.现代控制理论基础[M].北京:机械工业出版社,2007.










共0条 [查看全部] 网友评论