1引言
异步电机是多变量、强耦合的非线性系统,因此要进行良好的转矩控制是非常困难的。现在异步电机之所以得到如此快的发展和普及,主要得益于矢量控制和直接转矩控制等控制技术的应用和不断完善。
现在异步电机矢量控制技术已经比较成熟,但矢量控制的控制结构比较复杂,而且需要复杂的坐标变换[1]。而异步电机直接转矩控制采用定子磁场定向无需解耦电流,直接控制电机的磁链和转矩,着眼于转矩的快速控制,以获得高效的控制性能[2]。但是由于常规的直接转矩控制方法采用滞环控制,因此存在转矩脉动大、开关频率不固定等问题。因此,为了提高异步电机驱动特性,近年来许多学者对此进行了深入的研究,提出多种解决方案,如使用空间矢量调制、预测控制以及人工智能控制的方法来保持恒定的开关频率。
本文首先建立了异步电机数学模型,阐述了SVPWM调制原理,在此基础上设计了一种基于模糊神经网络的磁链和转矩调节器,该调节器通过引入神经网络来解决先验知识不足时模糊规则的自确定问题,具有自适应、自学习能力、并且超调小,鲁棒性强等优点,从而实现良好的控制性能。最后通过仿真实验证明,采用该控制器的异步电机系统动态性能良好、低速脉动小。
2异步电机数学模型
异步电机的简化等效电路如图1所示。
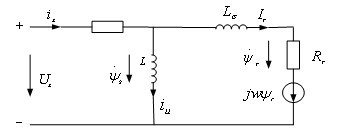
图1 异步电机简化图
根据上图可以推导出异步电机定子电压方程为:
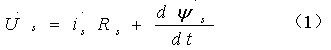
其中:Rs为定子电阻;Us、is、ψs分别为定子电压空间矢量、电流空间矢量、磁链空间矢量。
由此可以得到定子磁链方程为:
如果忽略定子电阻压降,将式(2)离散化为:
由上式得出,在△t时间内,定子磁链矢量的顶端沿电压矢量的方向移动。因此逆变器输出的离散电压直接控制定子磁链的幅值和相位,进而可以控制转矩。直接转矩控制的本质问题是在逆变器的各输出状态中选择合适的电压矢量,以达到控制目标。
异步电机的电磁转矩为[3]:
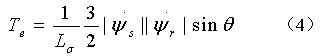
其中,ψr为转子磁链;θ为定子磁链与转子磁链之间的夹角,即磁通角。定子磁链∣ψs∣在控制中基本为常量,对转矩变化几乎没有影响。在异步电机运行过程中,转子磁链比定子磁链变化的慢,可以忽略转子磁链的动态特性。因此改变转子磁链和定子磁链之间的角度即可达到改变转矩的目的。
3异步电机直接转矩控制
空间电压矢量PWM控制是一种优化的PWM控制技术,典型的SVPWM实质是一种对在三相正弦波中注入了零序分量的调制波进行规则采样的一种变型SPWM[4]。相对于SPWM控制,SVPWM能明显减小逆变电路输出电流的谐波成分及电机的谐波损耗,降低转矩脉动,且其控制简单,数字化实现方便,电压利用率高,在交流伺服系统中得到越来越广泛的应用。
利用逆变电路功率开关管的开关状态和顺序组合,以及开关时间的调整,以保证电压空间矢量圆形运行轨迹为目标,就可以得到谐波含量小,直流电压利用率高的输出。三相逆变器共有000、001、010、 011、 100、 101、 110、 111等八种开关模式。其中000和111开关模式为零状态,此时电动机的定子磁链是不动的,则SVPWM的磁链轨迹如图2所示。
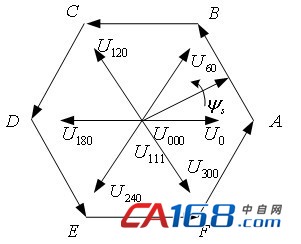
图2 SVPWM时序图
由图2可知,当逆变电路单独输出基本电压空间矢量Uo时,电动机的定子磁链矢量ψs的矢端从A到平行于Uo方向移动时,这样下去,当全部六个非零基本电压空间矢量分别以此单独输出时,定子磁链矢量ψs矢端的运动轨迹是一个正六边形。为获得圆形的旋转磁场,一种方法是利用六个非零矢量和两个零矢量的线性时间组合获得更多的开关状态。在每一个开关周期T期间,都改变相邻基本矢量作用的时间,并保证所合成的电压空间矢量的幅值都相等,因此当T取的足够小时,电压空间矢量的轨迹是一个近似圆形的正多边形。
直接转矩控制摒弃了矢量控制的解耦思想,从定子边入手,利用电机计算出的定子磁链和转矩,直接对他们进行控制,系统结构简单,易于实时控制,从而收到广泛的重视。与传统的直接转矩控制不同,本文设计的异步电机直接转矩控制系统采用模糊神经网络调节器对磁链和转矩进行控制,并采用SVPWM调制技术,以保证控制系统开关频率的稳定和逆变器高性能输出,则系统结构如图3所示。
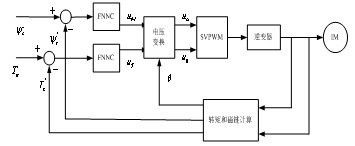
图3 直接转矩控制原理
系统通过采集逆变器输出端得三相电压和电流,通过磁通和转矩计算器估算出异步电机的磁链和转矩,然后和指令磁通和转矩进行比较得到误差。在定子磁链定向的同步旋转坐标系下,通过模糊神经网络调节器对磁通偏差、磁通偏差变化率、转矩偏差、转矩偏差变化率进行调节产生参考电压uM和uT,经过dq/αβ坐标变换可以得到二相静止坐标系下的电压矢量uα和uβ,即任意大小和相位的电压矢量。然后将获得的电压矢量作为逆变器输出电压矢量的参考值,再利用SVPWM技术进行矢量合成,将6个非零电压矢量和2个零电压矢量合成所需大小和相位的电压矢量,从而实现对异步电机磁链和转矩的直接控制。
4模糊神经网络控制器设计
模糊神经网络用反向传播算法调整模糊推理系统的隶属度函数参数,并能自动产生模糊规则,以解决模糊推理系统设计中隶属度函数确定的随意性和模糊规则提取难的问题。在控制应用时,不必进行复杂的规则搜索和推理,只需通过高速的并行分布式计算就可以产生输出结果[5]。
4.1模糊神经网络结构
本文设计的转矩和磁链模糊神经网络调节器采用相同的控制结构,该调节器原理如图4所示。
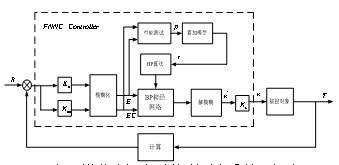
图4 模糊神经网络控制系统原理
其中:R为系统参考输入即转矩指令或磁链指令;ke、kec为量化因子、ku为比例因子;FNNC为模糊神经网络控制器;Y为系统的实际输出即逆变器输出的电压和电流。模糊神经网络调节器输入量为转矩误差或磁链误差、转矩误差变化率或磁链误差变化率;输出量为电压uM和uT。
模糊神经网络调节器利用异步电机模糊控制器输入/输出样本数据进行神经网络训练,自动产生模糊规则。样本数据和测试数据为模糊PI控制器的5000组输入/输出量进行归一化处理后的数据。为精确起见,我们将输入量和输出量在其论域内都划分为七个模糊子集{PB,PM,PS,O,NS,NM,NB}, 表示{“正大”,“正中”,“正小”,“零”,“负小”,“负中”,“负大”}。
神经网络结构采用简单的单隐含层BP网络。设Xk=[xik](i=1,2,3,…,n)为网络第k个输入的样本,则第j个隐含层神经元的输出zjk可表示为:
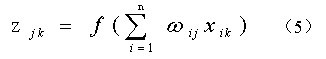
其中,ωij为第i个输入神经元和第j个隐含层神经元之间的连接权值,激励函数f(●)选用S型函数。
根据模糊子集划分可知输入层有14个节点,输出层有7个节点,根据Kolmogorov定理可得到隐含层有29个节点,网络训练采用弹性BP算法。神经网络训练完成后,通过对输出数据进行解模糊处理与比例因子相乘后获得实际输出电压uM和uT,然后进行电压空间矢量调制产生功率管驱动信号。
4.2网络训练
由于常规BP学习算法存在收敛速度慢和容易陷入局部极小值的问题。本文采用P A Mastorocostas提出的弹性BP算法对神经网络进行训练,这种算法不仅收敛速度快,而且解决了常规BP算法容易陷入局部极小值的问题,并且这种算法比较简单,也不需要消耗更多的内存空间。弹性BP算法的原理就是打算消除对偏导数的大小有害的影响权值,因此,惟有导数的符号被认为表示权更新的方向,而导数的大小对权值更新没有影响。权值改变量的大小仅由专门的“更新值”△i来确定。设网络的目标函数—全局误差为E:
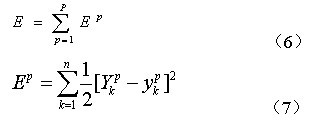
式中:P表示总样本,p表示第p个样本,k表示采样时刻,
表示k时刻网络输出和系统的实际输出。
弹性BP算法的具体编程步骤为:
设为前一时刻的误差梯度,η+、η-分别为增加和衰减因子。调节步长△i在[△max, △min]之间。则:
(1)初始化△i (1)= △0和连接权值Wi。
(2)提供训练样本,选择一对训练样本(Xp ,Tp)进行训练。
(3)输入模式进行正向传播过程计算。根据激励函数计算每一层的输出。
(4)误差的逆传播过程计算。从输出层向输入层反向计算各层神经元的一般化误差δ值,然后返回步骤(2)依次对P对训练样本进行计算。
(1)各层网络连接权值的修正计算。
(2)如果
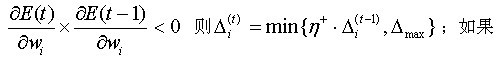
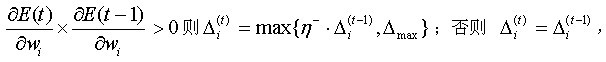
从而得到神经网络权值的修正值为:
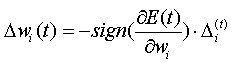
Wi(t+1)=Wi(t)+△Wi(t)
其中增长因子(6)返回(2),根据修正的网络连接权值对每一个学习样本返回步骤(2)重新计算,直到达到设定的网络目标函数—全局误差E<ε,或达到最大学习次数结束学习。
根据以上调整规则可以看出,如果前后两次的误差梯度的符号相同,则其参数的调整步长将增加,而与误差梯度的大小无关。通过这种方法调节参数,可以使得其变化步长在必需的时候增加,甚至到网络的最后学习阶段,即误差平面趋于平坦的时候也可能增加。当误差梯度的符号发生变化时,相应的调整步长将减小,可以有效防止振荡[6]。
5系统仿真
根据以上分析,在MATLAB/SIMULIN中建立系统仿真模型,其中异步电机参数如附表所示。
附表异步电机参数表
|
参数
|
值
|
参数
|
值
|
|
额定功率
(W)
|
1.5e5
|
定子电感(H)
|
0.3e-3
|
|
额定电压
(V)
|
380
|
转子电阻(Ω)
|
9.0 e-3
|
|
频率
(Hz)
|
50
|
转子电感(H)
|
0.3 e-3
|
|
极对数
|
2
|
互感
(H)
|
1.0 e-4
|
|
定子电阻
(Ω)
|
0.015
|
转动惯量(kg. m²)
|
3
|
设定系统在时刻[0 1]速度为[500 0] r/min ;并在时刻 [0 0.5 1.5] 系统加 [0 800 -800] Nm的负载。异步电机直接转矩控制系统分别采用传统PI控制和模糊神经网络控制的转矩和转速的仿真结果如图5和图6所示(1为参考信号,2为实际信号)。
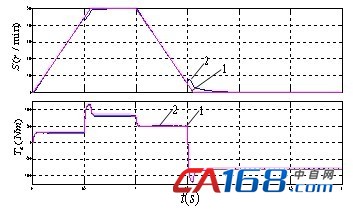
图5 PI控制的电机转速和转矩仿真效果
由图5可以看出基于常规的PI控制的异步电机直接转矩控制可以获得较好的控制效果。但是其在低速运行时脉动较大,并且在负载突加或突减时转矩波动较为明显。
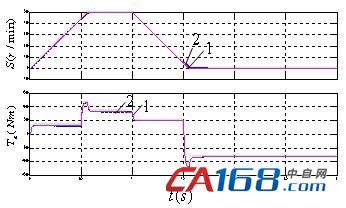
图6 FNN控制的电机转速和转矩仿真效果
由图6可以看出,本文提出的基于模糊神经网络的异步电机直接转矩控制方法无论在正常运行情况下,还是在负载突加或突减的情况下,都可以很好的跟踪参考转速和转矩信号,并且较好的改善了异步电机低速脉动问题。
5结束语
仿真结果表明,本文提出基于模糊神经网络的异步电机直接转矩控制无论在正常情况下,还是在负载突变情况下,都可以保持良好的动、静态性能,说明了该算法的正确性和可行性。尤其在低速时能够利用模糊神经网络的自学习能力自适应异步电机的动态变化,转矩脉动较小,因此具有一定的实际应用价值。
作者简介
徐保友(1984-)男 硕士研究生,研究方向为电气传动与控制技术。
参考文献
[1]马小亮.矢量控制系统中异步电动机参数的估算和测量[J].电气传动,2010,26(30):3-7.
[2]杨俊华,吕惠子,吴捷等.基于波波夫超稳定性的无刷双馈电机直接转矩控制[J].中国电机工程学报,2009,15(29):107-113.
[3]孙笑辉,张增科,韩曾晋等.基于直接转矩控制的感应电动机转矩脉动最小化方法研究[J].中国电机工程学报,2002,22(8):109-112.
[4]马丰民,吴正国,侯新国等.基于统一PWM调制器的随机空间矢量调制[J].中国电机工程学报,2007,7(27):98-102.
[5]曹先庆,朱建光,唐任远等.基于模糊神经网络的永磁同步电动机矢量控制系统[J].中国电机工程学报,2006,1(26):137-141.
[6] Mastorocostas P A. Resilient back propagation learning algo2rithmfor recurrent fuzzy neural networks [J].Electronics Let2ters ,8th January 2004 ,40 (1) :27 - 31.





共0条 [查看全部] 网友评论