1引言
空间矢量调制（SVM）技术在交流传动系统中得到了广泛的应用，与传统的正弦脉宽调制（SPWM）相比，SVM的线性调制范围更宽，直流母线利用率高，输出电压谐波小，是一种很有实用价值的PWM控制方法。
SVM有多种数字化实现方法，本文在分析SVM基本原理的基础上，采用一种比较简单的数字化方法，以dsPIC30F单片机为控制芯片，实现了SVM输出，并给出了相应的实验结果。
2SVM的基本原理
以三相电压源型逆变器（VSI）为例来分析SVM的基本原理，三相VSI的拓扑结构如图1所示。
对于三相VSI而言，负载的相电压依赖于所对应的桥臂开关管的状态，由于每相桥臂上下两个开关管互补通断，因此其输出共有23=8种状态。
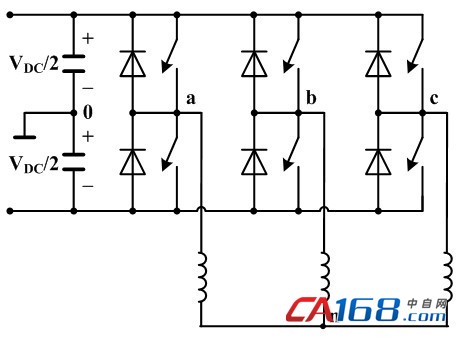
图1 三相VSI典型结构
根据空间矢量的基本概念，得三相VSI电压空间矢量：
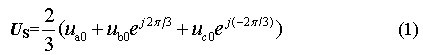
根据公式（1），可得与8种输出状态相对应的8个电压空间矢量U0，U1，…，U7，如图2所示。其中U1~U6为6个有效电压空间矢量，U0与U7为零矢量，6个有效电压空间矢量的幅值相等，均为2VDC/3（VDC为逆变器直流母线的电压），相位上互差π/3电角度。
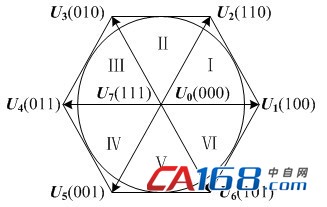
图2 三相VSI的电压空间矢量
采用SVM控制的目的是产生圆形旋转磁场，而对于三相VSI而言，只有6个有效的电压空间矢量和2个零矢量，仅用这8个电压矢量显然达不到控制要求，因此要利用其中的几个矢量去合成所需要的电压空间矢量，使所形成的实际的磁链矢量来追踪标准的磁链圆。实际上，根据所期望的电压空间矢量所在的扇区，可以用相邻的2个电压空间矢量及零矢量来合成，如图3所示，假设所期望的空间矢量位于扇区Ⅰ。
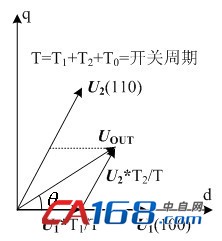
图3 空间矢量合成
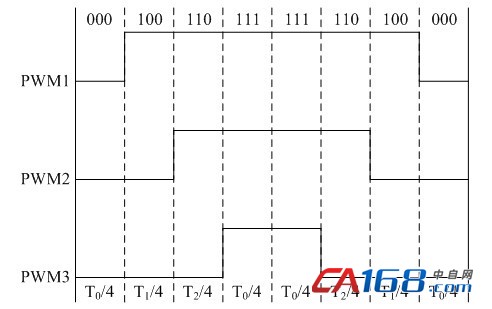
图4 扇区Ⅰ开关顺序
根据伏秒平衡原理，得：
UoutT=U1T1+U2T2 ，即：Uout= U1T1/T+ U2T2/T
其中T1、T2分别为矢量U1、U2的作用时间，T为开关周期，零矢量作用时间：T0=T–T1–T2，开关顺序如图4所示[1]。
规定、、分别表示矢量Uout 、U1、 U2的幅值且U1= U2=2VDC/3，由三角形正弦定理，得：
则Uout的最大值为
恰为图2中正六边形内切圆的半径，这也是SVM在线性控制区所能输出的最大相电压[2]，如果超过这个值，输出电压波形会产生失真。
而对于三相VSI，若采用普通规则采样SPWM控制方式，在线性控制区逆变器所能输出的最大相电压为VDC/2，SPWM的最大线性调制比为1，则SVM的最大线性调制比为SPWM的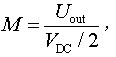
倍，即SVM最大线性调制比可达1.15，提高了约15%[3]。实际上，与SPWM类似，定义调制比
以直流母线中点为参考点，可得SVM相参考电压（平均值）解析表达式[4]，以a相为例：
相电压Va0（平均值）的最大值为VDC/2，则调制比M的范围：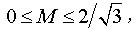
根据以上表达式，可以得到a相电压（平均值）的波形，如图5所示，取调制比
根据文献[4]，该平均电压可以认为由两个分量构成，一个分量是该相到负载中性点的正弦电压，并且当
时，该正弦电压的峰值可达
根据以上表达式，可以得到a相电压（平均值）的波形，如图5所示，取调制比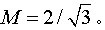根据文献[4]，该平均电压可以认为由两个分量构成，一个分量是该相到负载中性点的正弦电压，并且当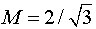时，该正弦电压的峰值可达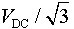另一个分量是负载中性点与直流母线中点间的三倍于基波频率的三角形电压，因此，SVM与三次谐波注入SPWM有类似之处。
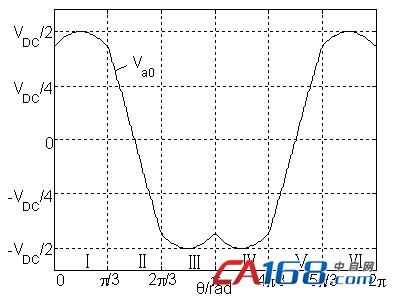
图5 a相参考电压（平均值）波形
3SVM的数字实现方法
SVM的数字实现方法多种多样，本文采用一种比较简单的实现方法，并重点从软件编程方法的角度来分析。单片机采用Microchip公司的电机与电源系列数字信号控制器dsPIC30F4011，该单片机具有专门的电机控制PWM（MCPWM）模块，PWM模块具有3个占空比寄存器PDC1、PDC2、PDC3，可以产生6路输出，每个输出引脚均可互补或独立工作；具有用于互补模式的硬件死区时间发生器[5]；在PWM中断中改变3个占空比寄存器的值，可以很方便地产生所需的PWM波。
软件编程的关键是要确定2个有效电压矢量作用时间T1、T2以及零矢量作用时间T0，以此来确定占空比寄存器PDC1、PDC2、PDC3的值。如前文所述，根据公式（2）、（3），令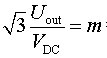
得：
T1=mTsin（60°-θ）
T2=mTsinθ
以上两式就是软件实现SVM所采用的算法，需要说明的是，无论目标电压矢量位于哪个扇区，该算法都是适用的，只需将θ视为目标电压矢量与其所在扇区电压矢量的夹角，即若目标电压矢量位于图2中第i(i=1~6)扇区，则θ为目标电压矢量与有效电压矢量Ui的夹角。
6个有效电压空间矢量将整个圆周6等分，程序中用16位的常量来表示0°、120°、180°等电角度，如0x0000表示0°，0x2AAA表示60°，0x5555表示120°，依此类推。以这些常量值作为6个扇区的边界，以判断目标电压矢量所在扇区，同时进行θ角的计算。本文针对开环控制方式来说明扇区判断方法，电压空间矢量在六个扇区内匀速旋转，每个扇区对应输出电压基波周期的，可以将每个扇区n等分，每一等份对应时间△t=1/6nfbase（fbase为基波频率），每经过△t时间，电压空间矢量转过△θ电角度，程序中将△θ作为一个增量值，每次PWM中断将△θ累加，将累加值与各个扇区的边界值作比较，以判断电压空间矢量所在扇区。
为了计算T1、T2，程序中建立一个60°的正弦表，利用查表法获得sin（60°-θ）以及sinθ值，以提高程序的执行效率；可以将m视为另一种定义方式下的“调制系数”，在开关周期确定的情况下，就可以计算出T1、T2的值，然后给占空比寄存器赋予相应的值。举例来说，目标电压矢量位于扇区Ⅰ，则三个占空比寄存器的值依次为：PDC1=T1+T2+T0/2，PDC3 T0/2，其他五个扇区可以根据相应的开关顺序来确定三个占空比寄存器值的计算公式。
4实验结果
程序中设定开关频率为3kHz，基波频率为50Hz，实验结果如图6、图7所示。图6（a）、（b）均为逆变器PWM电压波形，开关频率为3kHz，（b）图为局部放大的结果，从中可以看出PWM波占空比的变化过程。图7为所输出PWM波的低频成分，频率为50Hz，与图5中的理论分析波形相比较，二者在形状上是基本吻合的，这也说明了实验结果的正确性。
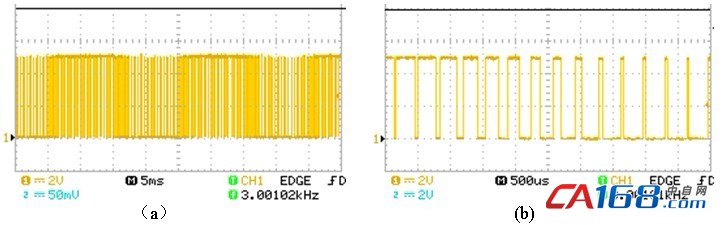
图6 逆变器PWM波形
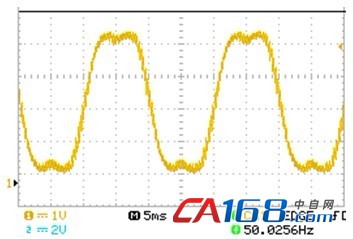
图7 逆变器PWM波的低频成分
5结束语
SVM以产生圆形旋转磁场为目的，利用6个有效电压空间矢量来合成目标电压空间矢量；SVM的最大线性调制比可达1.15，与SPWM相比，提高了直流母线电压利用率。SVM可以方便地利用单片机进行数字化实现，从实验结果来看，所用方法是合理和正确的。
作者简介
于洋（1987-）男 硕士研究生在读，研究方向为电力电子与电力传动。
张加胜（1957-）男 教授、博士生导师，研究方向为电力电子与电力传动。
参考文献
[1]Dave Ross, John Theys, Steve Bowling．Using the dsPIC30F for Vector Control of an ACIM. Microchip Technology Inc, 2007．
[2]杨贵杰，孙力．空间矢量脉宽调制方法的研究[J]．中国电机工程学报，2001，2l(5)：79-83．
[3]H. W. Van Der Broeck, H .C. Skudelny , G. Stanke. Analysis and Realization of a Pulse Width Modulator Based on Voltage Space Vectors. IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, 1988, 24(1):142-150．
[4]D.G.Holmes,T.A.Lipo.Pulse Width Modulation for Power Converters: Principles and Practice. New Jersey: Wiley-IEEE Press, 2003:259-336．
[5]Microchip.dsPIC30F4011/4012 Data Sheet.Microchip Technology Inc, 2008．
共0条 [查看全部] 网友评论