基于欧姆龙NJ控制器的半自动芯片封装机
发布日期:2012-11-13 浏览次数:49725
【摘 要】:1 引言 半导体制造技术接近突破摩尔定律的飞速发展,推动半导体产业分工在全球区域重新分配,半导体芯片封装测试流程业务外包已
6.2 数学建模方案
(1)方案:通过数学建模得出伺服位置和台面位置之间的关系。正向求解较为麻烦需要准确测量各个力臂长度和角度等关系。所以选择测点反推公式的方法,现场测量伺服位置和台面位置关系点上百个,通过数学建模软件得到近似公式。根据实际精度要求和PLC计算能力选择几阶方程,选择四几阶方程得到的表达式为
实轴到虚轴的关系(公式1)
Y=5.83991*10-8*X4-2.89331*10-5*X3+1.13492*10-3*X2+1.3258*X-1.9369
虚轴到实轴的关系(公式2)
Y=7.16569*10-7*X4-1.95228*10-4*X3+0.0179*X2+0.21282*X+4.24585
(2)分析:伺服电机位置通过公式1换算成台面位置显示给客户看,客户设定值通过公式2转换为伺服应该走的目标位置。通过这种方式存在误差,1:公式是近似的,且存在常数项即X=0时Y<>0。2:通过两次计算误差叠加。客户设定位置X通过公式2换算成伺服电机目标位置Y,伺服电机准确定位到达位置Y,位置Y通过公式1换算成台面位置Y’显示给客户,但是因为公式存在误差导致Y<> Y’。现场调试发现误差最大达到3-4mm。
6.3 凸轮查表方案
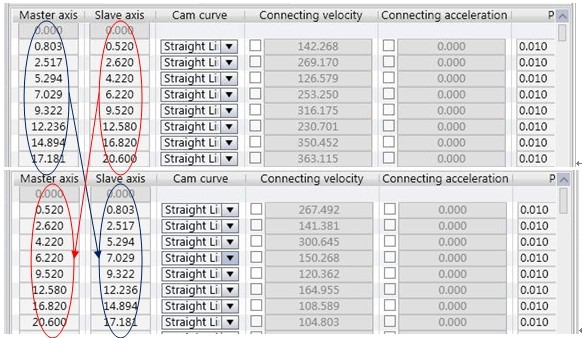
尽管电子凸轮应用在这种场合存在局限,但是受到凸轮表生成曲线坐标点的原理启发,本案通过凸轮表生成精确的表格,然后通过查表方式实现位置修正。建立两张互逆凸轮表,phase pitch为0.01(修正精度为0.01mm)。通过查表方式实现转换。 修正后值:= (Cam0[修正前值*100].Distance) :
6.2 数学建模方案
(1)方案:通过数学建模得出伺服位置和台面位置之间的关系。正向求解较为麻烦需要准确测量各个力臂长度和角度等关系。所以选择测点反推公式的方法,现场测量伺服位置和台面位置关系点上百个,通过数学建模软件得到近似公式。根据实际精度要求和PLC计算能力选择几阶方程,选择四几阶方程得到的表达式为
实轴到虚轴的关系(公式1)
Y=5.83991*10-8*X4-2.89331*10-5*X3+1.13492*10-3*X2+1.3258*X-1.9369
虚轴到实轴的关系(公式2)
Y=7.16569*10-7*X4-1.95228*10-4*X3+0.0179*X2+0.21282*X+4.24585
(2)分析:伺服电机位置通过公式1换算成台面位置显示给客户看,客户设定值通过公式2转换为伺服应该走的目标位置。通过这种方式存在误差,1:公式是近似的,且存在常数项即X=0时Y<>0。2:通过两次计算误差叠加。客户设定位置X通过公式2换算成伺服电机目标位置Y,伺服电机准确定位到达位置Y,位置Y通过公式1换算成台面位置Y’显示给客户,但是因为公式存在误差导致Y<> Y’。现场调试发现误差最大达到3-4mm。
6.3 凸轮查表方案
尽管电子凸轮应用在这种场合存在局限,但是受到凸轮表生成曲线坐标点的原理启发,本案通过凸轮表生成精确的表格,然后通过查表方式实现位置修正。建立两张互逆凸轮表,phase pitch为0.01(修正精度为0.01mm)。通过查表方式实现转换。 修正后值:= (Cam0[修正前值*100].Distance) :

导出的凸轮表数据如下:如果当前台面位置为0.1根据上面公式可以得到伺服位置应该为:0.0648 =(Cam0[0.1*100].Distance)即是凸轮表第十行主轴数据。以此类推很容易查到根据凸轮关系得到的转换位置。
7 结束语
基于欧姆龙NJ系列高性能多功能一体化控制器的半自动芯片封装机已经现场调试成功。现场压力控制顺利实现。在压力控制过程中,尽管转矩瞬时超载高达200%,但由于时间控制未导致伺服过载。注塑压力到达后采用抱闸保压,合模压力抱闸稳定度达到工艺要求。机械传动非线性通过凸轮查表方案实现高精度线性化伺服跟踪定位,大幅度提升装备易用性。
7 结束语
基于欧姆龙NJ系列高性能多功能一体化控制器的半自动芯片封装机已经现场调试成功。现场压力控制顺利实现。在压力控制过程中,尽管转矩瞬时超载高达200%,但由于时间控制未导致伺服过载。注塑压力到达后采用抱闸保压,合模压力抱闸稳定度达到工艺要求。机械传动非线性通过凸轮查表方案实现高精度线性化伺服跟踪定位,大幅度提升装备易用性。







共0条 [查看全部] 网友评论