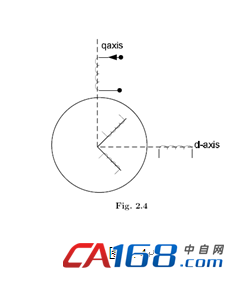
首先考虑两相异步电机的动态模型,然后推导出两相与三相电机间的等效模型。两相异步电机定子绕组为两组,彼此成90度角的空间排布。异步电机的转子也可等效为两相绕组,如图2.4所示。定子绕组位于d轴及q轴上,转子绕组则分布于α和β轴上。在任意时刻,转子绕组α与定子绕组d间的夹角为θ。定子及转子绕组的终端电压,可以表示为由于内阻及磁通变化所产生的压降之和。其中,磁通变化量由电流及电感量(包括自感及互感)的变化引起。对于两相异步电机而言,其内部四个绕组(回路)每一回路内均要考虑其自感系数及互感系数。d、q、α及β四个回路,其自感系数均包含主磁通及漏磁磁通分量,且均与转子位置无关。
以上自感量有如下关系式


以上自感量有如下关系式

定子绕组d和q,以及转子绕组α和β间的互感系数(互感量)均为零,因为它们之间均为90度夹角。
因此还有


而定子绕组与转子绕组间的互感系数则与转子角度θr 存在函数关系。由于气隙间的磁动势成正弦曲线分布,因此互感系数与角度θr 间成余弦函数关系。假设此处角度θr 为转子α与定子d轴间的电气夹角。
则有
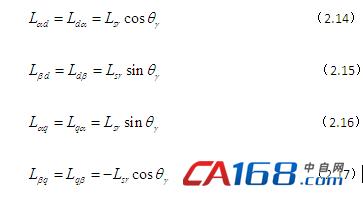
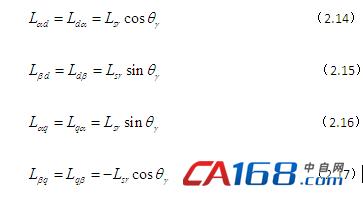
式中,Lsr为转子绕组与定子绕组间互感系数最大值。
Vds、Vqs、Vα以及Vβ分别为定子绕组d和q轴上的端电压,及其对应绕组α和β两端电压,而每相的相间电流分别为:ids 、iqs 、iα和iβ。依据压降与磁通量变化间的电压方程式如下所示。
即
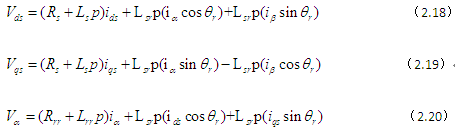
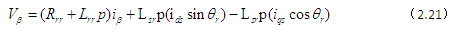
式中,定子绕组阻抗表示为式(2.22)

转子阻抗为

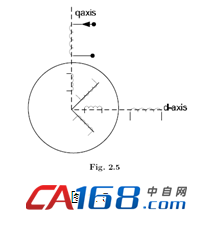
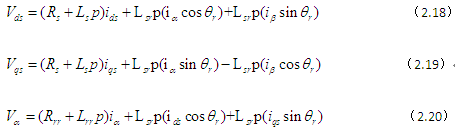
式中,定子绕组阻抗表示为式(2.22)
转子阻抗为
考虑到电感量与转子位置间的函数关系,由以上方程式(2.18 ~ 2.21)的解较为复杂,而用常数取代电感量的变换则可将方程式简化。
2.3.1 通过变换获得恒定的电感
为了将随时间变化的电感量替换为恒定电感值,需要引入数学变换将方程式内cosθr 和sinθr 移除。针对感应式电机的电压方程式,H.C. Stanley在20世纪三十年代提出了由于电流回路相对运动而产生的电感变化,可以通过将转子变量转换为假想的固定绕组变量予以消除。为实现该变换,假设转子绕组在d轴及q轴上相对定子固定(如图2.5),以上假定绕组同实际转子绕组一样具有相同的匝数因此产生相等的磁动势。若假想绕组电流为iqrr 及irdr ,则可用通过以下等式进行变换。
即
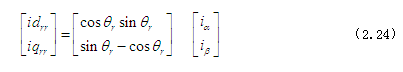
带入以上值,电压方程式(2.18~2.21)可转化为以下方程

式中,ω = dθr / dt ,则等式(2.25)中电感值转化为恒定常数。
然而,通常为了获得稳态方程式才会将转子变量相对定子进行变换。如果转子端电压与定子侧相等,转子和定子绕组事实上可以物理连接。由于假想绕组特性需要与实际转子绕组的特性相同,因此以下参数变换是必须的。
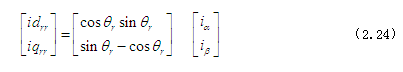
带入以上值,电压方程式(2.18~2.21)可转化为以下方程

式中,ω = dθr / dt ,则等式(2.25)中电感值转化为恒定常数。
然而,通常为了获得稳态方程式才会将转子变量相对定子进行变换。如果转子端电压与定子侧相等,转子和定子绕组事实上可以物理连接。由于假想绕组特性需要与实际转子绕组的特性相同,因此以下参数变换是必须的。

如果
a = 定子每相匝数/转子每相匝数 (2.26)
则相应变量如下
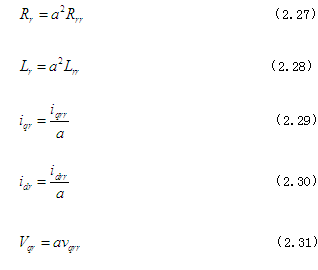

因此,定子的磁化电感与互感间现在具有如下关系式

将式(2.27~2.33)中变量代入式(2.25)中,得到简化后的两相电机动态方程如下。
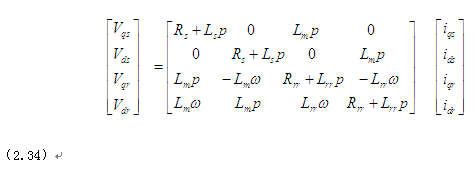
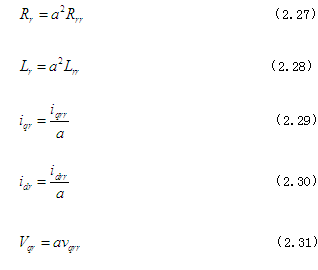
因此,定子的磁化电感与互感间现在具有如下关系式
将式(2.27~2.33)中变量代入式(2.25)中,得到简化后的两相电机动态方程如下。
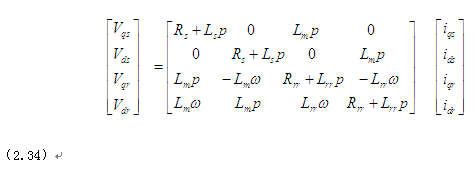
以上方程表现的阻抗特性,主要取决于转子速度。若转子转速恒定,则电机处于稳态且以上方程式(2.34)为线性等式。
2.3.2 三相电动机的动态模型
两相电机的动态模型如上一节中的方程式(2.34)所示。然而,相比两相电机,三相异步电机在工业领域内的应用更为广泛。通过坐标轴变换可将三相电机表示为其等效的两相电机,如下图2.6所示。其中,ds 及qs 为定子正交轴,dr 及qr 为转子正交轴。
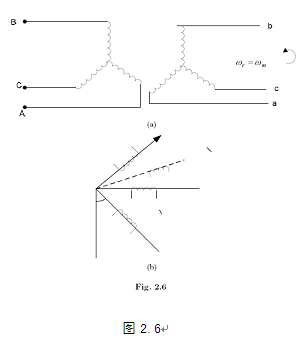
通过坐标轴变换,将a - b - c端电压/电流转化为d - q - o端的电压/电流。该变换将电压,电流及磁通量与定子绕组相关联,进而在d轴及q轴上将各实际转子变量与假想转子绕组相关联,该假设由R. H. Park在二十世纪二十年代首先提出。通过以上变换(Park变换)可消除时变电感量对等式的影响。如果qs 轴滞后a轴的角度为θc ,则通过Park变换,d - q - o轴上的电流与a - b - c轴上的电流具有如下关系:上标s表示d - q - o轴位于定子上。
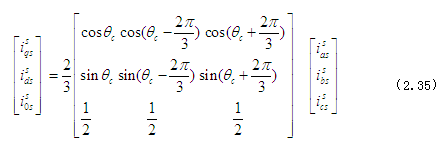

通过坐标轴变换,将a - b - c端电压/电流转化为d - q - o端的电压/电流。该变换将电压,电流及磁通量与定子绕组相关联,进而在d轴及q轴上将各实际转子变量与假想转子绕组相关联,该假设由R. H. Park在二十世纪二十年代首先提出。通过以上变换(Park变换)可消除时变电感量对等式的影响。如果qs 轴滞后a轴的角度为θc ,则通过Park变换,d - q - o轴上的电流与a - b - c轴上的电流具有如下关系:上标s表示d - q - o轴位于定子上。
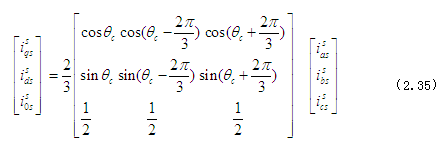
注意,仅当a - b - c相间存在电流不平衡时,才会出现电流io ,由此并不会减弱感生磁场强度。
方程式(2.33)可以简化为以下形式

同样,可通过Park变换的逆变换,由iqdo 求得iabc 。

式中
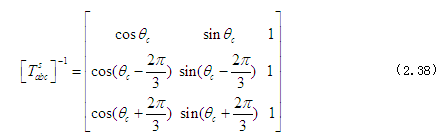
同样,可通过Park变换的逆变换,由iqdo 求得iabc 。
式中
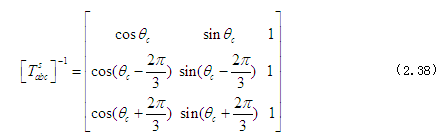
以上变换方法同样适用于计算电压及磁通量。若滞后角度θc 为0 ,则qs 轴与a轴重合且系统处于平衡态(无中性点联接),则系统仅表现为d轴和q轴。相应变换可表示为如下等式。
即

对于平衡态三相系统则有
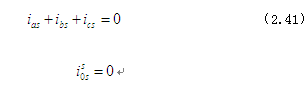
以及
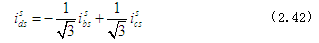
以磁通量表示的电压方程式如等式(2.34)。通过以上方程,对于平衡态的系统而言,可建立两相异步电机与三相异步电机之间的等值关系。但是,如果系统不在平衡态,则等式(2.34)中会相应增加以下两个部分。

式中,Lls 以及Llr 分别为定子和转子的漏感。

对于平衡态三相系统则有
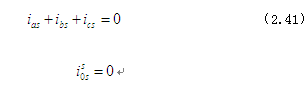
以及
以磁通量表示的电压方程式如等式(2.34)。通过以上方程,对于平衡态的系统而言,可建立两相异步电机与三相异步电机之间的等值关系。但是,如果系统不在平衡态,则等式(2.34)中会相应增加以下两个部分。

式中,Lls 以及Llr 分别为定子和转子的漏感。









共0条 [查看全部] 网友评论