1 引言

柴油机作为动力设备已广泛应用到社会生产的各个场合，如石油勘探、工程机械、矿山开采等领域。然而由于柴油机结构复杂和工作环境恶劣，其故障发生可能性较大。若故障发生，不仅会直接影响到整个系统的正常运行，严重时还造成经济损失和人员伤亡^[1-2]。因此，对其进行有效地故障诊断以便及时做出处理显得尤为重要。

支持向量机（Support Vector Machines, SVM）是以统计学习理论为基础，针对有限样本的一种通用学习方法，能有效解决小样本、高维数、非线性等问题，并克服了神经网络学习方法中网络结构难以确定、收敛速度慢、局部极小点、过学习与欠学习以及训练时需要大量数据样本等不足，具有良好的推广性能^[3-5]。然而在解决实际问题时，支持向量机核函数参数和惩罚因子的选择却会直接影响到其分类性能的好坏。基于此，提出一种基于差分进化算法优化支持向量机参数来进行柴油机故障识别的方法，以期能够获得较高的故障识别率，进而能够正确判断故障类型，便于采取有效处理措施保证系统正常运转。

2 差分进化算法

2.1 差分进化算法简述

差分进化算法过程主要有交叉、变异、选择三部分组成，具体实现步骤如下：

（2）变异操作。在该算法中，常用的变异方式有DE/rand/1/bin和DE/best/1/bin两种，为提高求解速度、加快收敛，在此选择用DE/best/1/bin 变异形式：

（5）终止判断。如果达到最大迭代次数抑或满足要求的精度，则停止运算并输出最优结果，否则返回2）继续。

2.3 基于差分进化算法优化支持向量机的参数选择

Vapnik等已通过研究证明，支持向量机核函数选择的不同对其分类性能影响较小，因此，本文直接选择用RBF径向基函数作为核函数。利用差分进化算法对对支持向量机惩罚因子C和核函数参数σ进行选择时，应对该算法的一些相关参数和适应度函数进行如下设置：

（1）初始化差分算法中的控制参数。如：初始种群数量SN，优化参数数量D，最大循环次数maxcycle。

（2）设置适应度函数。对支持向量机参数进行优化的目的是为了能够最大程度的获得较高的分类正确率，因此，将适应度函数设置为：

（3）初始化支持向量机参数的搜索范围。由于支持向量机惩罚因子和核函数参数的不同取值会影响到最后分类结果的好坏，因此，应当确定合适的搜索范围以有助于分类正确率的提高。

3 柴油机故障诊断

3.1 实验方案设计

实验对象是某12缸柴油机，故障设置为G1—右6缸断油、G2—左1缸断油、G3—左1缸和右6缸双缸断油、故障G4—左1缸喷油泵渗漏、故障G5—空气滤清器堵塞；信号采集装置有压电式加速度传感器、电荷放大器、DASP数据采集仪及笔记本电脑等；实验中采集正常状态、故障G1、故障G2、故障G3、故障G4和故障G5六种情况下柴油机转速1500r/min、采样频率40kHz右3缸缸体处的振动信号数据，提取每种工况下样本各6组。

3.2 信号分析与特征值提取

对采集到的振动信号进行降噪后，为便于后续故障识别工作的顺利进行，应对振动信号进行特征值提取。由于小波包分析法对于振动信号无论在低频段或是高频段分解的效果都比较好，因此，利用“db1”小波基函数对信号小波包分解并提取能量特征，其步骤如下：

（1）进行信号小波包分解。把降噪后的信号进行3层小波包分解，并提取第3层从低到高共8个频率段的信号X3j，其中j（j=0,1,2,3…8）为节点数。

（2）重构小波包分解系数。对第3层的所有节点进行小波包重构，并用S3j表示重构后的信号，则重构后总信号可表示为S=S30+S31+S32+…+S37。

（3）求解各频带信号能量。设S3j的能量为E3j，j=0,1,2,3…7。

（4）构造特征向量。将第3节点各频段的能量值取为特征向量T0，则有T0=[E30，E31，E32…E37]。

（5）进行归一化处理。为避免由于E3j较大而带来后续数据处理不便的影响，应对T0进行归一化处理得T1，即T1=[E30/E,E31/E,E32/E…E37/E]。

信号经3层小波包分解可以得到8个频带，同时得到8个特征值，如表1所示。图1显示的是六种工况下各一组振动信号数据经过特征值提取后所对应的能量谱图。

表1 频段与故障特征值

频段	特征值
1	T1(E30/E)
2	T2(E31/E)
3	T3(E32/E)
4	T4(E33/E)
5	T5(E34/E)
6	T6(E35/E)
7	T7(E36/E)
8	T8(E37/E)

 

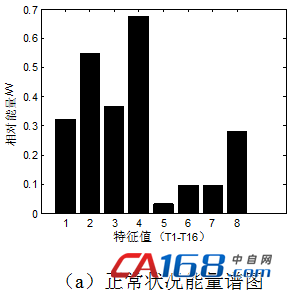
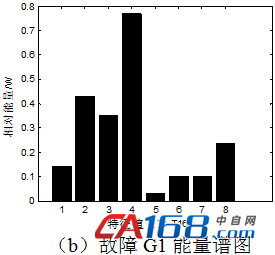
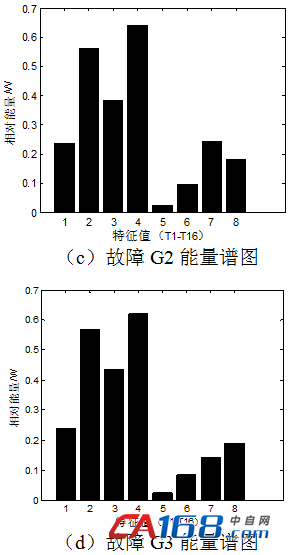
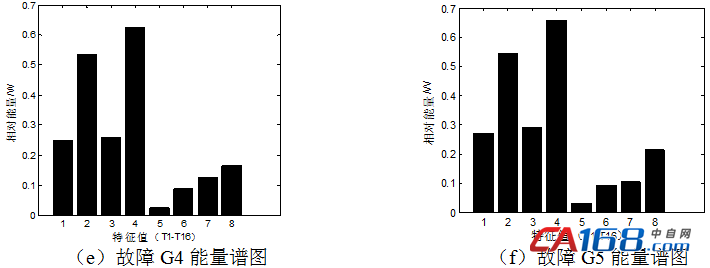
图1 六种工况下小波包分解后的能量谱图

 

4 柴油机故障识别

4.1 获取诊断样本数据

实验时每种工况下的柴油机振动信号采集6次，因此，经小波包能量谱特征值提取后可以得到36个样本数据，在故障诊断中，将每种工况的前3个样本作为训练样本，后3个样本作为测试样本，即六种工况下最终的训练样本与测试样本数各18个，其中正常状况、故障G1和故障G5的训练样本与测试样本分别参见表2和表3所示。

 

表2 训练样本

工况	序号	T1	T2	T3	T4	T5	T6	T7	T8
正常状况	1	0.3106	0.5739	0.3757	0.6149	0.0347	0.0900	0.1087	0.1838
	2	0.3236	0.5499	0.3647	0.6763	0.0336	0.0956	0.0958	0.2801
	3	0.3404	0.5788	0.3716	0.5913	0.0239	0.0833	0.0908	0.2053
故障G1	1	0.1803	0.4638	0.3399	0.7415	0.0313	0.0893	0.1644	0.2259
	2	0.1425	0.4322	0.3527	0.7689	0.0317	0.1011	0.1001	0.2367
	3	0.1608	0.4720	0.3058	0.7688	0.0274	0.1037	0.1365	0.2618
故障G5	1	0.2639	0.5587	0.2745	0.7026	0.0285	0.1002	0.0965	0.1702
	2	0.2702	0.5457	0.2898	0.6586	0.0313	0.0930	0.1034	0.2137
	3	0.2627	0.598	0.3033	0.6400	0.0316	0.0931	0.1285	0.1629

 

表3 测试样本

工况	序号	T1	T2	T3	T4	T5	T6	T7	T8
正常状况	1	0.3120	0.5505	0.3436	0.6600	0.0257	0.0959	0.1131	0.1866
	2	0.3625	0.6291	0.3262	0.6581	0.0244	0.0926	0.1228	0.1634
	3	0.3594	0.6455	0.3554	0.6382	0.0269	0.0982	0.0792	0.1802
故障G1	1	0.1599	0.4874	0.3049	0.7586	0.0260	0.0961	0.1063	0.2886
	2	0.1694	0.4621	0.3021	0.7486	0.0267	0.0938	0.1591	0.2631
	3	0.1678	0.4535	0.283	0.7350	0.0282	0.1037	0.1163	0.2729
故障G5	1	0.2188	0.5896	0.2739	0.6782	0.027	0.0847	0.1496	0.1982
	2	0.2104	0.5986	0.2946	0.7384	0.0306	0.0882	0.1191	0.2284
	3	0.2151	0.5183	0.2674	0.7493	0.0274	0.1105	0.0807	0.1806

 

4.2 未优化的支持向量机故障识别

将训练样本与测试样本输入到参数为优化的支持向量机中进行故障诊断，其结果如图2所示，不同参数取值对应的各类工况的分类正确率如表4所示。

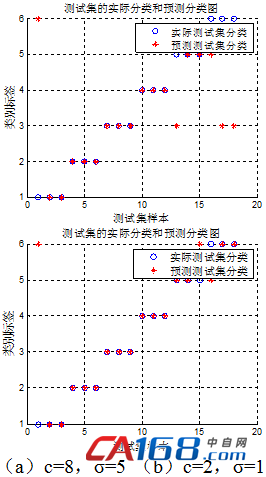
图2 参数未优化的支持向量机故障分类图

 

表4 故障分类正确率

参数值	正常	故障G1	故障G2	故障G3	故障G4	故障G5	总识别率
c=8，σ=5	66.67%	100%	100%	100%	66.67%	0	72.22%
c=2，σ=1	66.67%	100%	100%	100%	66.67%	66.67%	83.33%

 

4.3 差分进化算法优化支持向量机用于故障识别

设置种群数量SN=20，最大循环次数maxcycle=50，支持向量机参数搜索范围为[0.1 50]，将优化后的支持向量机进行故障诊断，其分类结果如图3所示，得到最优参数值为惩罚因子c=11.9561，核函数参数σ=0.1。各工况分类正确率及运行时间如表5所示。

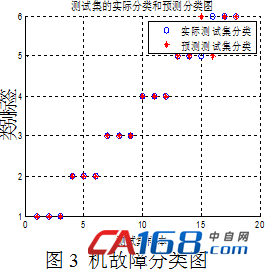
表5 差分进化算法优化支持向量机的故障分类正确率及运行时间

参数值	正常	故障G1	故障G2	故障G3	故障G4	故障G5	总识别率	运行时间
c=11.9561 σ=0.1	100%	100%	100%	100%	66.67%	66.67%	88.89%	3.229s

 

5 结束语

支持向量机是进行柴油故障识别的一种重要工具，然而其核函数参数和惩罚因子选择的好坏关系到其能否获得较高的分类正确率。为克服这一问题，利用差分进化算法优化支持向量机相关参数，并通过柴油机故障诊断试验，进一步证明该方法能够在较短时间内获得较高的故障分类正确率，即说明该方法对于柴油机故障诊断具有重要的应用价值。

参考文献

[1]马善伟,乐正伟,吕健等.柴油机故障诊断技术综述[J].上海第二工业大学学报,2008,25(2):122-128.

[2]陈鹏,陈晓宁,王征.现代柴油机故障诊断方法发展[J].机电技术,2014(6):154-156.

[3]曲志刚,封皓,靳世久.基于支持向量机的油气管道安全监测信号识别方法[J].天津大学学报,2009,42(5):465-470.

[4] CRISTIANINI N,et al.An introduction to support vector machines and other kernel-based learning methods [M].Beijing, Mechanical industry press,2005.

[5] 杨志民,刘广利.不确定性支持向量机原理及应用[M].北京:科学出版社,2007.

[6] Storn R,Price K.Differential evolution—A simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkeley:University of California.2006.

[7]贾东立,郑国莘.基于混沌和高斯局部优化的混合差分进化算法[J].控制与决策,2010,25(6):899-902.

[8]周智成.基于改进人工蜂群算法的输电网扩展规划研究[D].广西大学,2014.

[9]康忠健,訾淑伟.基于差分进化算法的油田区域配电网无功优化技术的研究[J].电工技术学报,2013,28(6):226-231.

[10]胡超杰.差分进化算法及其在电机参数辨识中的应用研究[D].湖南大学,2013.