1  引言

在电动机车牵引领域，受到变流器体积与散热能力的限制，功率器件IGBT的开关频率一般最高仅有几百赫兹^[1]。低开关频率可有效降低开关损耗、提高负载最大输出电流^[2,3]，但不可避免增加了输出电压的谐波含量，对电机产生不利的影响，如定子电流畸变、转矩脉动等。电机定子频率f较低时，可采用定子磁链轨迹逼近圆形的异步SVPWM。随着电机定子频率f的升高，同步SVPWM的开关频率f_sw线性增加。考虑最高开关频率的限制，在不同调制区段采取不同载波比P的同步算法，即分段同步SVPWM ^[4-6]。最后为充分利用母线电压而切入方波。

文献[7]对多种不同矢量序列的同步SVPWM算法谐波性能进行研究，基于伏秒平衡在线计算矢量作用时间，原理清晰且设计灵活，但很难获得最小的电流谐波畸变率。文献[8-9]针对两电平和三电平逆变器，研究了电流谐波最小PWM的开关角离线计算方法，文献[10]从矢量作用角度优化展开分析，提出了一种不依赖迭代初值的谐波电流最小同步SVPWM算法，虽可获得最优的电流谐波性能，但仅给出VVVF控制下的分析结果。针对牵引电机闭环控制下PWM算法切换冲击问题，文献[11]提出建立“自控电机”模型提取电流和磁链的基波分量，并通过修正开关角来补偿切换过程存在的动态调制误差，但没考虑切换前后PWM发生规律，工程实现较为复杂；文献[12]引入直接自控制（direct self control，DSC）的思想，提出一种适用于高速区的定子磁链轨迹跟踪控制算法。

本文借鉴文献[12]中的DSC思想，提出一种基于优化同步PWM的改进型定子磁链轨迹跟踪矢量控制。首先对PWM算法切换冲击问题进行说明，然后以最小电流谐波为目标设计优化同步PWM算法，基于此对本文提出的改进算法展开分析，最后通过Matlab/Simulink进行了计算机仿真验证。

2  PWM算法切换冲击问题

根据异步电机谐波等值电路可知，谐波电流i_h、谐波磁链y_h与谐波电压u_h满足如下关系：

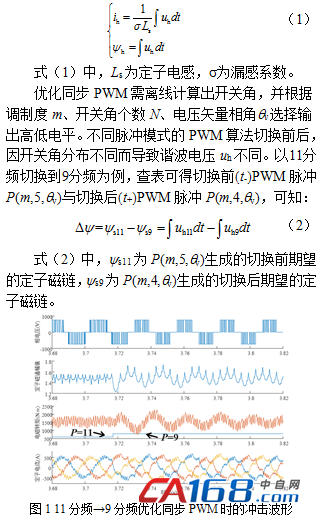
不为0的Δy是造成切换冲击的根本原因。如图1所示为本文设计的P=11，9优化同步PWM算法在无切换控制时的仿真波形，可以看到切换前后定子磁链存在明显的冲击，定子电流和电磁转矩也存在大幅度的波动，降低了系统动态响应性能。

3 优化同步PWM算法设计

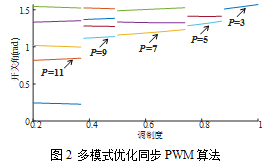
根据优化目标不同，PWM算法一般可分为特定次谐波消除、电流谐波最小、转矩谐波最小等。本文参考文献[10]的设计思路，以电机电流THD值最小为目标，得出一组多模式优化同步PWM算法，具体设计过程此处不展开，开关角曲线如图2所示。

为验证本文设计的PWM算法谐波性能的优越性，以7分频为例，分别对SHEPWM、BBCS_7和本文2种不同矢量序列PWM算法的线电压加权谐波畸变率（WTHD）^[8]进行理论计算，分析结果如图3所示，本文设计的P7-1、P7-2要明显优于SHEPWM

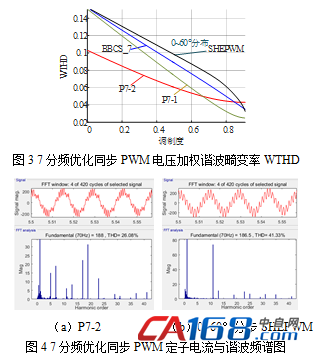
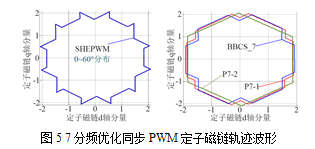
图4 7分频优化同步PWM定子电流与谐波频谱图

和传统的BBCS_7。图4所示的定子电流与谐波频谱图中，P7-2的THD值仅为26.08%，SHEPWM的THD值为41.33%，而二者的基波分量相差不大。

进一步对比图3所示4种7分频优化同步PWM的定子磁链轨迹，如图5所示，SHEPWM具有向外凸起的尖峰，P7-2为对称六边形，而BBCS_7和P7-1均为对称十八边形，不同之处在于每条边的长度。

4 改进型定子磁链轨迹跟踪矢量控制

4.1 优化开关角与定子磁链的数学关系

以P=11，9优化同步PWM为例，图6（a）为11分频A相电压波形，可以根据查开关表得到0~90°

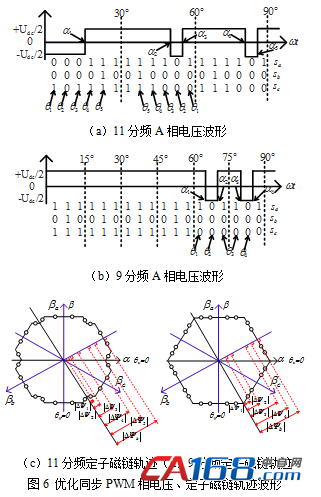
范围内的矢量序列及其相应的矢量角度q₁~q₅，同理可得图6（b）中9分频的矢量序列与矢量角度q₁~q₄。当调制度m>0.3时可忽略定子电阻的压降，根据定子电压方程可得到图6（c）、图6（d）所示定子磁链轨迹示意图，其中圆圈表示零矢量。此时11分频为对称十八边形，9分频为对称六边形。

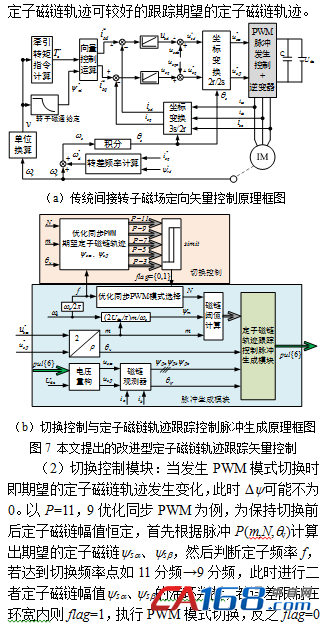
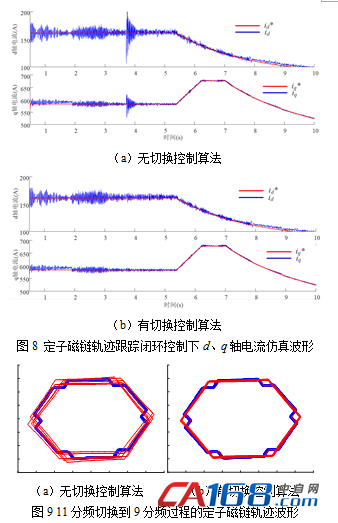
图8为定子磁链轨迹跟踪矢量控制下d、q轴电流仿真波形，可以看到无本文提出的切换控制算法时如图8（a），励磁电流分量和转矩电流分量均存在幅值不等的过冲，而加了本文的切换控制算法如图8（b），则可以完全消除11分频切换到9分频过程中的电流冲击。图9所示切换过程的定子磁链轨迹波形更直观的说明了切换控制算法的有效性，非常平滑的实现了十八边形到六边形磁链轨迹的切换。而图9（a）所示则存在一段时间的波动，从而造成图1中转矩和电流的冲击或波动。

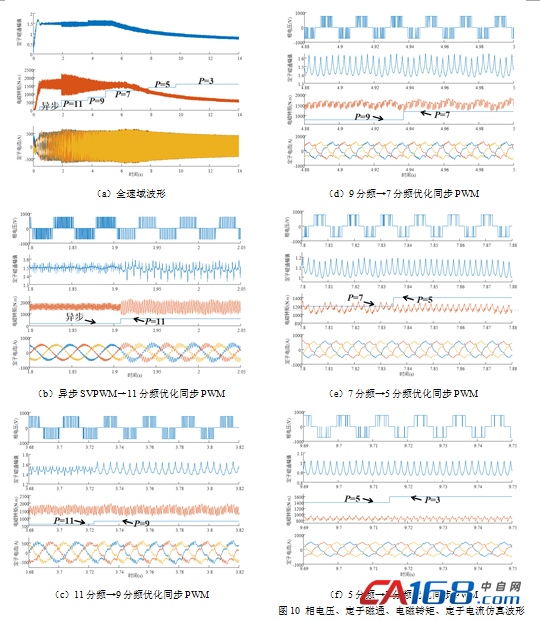
为进一步验证切换控制算法在图2所示本文设计的多模式优化同步PWM算法的有效性，图10给出了定子磁链轨迹跟踪全速域矢量控制下的相电压、定子磁通、电磁转矩、定子电流的仿真波形，随着电机定子频率的升高，脉冲模式依次为异步SVPWM→11分频→9分频→7分频→5分频→3分频，可以看到不同PWM模式间切换时，均没有出现定子磁链和电流、转矩的冲击或波动，系统动态切换性能得到了保证，验证了本文优化同步PWM算法和定子磁链轨迹跟踪矢量控制的有效性；同时对比图1和图10（c）可知，本文提出的切换控制算法效果明显。

6 结论

（1）本文设计的多模式优化同步PWM算法具有最小的电流THD值，更适用于低开关频率下的牵引逆变器。

（2）本文提出的改进型定子磁链轨迹跟踪矢量控制，可实现对优化同步PWM对应的期望定子磁链轨迹的跟踪，以保持定子磁链幅值恒定的切换控制准则可有效解决切换过程中存在的定子电流和电磁转矩的冲击或波动，提高了牵引电机运行过程中的动态响应性能，实现了异步SVPWM→11分频→9分频→7分频→5分频→3分频模式下的有效运行与平滑切换。

参考文献

[1]Bin Wu.大功率变频器及交流传动[M]. 卫三民译. 北京:机械工业出版社,2011,116-130．

[2]Abu-Rub H, Holtz J, Rodriguez J, et al, Medium voltage multilevel converters-start of the art, challenges and requirements in industrial applications[J]. IEEE Trans on Industrial Electronics, 2010, 57(8):2581-2596．

[3]Holtz J, Xin Qi. Optimal control of medium-voltage drives-an overview[J]. IEEE Trans on Industry Applications, 2013,60(12):5472-5481．

[4]Holmes D G, Thomas A L, Pulse width modulation for power converters: Principles and practice[M]. New York: Wiley-IEEE Press,2003.

[5]Patel H S, Hoft R G. Generalized techniques of harmonic elimination and voltage control in thyristor inverters：part I-harmonic elimination[J]. IEEE Trans on Industry Applications, 1973, IA-9(3): 310-317．

[6]何亚屏,文宇良,许峻峰, 等.基于多模式SVPWM算法的永磁同步牵引电机弱磁控制策略[J].电工技术学报,2012,27(3):92-99．

[7]Narayanan G, Krishnamurthy H，Zhao Di，et al．Advanced bus-clamping PWM techniques based on space vector approach[J]. IEEE Trans on Power Electronics, 2006, 21(4):974-984.

[8]马逊, 李耀华,葛琼璇,等.谐波电流最小同步优化脉宽调制策略研究[J].中国电机工程学报, 2015(05): 1211-1220.

[9]冯九一,宋文祥,姜书豪,等.三电平有源钳位逆变器同步优化PWM方法[J]. 电机与控制应用, 2015,42(11):10-15.

[10]张朝阳,张晓华,葛兴来,等.谐波电流最小优化同步SVPWM方法研究[J].西南交通大学学报, 2017,52(4)；764-773,788.

[11]Oikonomou N，Holtz J， Close-loop control of medium voltage drives operated with synchronous optimal pulsewidth modulation[J].IEEE Transactions on Industry Applications, 2008,44(1):115-123.

[12]刘可安,田红旗,尚敬,等.轨道交通异步牵引电机低开关频率下定子磁链轨迹跟踪控制研究[J].铁道学报, 2017, 39(4):1-8.

作者简介

张晓华 (1992—) 男 硕士 助理工程师 研究方向：电力牵引交流传动及其控制、功率变换器调制与控制算法