关键词：低开关频率；特定次谐波消除；开关角分布；现场可编程门阵列

Abstract: Aiming at the low switching frequency of IGBT in the traction drive system of high-power electric locomotives, this paper presents a theoretical analysis of the selected harmonics elimination (SHE) PWM algorithm and a solution to the switching angle calculation. Two sets solutions of the switching angle distribution ranges from 0~60° and 0~90° are used to compare and analyze the harmonic performance. Based on this, a method based on FPGA to realize SHEPWM pulse generation is discussed. The effectiveness of the PWM pulse generation method designed in this paper is verified by ISE/ModelSim simulation and hardware experiment.

Key words: Low switch frequency; SHEPWM; Switching angle distribution; FPGA

【中图分类号】U264 【文献标识码】B  【文章编号】1561-0330（2018）09-0000-00

 

1 引言

特定次谐波消除（selective harmonic elimination，SHE）PWM算法于20世纪70年代首次提出用于两电平电压源型逆变器[1]，输出波形质量更好的变幅变频交流电。随着电力电子技术和微处理器的发展，SHEPWM现已广泛应用在中压大功率领域，如电力机车牵引传动、级联多电平逆变器等[2-4]，其根本思想是基于单相桥臂电压波形的傅里叶级数，建立特定次谐波幅值为0的数学模型，然后求解得到一系列以调制度m、开关角个数N为自变量的开关角曲线。

本文首先对SHEPWM算法进行理论分析和开关角曲线数值求解，并对比分析了0~60°和0~90°开关角分布范围的SHEPWM谐波性能，然后探讨了一种基于FPGA实现特定次谐波消除PWM脉冲生成的方法，最后通过仿真和实验验证了所设计SHEPWM脉冲生成方法的有效性。

2 SHEPWM算法开关角求解

为简化SHEPWM的求解，通常假设三相逆变器的相电压输出波形满足半周期正负半波奇对称和1/4周期偶对称，如图1所示。则输出相电压傅里叶级数可以表示为：

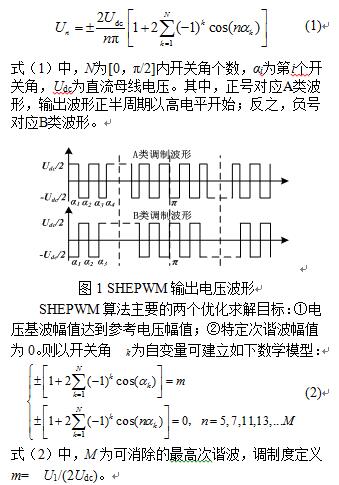
考虑三相对称性，通常对相电压的3及其倍数次谐波不作控制，仅控制6k±1(k=1,2,3…)次谐波。非线性方程组的个数与开关角个数N相等，可消除N-1个特定次电压谐波，且当N为奇数时，M=3N-2，当N为偶数时，M=3N-1。

通常采取数值计算的方法求解式(2)非线性超越方程组，并根据经验公式选择合适的迭代初始值[5]。图2分别给出了N=5时0~60°和0~90°两种开关角分布SHEPWM的开关角曲线和谐波性能对比图，可以看到不同的开关角分布对应不同的电压加权谐波畸变率，且0~90°分布的开关角畸变率更低，具有更优的谐波性能。

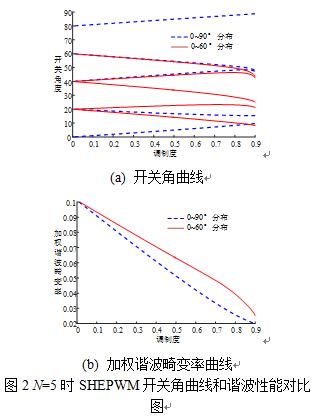
3 SHEPWM算法的FPGA实现

根据离线计算出的SHEPWM开关角，以调制度m、开关角个数N、电压矢量相角v作为输入参数，直接查表输出高低电平。PWM输出流程中存在大量的条件判断如相角区域判断，且三相互差120°独立发波，传统的数字信号处理器DSP是串行指令执行，冗长的逻辑运算会消耗掉DSP较多的指令执行时间，从而增大了整个控制周期，产生不利影响。现场可编程门阵列FPGA的高速并行特性更适合实现SHEPWM的脉冲生成。

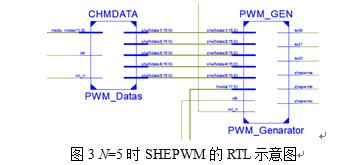
本文采用Xilinx Spartan6 xc6slx9开发板作为实现脉冲生成算法的处理器，基于ISE14.7集成开发环境和verilog HDL语言编写SHEPWM算法，并依次进行功能仿真、时序约束、软件综合、生成硬件bit流、烧写FPGA、搭建Chipscope逻辑分析仪进行硬件调试等操作。图3给出了本文编写的N=5时SHEPWM对应的RTL示意图。

4 仿真和实验验证

4.1 仿真结果

为验证本文所设计的SHEPWM算法的正确性和有效性，基于ISE14.7和ModelSim进行功能仿真分析，可得到图4所示仿真结果。可以看到，0~60°和0~90°开关角分布范围的SHEPWM三相PWM波形正确，满足对称性设计要求，不同之处在于开关角曲线不同而导致脉冲分布不同。

4.2 实验结果

在功能仿真的基础上，将本文设计的SHEPWM生成硬件bit流并下载到Spartan6 xc6slx9开发板进行单板实验，搭建硬件逻辑分析仪进行调试，图5为观测到的两种开关角分布的SHEPWM单相PWM波形，验证了FPGA实现SHEPWM脉冲生成的正确性。

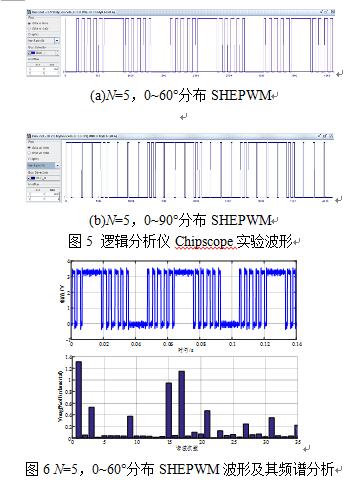
图6为示波器采集到图5(a)所示SHEPWM的波形及其FFT频谱分析结果，可以看到，除基波分量外，3次、9次、15次、17次谐波分量较大，而5次、7次、11次、13次谐波分量几乎为0，与理论分析一致，进一步验证了本文设计方法的正确性。

5 结论

本文对特定次谐波消除PWM算法的基本原理、开关角数值求解以及2种开关角分布的SHEPWM谐波性能进行了理论分析，并设计了一种基于FPGA实现PWM脉冲生成的方法，分别通过仿真和实验验证了所提方法的正确性。该设计方法同样适用于其他开关角个数的SHEPWM或优化PWM，尤其适用于高压大功率等对开关频率要求较低的工业领域，具有一定的工程应用价值。

参考文献

[1] Patel H S, Hoft R G. Generalized techniques of harmonic elimination and voltage control in thyristor inverters：part I-harmonic elimination[J]. IEEE Trans on Industry Applications, 1973, IA-9(3): 310-317．

[2] 谭新元. 牵引逆变器SHEPWM控制技术的研究[J]. 中国电机工程学报,2001, 21(9): 47-52.

[3]Holtz J, Xin Qi. Optimal control of medium-voltage drives-an overview[J]. IEEE Trans on Industry Applications, 2013,60(12):5472-5481．

[4] J. R. Wells， B. M. Nee， P. L. Chapman，et al. Selective harmonic control: a general problem formulation and selected solutions[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1337-1345.

[5] 周明磊,游小杰,王琛琛,等. 特定次谐波消除调制方式的谐波特性分析[J]. 电工技术学报,2013,28(9):11-20.

张晓华(1992—)，男 硕士 助理工程师 主要研究方向为电力牵引交流传动及其控制、功率变换器调制与控制算法