1 引言

Delta型并联机器人[1]是目前工业应用最为广泛的并联机构之一[2]．近几年来，随着工业的快速发展，并联机器人的研究及应用主要向着轻量化、快速、灵活等趋发展，尤其是在分拣、装配等重复性的流水作业中最为常见[3]，因此提高工作效率是提高生产效率的重要途径.目前，带有视觉的 Delta 并联机器人分拣系统比传统的机器人分拣更能适应复杂的作业环境，提高生产效率，改进机器人的适应能力,是目前分拣路径规划普遍采用的模式，即并联机器人主要是分拣传送带方向最前方的物料，未能充分发挥生产自动化的优势.随着智能控制技术的发展，智能控制算法逐渐应用于工业控制领域，使其系统性能更加稳定、生产效率显著，所以引进机器视觉[4]和智能控制算法的并联机器人分拣系统具有广阔的前景。

为了满足当前高速化的生产需求，提高生产效率，国内外许多学者对最优时间轨迹规划进行了深入研究， 但是从大多数文献见文[5-6]中可以看出，研究都集中在对单个分拣轨迹的优化，而在分拣系统中，Delta并联机器人的工作流程是分拣连续不断的物体，是由无数个拾取轨迹组成的。针对以上问题，对于排列密集的，无方向要求的物体实时分拣系统，本文把分拣作业按照一个抓取过程进行分组处理，以装满一个包装盒为基准，提出了一种基于改进神经网络优化算法的分拣路径优化方法，在保证每个分拣过程的轨迹进行最优化处理的同时，对处于每一个抓取过程中的所有物体进行基于神经网路的动态目标最短分拣路径的整体路径规划，并保证实时性;建立并联机器人与周围环境的紧密联系，主要是为了实时快速抓取操作，改就系统的适应能力，提高并联机器人的工作效率。

2 单个分拣轨迹的优化

2.1 研究背景

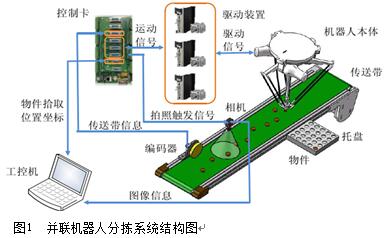
如图1所示，Delta并联机器人分拣系统主要由视觉部分、机器人抓取部分、传送部分以及控制系统组成。随机分布的物料随着传送带匀速进入到视觉采集区，工业相机以频率采集物体的图片信息，然后通过视觉系统对目标物体进行快速标定，同时利用不重复识别跟踪方法获得禽蛋的坐标信息，然后将这些信息打包传送给控制系统，对单个的目标物料进行路径规划，通过缩短单个物料分拣的时间来提高并联机器人的运行时间。

2.2 轨迹优化

分拣作业要求Delta并联机器人的快速高效运行，因此高速运动的机器人在惯性及外部受力的作用下，其连杆的变形、位移等因素不仅会影响机构的精度、降低系统运行的稳定性和可靠性，同时会影响机器人的工作效率和使用寿命。为了保证运行的平稳，必须对并联机器人的运行空间轨迹进行优化。通过分析分拣系统的运动特点，文中引用了文献中的方法，将Delta并联机器人的运动轨迹，采用圆弧连接直线规划，将机器人抓取动作分为5个动作流程，如图2所示，其中Q0-Q1、Q2-Q3和Q4-Q5采用直线插值，长度分别为L1、L2、L3，Q1-Q2、Q3-Q4采用圆弧插值，长度为L4和L5，总的长度用St表示。

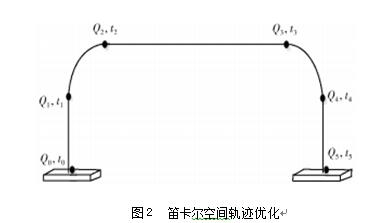
确定了使用圆弧平滑直角过渡区域后，下一步的工作就是沿着轨迹采样获得插补点的位置、速度、加速度。从缩短加减速时间、运动平稳等指标出发，必须使用专门的柔性加减速控制方法。目前常见的直线加减速、直线加抛物线加减速、指数型加减速等方法在初始和结束阶段的加速度突变不连续，都不满足高速Delta并联机器人抓取过程的平稳，七段式S曲线加速度连续，在高速数控系统中应用广泛，但加速度在切换时有突变，并且对于分阶段的确定及时间的计算较为复杂。为了减少刚性冲击，采用加减速更为柔顺、计算更为简单的修正梯形加减速算法，加速度规划如下，

3 整体分拣路径优化

3.1 问题描述

为了寻求分拣的最短路径，我们先建立相应的数学模型，可以看出此模型类似于旅行最优问题，同时，分拣路径优化具有更多的约束条件．若把传送带上的物体和托盘比做两个城市群，并联机器人比做旅行商，可以看出:物体城市群位置动态变化，旅行商在两个城市群之间交替穿行。而有很多关于TSP问题的研究采用粒子群算法、蚁群算法等，他们都是针对静止的城市群分布进行规划优化，没有分析城市群动态变化对规划的影响。为了分析方便，文中以5个城市为例对分拣流程进行说明。Delta 并联机器人起始位置为原点O，如图3所示，按照前文优化的门型轨迹进行分拣，门高为b，抓取动作顺序为O→Ai→Bj→Ai+1→Bj+1，可以看出，拾取和放置动作的行程有所不同。

拾取动作：机器人从定点Bj出发，拾取传送带上移动的物体i+1，在并联机器人运动的过程中，传送带也一直保持运动，理想的拾取是并联机器人与待拾取的物体同时到达同一个位置，因此需要通过计算预测此位置点的准确坐标。起始时，并联机器人终端执行器位于原点Bj，此时刻第i个物料处于坐标A'i，第i+1个物料处于坐标A″i+1，机器人运行时，物体随传动带向前运动，由图中可以看出，物料i+1的拾取位置是A'i+1，即并联机器人终端执行器和物料i+1同时到达该点，因此可知，此过程物料i+1运动的时间与并联机器人运行时间相等。

放置动作：执行器抓取到物料i+1后，放置到定点位置Bj+1。

以上两步完成一个分拣动作，如此往复循环完成一个分拣任务，如图3所示。

3.2 神经网络描述

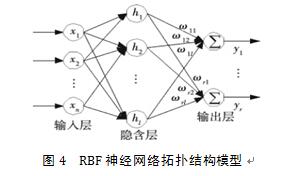
RBF神经网络是由J Moody 和C Darken 在20世纪80年代末提出的一种神经网络。RBF神经网络的基本思想是：用径向基函数作为隐单元的“基”，构成隐含层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间，使得在低维空间内的线性不可分问题在高维空间内线性可分。当RBF的中心向量和宽度确定以后，输入层到隐含层的变换也就确定了。隐含层空间到输出层空间的映射是线性的，即隐含层的输出信号，通过线性加权求值作为输出层节点的输出值，此处的权值为网络可调参数。由此可见，从总体上看，网络由输入到输出的映射是非线性的，而网络输出对权值而言又是线性的。由输入层、隐含层和输出层构成的一般径向基神经网络结构如图4所示。

                             

4 实验论证

4.1 神经网络预测

首先根据RBF神经网络的结构，我们将拾取物体的起点和终点为输入信号，并联机器人拾取的目标位置为输出，取多组拾取的样本通过神经网络模块利用输入输出样本集对其进行训练，即学习和调整网络的权值和阈值，使网络实现给定的输入输出映射关系，最终通过仿真预测目标物料的位置信息，提前规划并联机器人的运行轨迹，缩短拾取时间。

4.2 仿真实验

然后通过上面所述的拾取过程路径优化方法，并获取神经网络预测数据后，我们设置机器人的作业区间为400mm×400mm的矩形区域，取垂直高度为b=100mm；最大加速度a_max=6g，终端执行器的速度上限为v_max=5m/s，单个分拣过程的数量M=N=25，神经网络的初始种群数m=100，通过Matlab进行仿真测试后，系统阶跃响应结果如图5-图6所示。

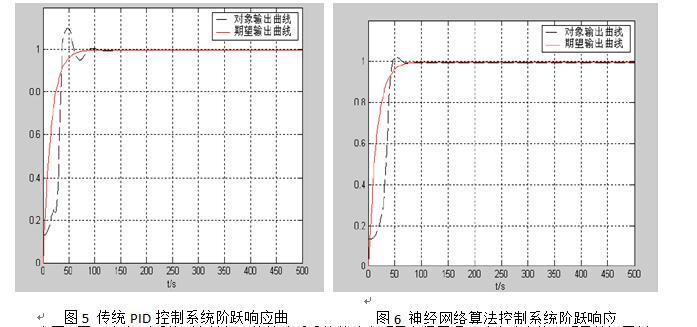
由图5-图6可知经过系统引入神经网络算法后系统的响应明显变得平滑，响应速度快，明显缩短了并联机器人的分拣时间，从而提高了工作效率。

5 结论

为了解决采用RBF神经网络进行学习训练的并联机器人位姿检测存在的收敛问题，针对Delta型并联机器提出了一种运用神经网络和迭代优化算法结合的方法，以学习RBF神经网络的参数，并最终实现对机器人的准确高效的快速运行。仿真结果表明：

（1）所选RBF神经网络具有很好的逼近能力，能较好完成Delta并联机器人拾取物料的位置预测。

（2）该算法模型清晰地描述了流水线上物料随机分布有序分拣的路径选择优化问题，计算相对简单，易于实现。引入神经网络预测环节后能够快速标定目标物料的位置，缩短并联机器人的运行时间，通过仿真实验也证明了这一结果，具有较高的准确性和稳定性，比较适合工程实际应用。

参考文献

[1]VISCHEＲ P,CLAVEL Ｒ.Kinematic calibration of the parallel Delta robot[J].Ｒobotica，1998，16 ( 2 ) : 207-218．

[2]郎需林,靳东,张承瑞,等.基于实时以太网的DELTA并联机械手控制系统设计[J].机器人,2013,35(5):576-581.LANG Xu-lin,JIN Dong,ZHANG Cheng-rui,et al.Con- trol system design of DELTA parallel manipulator based on real-time Ethernet[J].Ｒobot,2013,35(5) :576-581．

刘辛军,谢福贵，汪劲松.当前中国机构学面临的机遇[J].机械工程学报，2015，51(13).

[4] GASPAＲETTO A,ZANOTTO V.A new method for smooth trajectory planning of robot manipulators[J]. Mechanism and Machine Theory，2007，42(4):455-471．

[5] BEHZADIPOUＲ S,KHAJEPOUＲ A.Time-optimal trajec- tory planning in cable-based manipulators[J].IEEE Transactions on Ｒobotics,2006,22(3):559-563.

[6] 张策.高速包装机械手视觉控制系统研究与开发[D].天津:天津大学，2008．

Zhang C. R&D of vision control system for a high speed pack- aging robot[D]. Tianjin: Tianjin University, 2008.

[7] 张文昌．Delta高速并联机器人视觉控制技术及视觉标定技术研究[D]．天津：天津大学，2012．

Zhang W C. Control technique and kinematic calibration of Delta robot based on computer vision[D]. Tianjin: Tianjin University, 2012.

[8] 邓明星,刘冠峰,张国英.基于Delta并联机器人的传送带动态跟踪[J].机械工程与自动化,2015(1)：153-154．

Deng M X,Liu G F,Zhang G Y.Dynamic conveyor tracking for Delta robot [J].Mechanical Engineering & Automation,2015(1): 153-154.

[9] 王云飞,朗儒林,张晨瑞.高速并联机械手最优加减速控制算法研究[J].机械设计与制造,2014 (11) :85-88．

WANG Yun-fei,LANG Xu-lin,ZHANG Cheng-rui,et al.The optimal acceleration-deceleration control research of hign-speed parallel manipulator ［J］.Machinery Design ＆ Manufacture,2014(11) :85-88．

[10］冯李航,张为公,龚宗洋,等.Delta系列并联机器人研究进展与现状[J]. 机器人，2014，36(3) :375-384.FENG  Li-hang,ZHANG Wei-gong，GONG Zong-yang, et al.Developments of Delta-like parallel manipulators:a review[J].Ｒobot,2014,36(3) :375-384．

[11] HUANG S C,JIAU M K,LIN C H. A genetic-algorithm- based approach to solve carpool service problems in cloud computing[J]. IEEE Transactions on Intelligent Transportation Systems,2015,16(1) :352-364．

[12] 于莹莹,陈燕,李桃迎.改进的遗传算法求解旅行商问题[J]. 控制与决策,2014,29(8) :1483-1488．

YU Ying-ying,CHEN Yan,LI Tao-ying.Improved gene- tic algorithm for solving TSP[J]. Control and Decision,2014,29(8) :1483-1488．

作者简介：

郭振魁（1989.11-） 男 硕士 太原科技大学 研究方向：智能控制系统算法