关键词：温度；流量；PID控制；串级控制系统

1 引言

现代化过程工业向着连续化和大型化的方向发展，生产过程也随之日趋复杂，而对生产经济效益﹑质量的要求，对生产的可靠、安全性的要求以及对生态环境保护的要求也越来越高。不仅如此，生产的安全性和可靠性，生产企业的经济效益已经成为衡量当今自动控制水平的重要指标。初期的工业过程控制系统大多采用基地式的仪表和单元组合仪表，控制系统的架构也多为单输入，单输出的控制系统，过程控制理论是以频率法和根轨迹法为主体的经典控制理论，以保持被控参数温度、液位、压力、流量的稳定和消除主要扰动为控制目的过程。

串级控制、前馈控制和比值控制等复杂的工业过程控制系统逐渐应用于现代工业生产中，电动和气动单元组合仪表开始大量被使用，同时计算机和电子技术也开始应用于工业过程控制领域，实现了直接设定值控制（SPC）和数字控制（DDC）。同时新型的分布式集散控制系统（DCS）、计算机技术、通讯技术、控制技术、图形显示技术和故障诊断技术为一体，使工业自动化进入控制管理一体化的新模式。如今工业自动化己进入计算机工业集成过程系统（CIPS）时代，并依托控制理论，人工智能和运筹学相结合的智能控制技术正向工厂综合自动化方向发展。

MATLAB因其具有根强功能扩展的能力，可与其主系统一起，配备其他的工具箱，完成一些特定的任务。MATLAB具有丰富的，可用于控制系统分析和设计的函数，MATLAB的控制系统内部工具箱(Control System Toolbox)可提供对线性系统的分析、设计和建模的算法；MATLAB系统辨识工具箱（System Identification Toolbox）可对被控对象的未知对象进行辨识和建模。仿真工具箱（Simulink）提供了交互式的操作动态系统的建模、分析和仿真集成环境。它可用结构框图代替程序建立和运行模型仿真，连续、离散及混合系统；非线性、适应线性系统；单任务和多任务离散事件系统^[1]。

2 锅炉水温度模型建立

本控制系统将锅炉的水温作为主要的控制对象，将进水的流量作为辅助的控制对象。目的是在加热功率恒定下，控制锅炉水温度的恒定^[2]。如图1所示为锅炉水温度控制流程图。

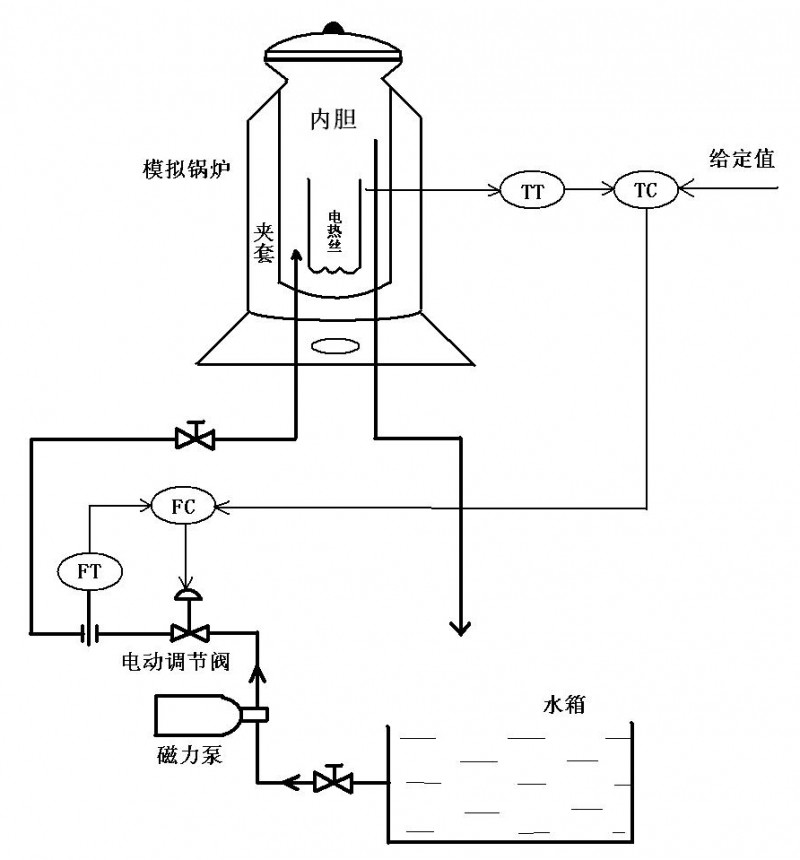
图1 锅炉水温度控制流程图

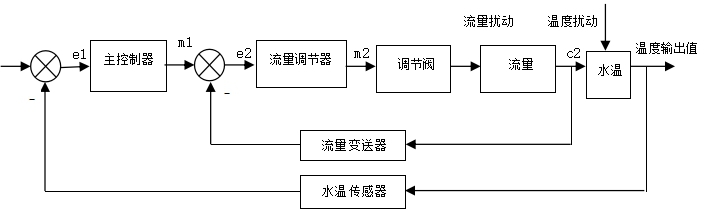
由主检测温度变送器将锅炉温度信号转变成电信号，与温度设定值进行比较后送到控制器中，控制器的流量输出控制值与副流量变送器反馈的进水流量比较后输出给副流量控制器，通过流量调节器控制给水调节阀开度来控制进水的流量，由此来完成锅炉水温的控制^[3]。其如图2所示为锅炉水温与流量串级控制系统框图。

                                              

图2 锅炉水温与流量串级控制系统框图

在控制系统设计中，对被控过程中的控制对象建立数学模型。被控对象数学模型的准确性是设计控制系统、分析质量指标、确定控制方案和整定调节器参数的重要依据。被控对象数学模型的动态特性是指在各输入量作用下，其相应被控量变化函数关系的数学表达式。

在本锅炉水温-流量串级控制系统中，在一定的电热功率下控制好水温的恒定。给水流量作为系统被控对象，需通过测定和计算出数学模型，进而来对控制系统的稳态性能和动态特性进行分析。通过仿真实验建模的方式，分别对被控对象的温度和流量在输入的阶跃信号后相关参数和响应曲线进行测定。

通过监控软件组建人机对话窗口，改变调节阀的开度,实现对被控对象输入的阶跃响应，

编写程序如下：

流量Pv=Pv1

温度Pv=Pt                          /测量值显示输出

If set=0 then

Output=6

Endif                              /set为0时输出6mA电流给调节阀

If set=1 then

Output=8

Endif                              /set为1时输出8mA电流给调节阀

其中：set可由按钮设定的外部输入信号，Output为输出电流值（mA）。电动调节阀的输入信号为4—20mA。输入6mA电流对应调节阀开度为12.5%。8mA电流则对应25%的开度。对应的流量测量值分别为6.5和10.2。阶跃值为10.2-6.5=3.7。阶越响应曲线如图3所示。

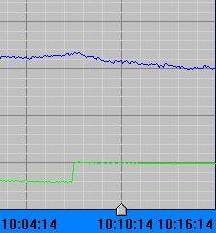
图3 试验测得阶越响应曲线

当给定阶跃信号后，锅炉温度逐渐下降至稳定，为方便处理，将数据的第一次采样值作为标准，逐渐转换为上升至稳定的曲线。转换方程为y=33.71-x。其中x为处理前数据，y为处理后数据。通过试验测得阀的给定开度分别为12.5、25、40、80时，对应的测得流量值分别为6.5、10.2、14.6、26.2。

通过MATLAB软件对实验数据进行处理，根据实验数据和最小二乘法原理对节约响应曲线进行拟合计算出水箱的模型。如图4所示，采用多项式近似拟合出水箱流量阶跃响应拟合曲线。

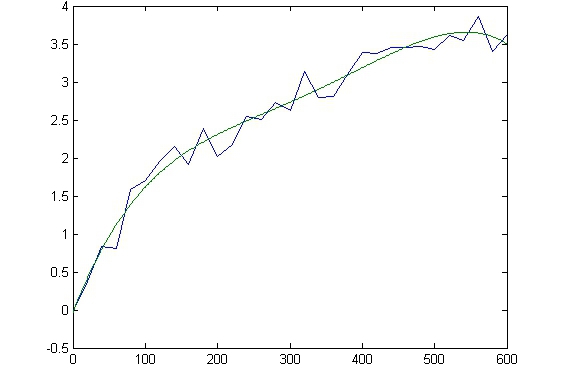
图4 水箱流量阶跃响应拟合曲线

3 控制系统框图设计

本设计考虑给水流量的变化快，时间惯性小，快速响应，采用了串级控制，将给水流量作为副被控参数，副环是随动控制，为追求控制的快速性，采用P调节，P调节器的输出信号直接控制阀的开度从而改变给水流量，水流量传感器检测信号反馈给P调节器形成负反馈，此闭环系统作为内环。温度变化也相对平缓，时间惯性较大，作为主被控的参数，主环作为定值的控制，追求控制的准确性，因此采用PID调节。得到控制系统框图如图5所示。

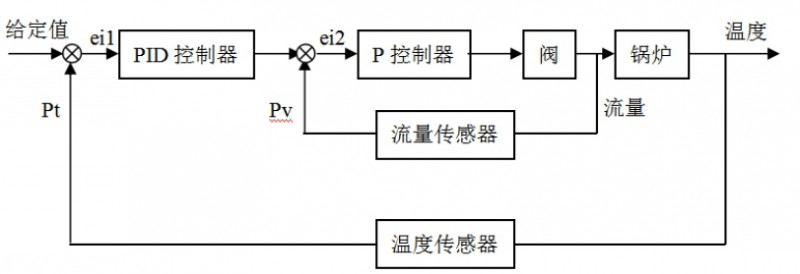
图5 控制系统框图

4 Simulink控制系统仿真

Simulink可以模拟出动态地在给定多种信号作用下构造的控制系统响应^[4]。模拟PID控制器的传递函数可分解为同一信号分别经比例P、积分I、微分D运算后相加得出；P为纯比例调节环节；锅炉的传递函数已求得；假定流量调节阀为纯比例，在实际应用中，由于阀存在动作死区，将阀的传递函数作为非线性环节处理，得到非线性系统图，如图6所示。

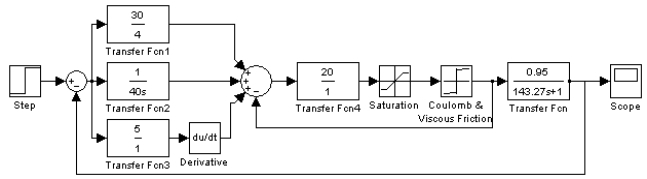
图6 Simulink控制系统非线性仿真

Saturation和Coulomb&Viscous friction两个环节相互组合形成了阀的流量特性^[5]。Saturation为限幅环节，上限幅值为100，下限幅值为0，Coulomb&Viscous friction函数设为y=0.30x+2.9。

串级控制因其具有很强的抗二次干扰能力，在串级控制系统副回路中加入一组阶越响应信号来模拟对流量的干扰，如图7所示。

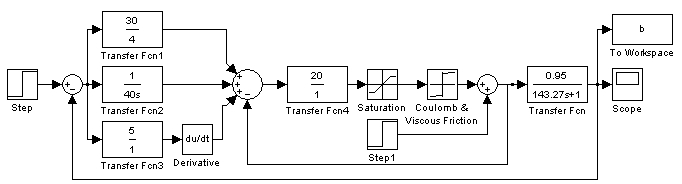
图7 串级控制抗干扰能力测试系统结构

单回路系统采用PID控制器直接对流量进行控制。在同样位置加入流量的阶跃响应干扰信号如图8所示。

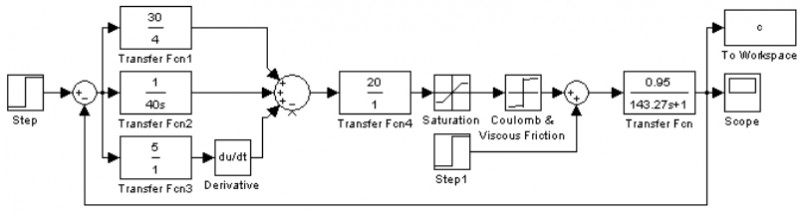
图8 单回路控制抗干扰能力测试系统结构

加入干扰信号，分别对图6和图7中的控制系统进行仿真，仿真时间均设为4000s，采样时间设为20s。干扰信号阶越时刻发生在2000s，阶越终值为18。

5 仿真结果

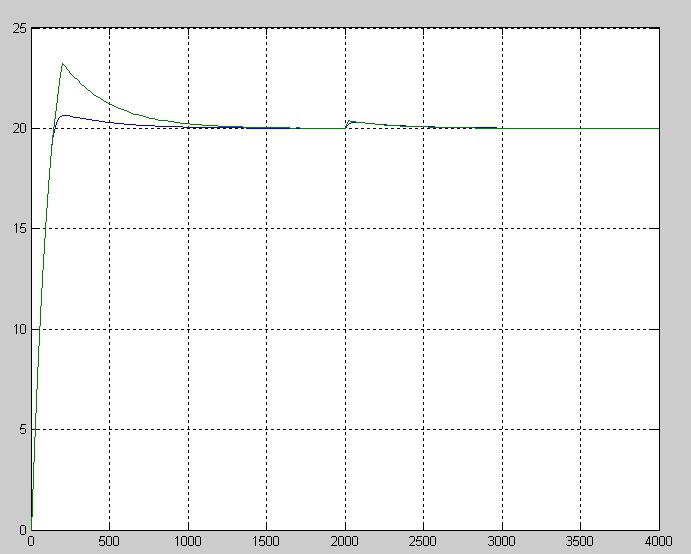
图9 控制系统抗干扰能力比较图

在图9中绿色曲线表示单回路控制系统的响应曲线，蓝色曲线为串级控制系统的响应曲线。两控制系统在上升阶段基本吻合，调节时间上基本相同，但单回路控制系统的阶跃响应超调量偏大，分析曲线并综合各种指标可认为两控制系统在阶跃信号下无干扰的控制效果基本相同。在此基础上，加入流量干扰信号，单回路控制系统在干扰信号的作用下，最大偏差达到0.42，为稳态值的2.1%左右，在曲线的末端出现了小幅度的波动。但串级控制系统在干扰信号作用下，产生的最大偏差仅有0.1左右，因此可认为此系统仍处于稳定状态。充分证明了串级控制在抑制二次干扰方面据有很强的能力。