关键词:永磁同步电机;矢量控制;电动汽车;MATLAB/Simulink软件

1引言
当今时代,全球气温变暖、生物多样性的锐减及雾霾的肆虐使得环境保护成为人们关注的大问题。燃油汽车在生态发展中的弊端变的越来越明显,而电力驱动零排放无污染的新能源电动汽车因其超低振动噪声、环保、成本低、易于维护等因素越来越受到人们的青睐,同时也成为近年来最具发展潜力的汽车市场研究方向。在电动汽车车载蓄电池没有革命性技术突破的情况下,同样作为电动汽车核心系统之一的电力驱动系统逐渐的成为各大厂商的研究目标。在对各种驱动电机的研究中,其中的永磁同步电机(Permanent magnet synchronous motor,PMSM)系统以运行效率高、转矩密度大、转矩平稳性强和转子结构简单可靠的特点在电动汽车驱动方面有着极高的应用价值,这也使其受到国内外电动汽车界的高度重视。本文在MATLAB环境下,构建了的一种永磁同步电机矢量控制系统的控制模型,对今后控制设计和实现汽车制动时能量回收提供新思路,最后对仿真结果进行分析[1]。
2 矢量控制
交流电机控制中常用的一种控制技术就是矢量变换控制,由于三相电各相都会产生磁场,且磁场不是正交的,如此分析起来就相当麻烦,矢量控制的思想是将三相电向量经过坐标变换对应到相应的两项等效且相互垂直的正交分量中去。在动态响应良好、精度要求高的场合中能使得矢量控制交流电机的调速性能媲美直流电动机[2]。
改善转矩性能是矢量控制的目的,追溯到源头就是对定子电流的控制。定子侧各物理量相互关联,关系复杂,很难进行单独控制。为了解决这一问题,所测得的电机电流必须经过PI控制器(proportional integral controller)进行数学计算,然后将其从定子的三相静态结构转化成转子d-q的动态结构(平行和垂直于转子磁场方向)。同样的,电机端的控制电压也需要经过数学计算将其由转子的d-q结构转化为定子的三相静态结构,然后再输入到PWM(Pulse Width Modulation)进行调制[3]。一旦电机电流被转化成d-q结构,控制将变得非常简单。而结构变换就需要用到Clarke和park坐标变换[4]。
2.1 Clarke变换[5]
Clarke变换是将三相静止坐标系(ABC坐标系)上的数学模型变换为两相静止坐标系(α-β坐标系)上的数学模型,变换公式如(1)所示:

式中:
2.2 Park变换
Park变换是把矢量从两相静止坐标系(α-β)坐标系变换到两相旋转坐标系(dq0坐标系)中,而Park逆变换是把矢量从两相旋转坐标系变换到两相静止坐标系中。


3 永磁同步电机数学模型
矢量控制的永磁同步电机的控制系统一般由以下几部分份组成:
(1) 整流逆变模块;
(2) 速度、电流调节器;
(3) 电流控制电压型逆变器;
(4) 坐标变化模块;
(5) 空间PWM波模块。
系统中的这些部分运行情况都将影响控制性能。
为了便于研究,简化分析过程,对永磁同步电机的数学模型先做出理想状态下的假定[6]-[7],假设如下:
(1) 永磁材料的电导率为零;
(2) 不考虑转子磁场的突极效应;
(3) 不存在涡流、没有磁滞的损耗、不计铁芯饱和;
(4) 定子三相电流产生的空间磁势及永磁转子的磁通分布呈正弦波。
三相交流永磁同步电机在两相旋转坐标系dq0下的数学模型为:
电压方程[8]:


4 控制模型搭建
在仿真模型中使用到的各个模块都能够直接通过MATLAB/SIMULINK给出相应的模型。很容易实现永磁同步电机矢量控制模型的搭建,直观便捷。
MATLAB的永磁同步电机矢量控制系统的仿真模型主要由永磁同步电机模块、三相逆变器模块、三项电压电流测量模块、a-b-c坐标转换dq0坐标模块、dq0坐标转换a-b-c坐标模块、速度调节器模块、电流调节器模块以及空间矢量PWM模块等组成。
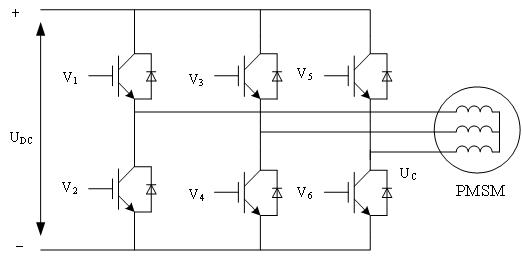
图1 三相电压逆变器电路
模型中,逆变器模块有6个IGBT功率开关器件,反向并联续流二极管,根据PWM模块给出的6组控制信号控制各个功率开关器件导通与关断顺序并于与脉宽大小的组合,从而产生三相互差120°电角度,输出相应的三相电来对永磁同步电机进行调节[9]。三相电压逆变器电路如图1所示。
根据永磁同步电机数学模型、矢量控制原理及各种逻辑关系,可在MATLAB/SIMULINK中搭建的完整的基于速度、电流双闭环的永磁同步电机(PMWM)矢量控制仿真模型。仿真模型如图2所示。
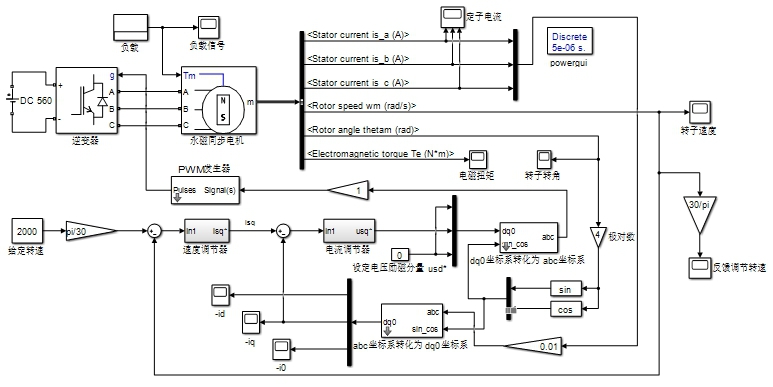
图2 永磁同步电机仿真模型
在此仿真中各项参数设置为:定子电阻Rs=0.05Ω,转子磁链为0.192Wb,电枢电感为0.000635H,转动惯量为0.011kg×m2,极对数为4,在此永磁同步电机模型上进行仿真模拟。
模型的整体工作过程为:提供560V直流电,经逆变器为永磁同步电机提供输入。在永磁同步电机输出端获取定子电流、转子转速,转子转角,电磁转矩等各项参数。后取转子转速进行速度反馈,再取三项定子电流进行坐标变换进行电流反馈,进而形成双反馈电路。后由PWM波形发生器根据反馈来的信号控制逆变器开关导,进而控制永磁电机转速。
5 PMSM仿真与分析
5.1 PID调节
依靠搭建好的Matlab/Simulink模型逐步调节系统中的相关参数来实现最优控制。
在优化后的系统中,在给定转速不变下突加负载研究两种情况下(低范围内负载和高负载)永磁同步电机的影响,并对示波器采集到的数据进行分析。
首先需要对双反馈电路中相应调节器的PID[10](比例(proportion)、积分(integral)、微分(differential))模块参数分别进行调节以获得更好的反馈效果。在速度调节器模块和电流调节器模块中都包含着PID调节子系统,因速度调节器和电流调节器内部PID系统相似,在此仅以速度调节器内部系统为叙述对象,仿真结构如图3所示。
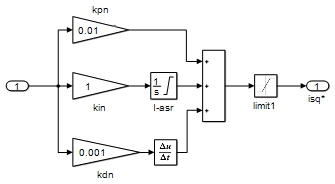
图3 调节电路中的PID模块
使用如图3所示的PID参数得到的输出转速如图4所示。
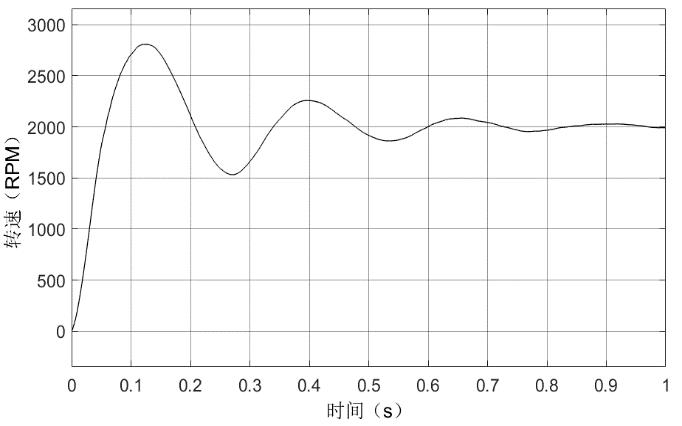
图4 初始PID数据下转速波形
从图4中能发现,在该参数下波形存在着较大的稳态误差,较高的超调以及很长的动态响应时间。对于PID参数可知,调节P值可以用来较小稳态误差;I值可以用来消除误差;D值可减小超调,克服震荡并且能够加快系统的动态响应。所以需要重新调节PID参数。
经过多次PID数据调节对比,得到相对较为稳定的PID参数。速度调节器中:Kp=1.5,Ki=1.5,Kd=0.01;电流调节器中:Kp=0.7,Ki=1.5,Kd=0。在此参数下可得到稳定的输出,如图5所示。
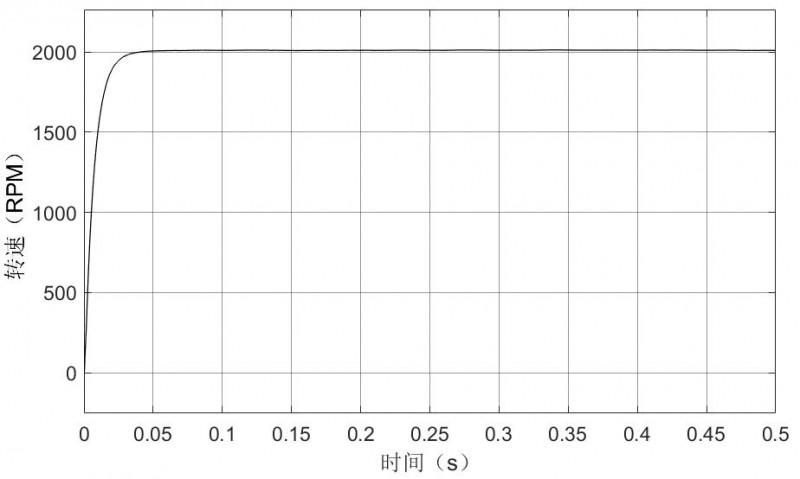
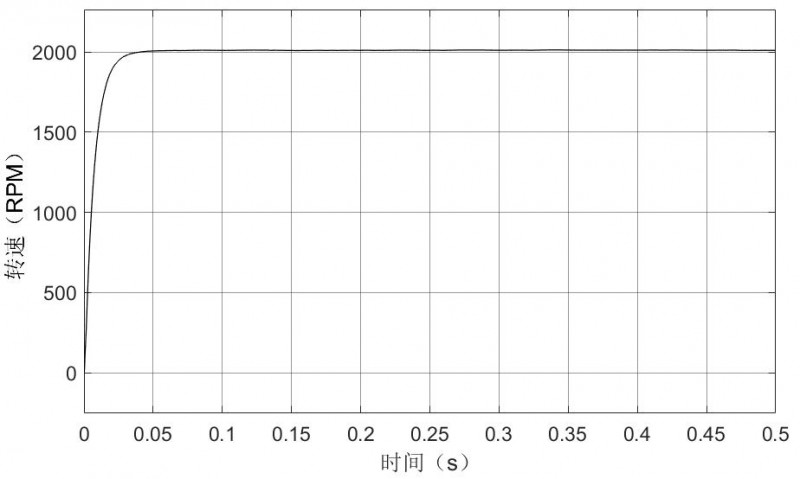
图5 优化后转速输出波形
5.2 PMSM仿真模拟结果
仿真一:在给定转速下,在t=0.2s和t=0.35秒时加入负载,负载大小分别为20N×m和60N×m。运行仿真模型的各项数据结果如图6~图8所示。
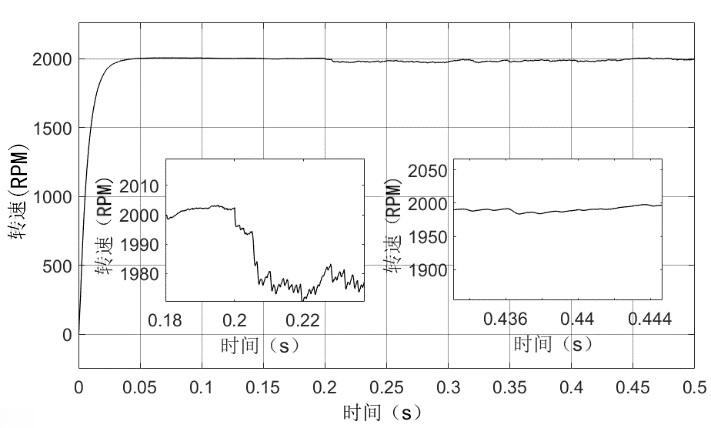
图6 可控负载下输出转速
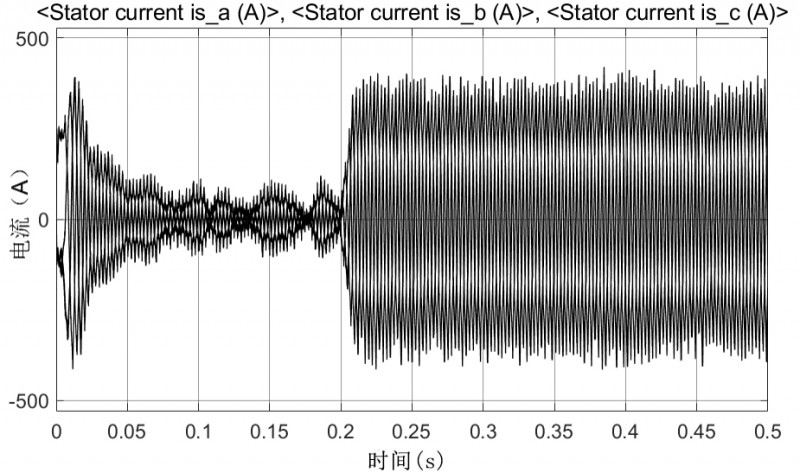
图7 可控负载下三相电流
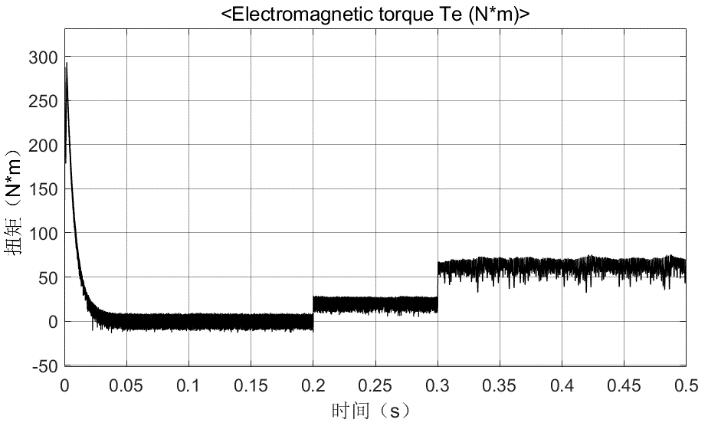
图8 可控负载下电磁转矩变化
仿真二:在给定转速下,在t=0.2s提供超出永磁同步电机可控范围负载(大小为80N×m),在t=0.3s时提供大小为10N×m的负载,再次进行仿真得到的各项结果如图9~图11所示。
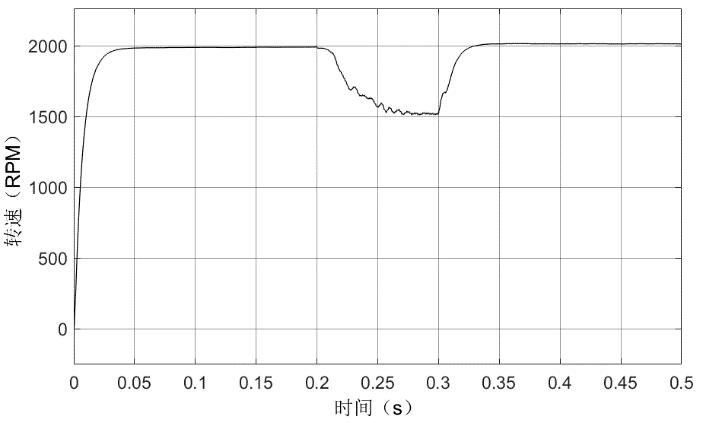
图9 高负载下转速变化
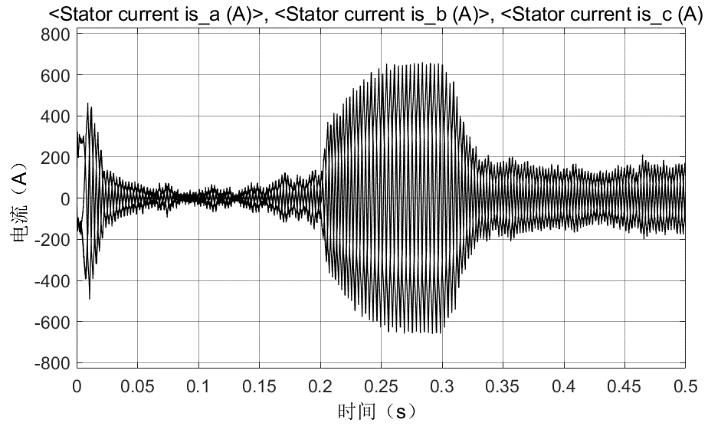
图10 高负载下三相电流
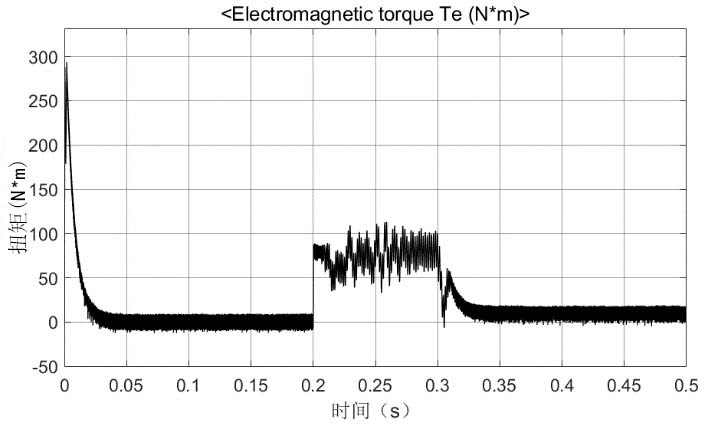
图11 高负载下转矩变化
5.3 仿真结果分析
在仿真过程中,无负载情况下,电机始终能够稳定的输出给定2000rpm转速运行(如图5所示);三相交流电电流也仅在刚开始启动的抖动后便进入稳定状态;转矩也在电机的启动瞬间迅速衰减至稳定状态。
从仿真一中的各项仿真曲线可以看出,从启动开始转速便迅速上升保持稳定,定子的三项电流也在启动的瞬间些许抖动进入稳定状态,转矩在启动时由高转矩快速进入稳定。在t=0.2s和t=0.35s时提供大小为20N×m和50N×m的负载后,能够观察到电机转速会产生小幅度的下降,但之后又逐步恢复到给定转速状态(如图6所示局部放大部分为转速跳变与恢复),同样因为有负载的加入在t=0.2s时电机电流和电磁扭矩都会产生相对原来无负载时较大的稳定输出,后又在t=0.35s时进一步的增大并处于稳定状态(如图7和图8所示)。
仿真二下,刚开始启动时装束迅速上升保持在稳定给定转速2000rpm,系统转矩也处于大转矩状态并快速下降。在t=0.2s提供大小为80N×m的负载后,转速开始出现较明显下降的变化,t=0.3s后甚至出现断崖式下降(之后仍可以处于某一稳定值),因在t=0.35s后负载改为大小10N×m,转速恢复稳定至给定转速。在这整个过程中定子三相电流会出现逐渐增大的状态,在t=0.35s后改为较小负载后进入稳定值。电磁扭矩同样存在放大的不稳定抖动,在处于可控范围内负载后进入稳定状态。
根据以上所得仿真波形综合分析可知:(1)在空载状况下,永磁电机的输出快速且稳定是一种较为理想的状态。(2)在突然加入负载时,该系统能够快速做出反应,电流、电磁扭矩均能够在瞬间提升,输出转速能够在短时间内恢复。此模型在启动、变负载情况下均具有最快的响应速度,因而适合于对响应速度有严格要求的场合。(3)在永磁同步电机承受高负载运作时,虽能够达到某一稳定,但电流、电磁扭矩存在较大波动,不建议在此中状况下启动电机。
6 结束语
通过MATLAB/Simulink软件对永磁同步电机矢量控制系统仿真分析。从对比结果可以看出:本文设计的双闭环永磁同步电机矢量控制模型能够很好的控制电机转速的稳定输出,同时也能够做出快速且稳定的回馈反应。电动汽车运行时不可不免会遇到爬坡、刹车、启动和变速的情况。电动汽车输出转矩就需要有快速的动态响应来应对频繁的变化的状况。为实现电动汽车驱动系统的最优控制,制定一个好的控制策略,电动汽车的驱动系统的有着重要的意义。
另外,随着科技的不断进步,智能化的控制系统逐步受到关注。因此可以在此研究基础之上,设计采用模糊PID的永磁同步电机矢量控制以及自适应神经网络的电机控制等控制精度更高智能网控制方式。同时也可以将此类控制推广到仿生机器人、磁悬浮、无人驾驶汽车、等极具发展前景的新兴领域中去。










共0条 [查看全部] 网友评论