与单个小车相比，多小车协同作业具有高效和稳定的工作特性。而多小车组能够相互配合完成复杂任务的一个重要前提，是各小车对于周围其他小车的相对位置的感知。基于小车之间相互的位置信息，整个小车组可以表现出更好的群蜂行为^[1]。而这种群体机器人被广泛应用于很多行业，例如机场扫雪，地震后的搜救以及农业上的播种等^[2]。近年来，业界常用的小车定位方法有GPS（全球定位系统）以及高速激光定位^[3]。而这些定位方法都具有价格昂贵的缺点，同时GPS无法在地下矿洞等信号屏蔽的地方使用，而激光定位也对使用环境有限制^[4][5]。本文采用LED光作为信号源，对LED光信号进行频率调制，可以使得小车组中的成员相互通信，同时每一个小车使用不同的载波频率从而光信号处于不同的信道。采用一种廉价的光强传感器来探测LED发出的光信号的强度幅值，达到在通信的同时感知周边小车的相对距离和相对方位的目的。廉价的传感器存在精度低，数据易漂移和对噪声有较差的鲁棒性等缺点，需要设计更为准确的估计器来弥补传感器的问题。对于线性高斯白噪声系统，KALMAN滤波器可以给出最优无偏估计，对于一般的非线性系统，可以采用EXTENDED KALMAN估计器(EKF)^[6]。但本文中使用的传感器模型为高度非线性并且有对称性，这些特征使得EKF无法应用于本文中的场景。所以，文中设计了精确度更高的粒子估计器来解决这些问题。

2  传感器观测模型的建立

    由于每个小车都需要感知周围小车的位置，同时自己的也会被周围小车所感知，这意味着每个小车上都需要装有LED光源以及光强探测器。事实上，每个小车装有6个均匀分布于小车四周的光强传感器以保证小车可以探测到来自于任意方向的光信号。而LED光源则安装在小车的中心位置。本文中使用的光强传感器的读数随着探测到的光源距离和角度的不同而变化。使用坐标来表征光源相对于传感器的距离，光源相对于传感器的方位角则用表示。小车组系统模型如图1所示。

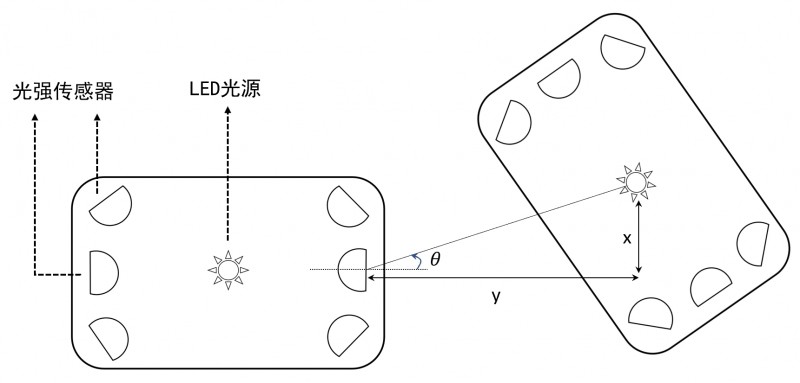
图1  小车组系统模型

    读取不同位置时传感器的读数，可以发现，随着光源距离的增加，传感器的读数减小。而随着方位角从到变化，光强的读数呈现出先增大再减小的趋势，并且传感器读数关于方位角为对称。光强读数随方位角和距离变化趋势如图2所示。

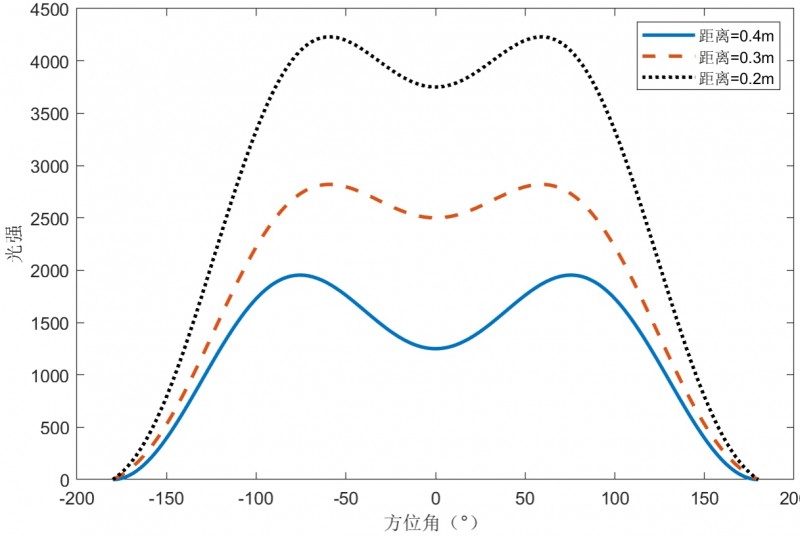
                                                                                 图2  光强读数随方位角和距离变化趋势

3  数据采集和拟合

3.1  实验数据采集

       采集的实际数据点越多，拟合出来的曲线越会接近实际值。同时，需要尽可能采集到不同角度，不同距离时的数据。设计实验如下，将小车组放入MOTION CAPTURE系统中，固定放置1号小车，而2号小车则需要以一定的半径围绕1号小车顺时针圆周运动。本文中使用的传感器有效范围为0到1.2m，所以半径从0到1.2m每间隔0.2m取一次值。小车的运动轨迹如图3所示。

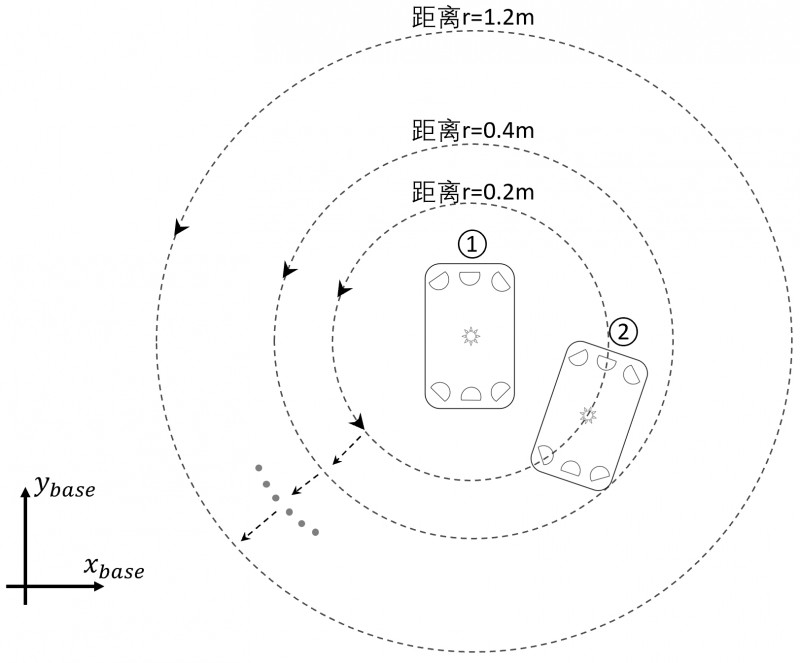
图3  数据采集实验中小车的运动轨迹

3.3  数据拟合

去掉处理后得到的数据组中的极端异常值，然后进行线性插值以提高拟合结果的准确性。处理后的数据组图如图4所示。

图4  处理得到的传感器读数与角度和距离

  （9）

4  非线性状态估计器的设计

4.1  建立小车组的空间状态模型

本文的目的是估计运动中的小车在临近车辆坐标系中的位置，而小车的运动包含直线运动与转向运动，所以小车的车头朝向角度也是系统中需要估计的状态。假定马达控制小车做匀速运动，但是由于环境的干扰，小车的速度会受到噪声的干扰并不能真正匀速行驶，那么小车的直线运动速度和转向运动速度也同时需要估计。通过基本的运动学分析，可以建立如下的离散空间状态模型：

     (10)

4.2  粒子滤波器设计

粒子滤波与EKF等高斯滤波估计方法的一个重要区别是，粒子滤波器不需要依赖确定的后验函数而使用一定数量的样本表示后验值。而粒子滤波等非参数滤波可以更好地表征一些复杂的多峰置信度^[8]。

本文中采用1000个粒子作为粒子滤波中后验分布的样本，如式（21）所示：

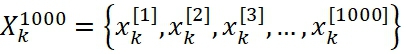         (21)

而每一个粒子代表着小车在时间点时可能的状态。

4.2.1  初值的选取

4.2.6  粒子缺乏问题

多次重采样之后，有可能会出现某次重采样到的粒子中并没有包含状态真值的情况。而重采样并不是一个可逆的过程，这样会导致多次循环后，估计值会收敛为一个错误值，即粒子缺乏问题。本文中，为了解决这一算法的局限性，在每次重采样之后，舍弃误差值较大的25%的粒子而掺入同样数量的随机粒子。

4.3  状态估计结果

估计器对小车状态的估计结果如图5中所示，可以看到几次迭代后，估计值迅速向实际值收敛，坐标值的估计误差在以内。粒子集可以很好地追踪小车的运动轨迹，实验结果符合预期。
                                       

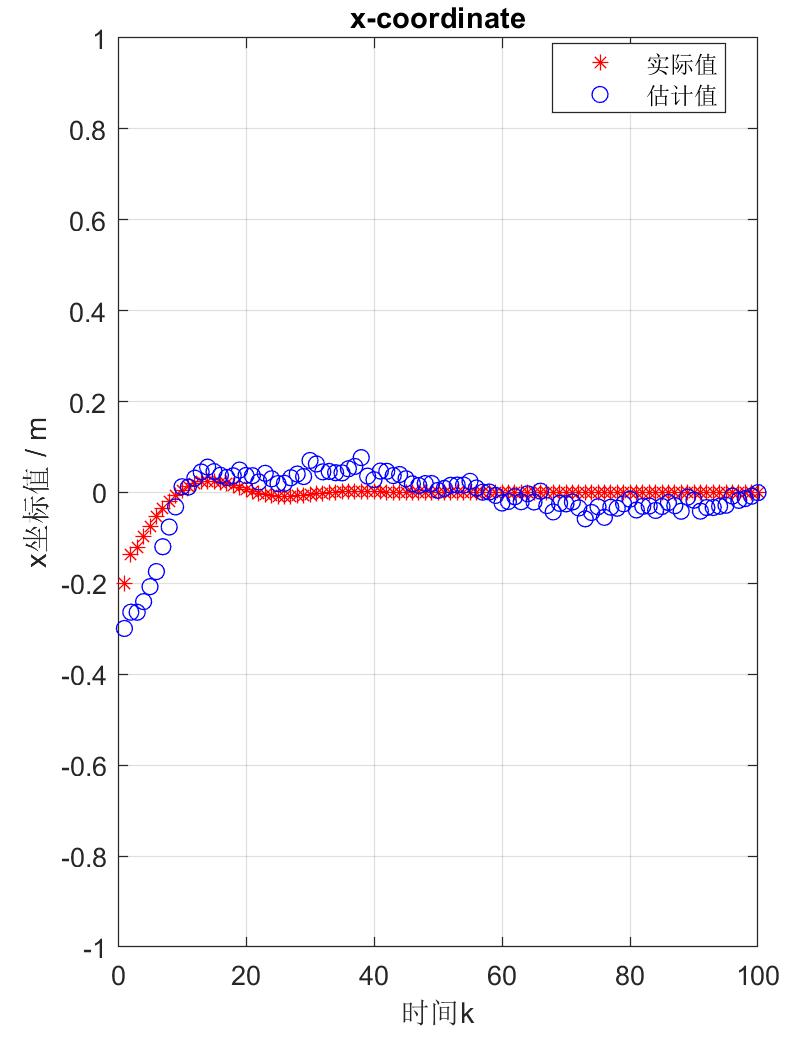
图5（a）  x坐标估计结果

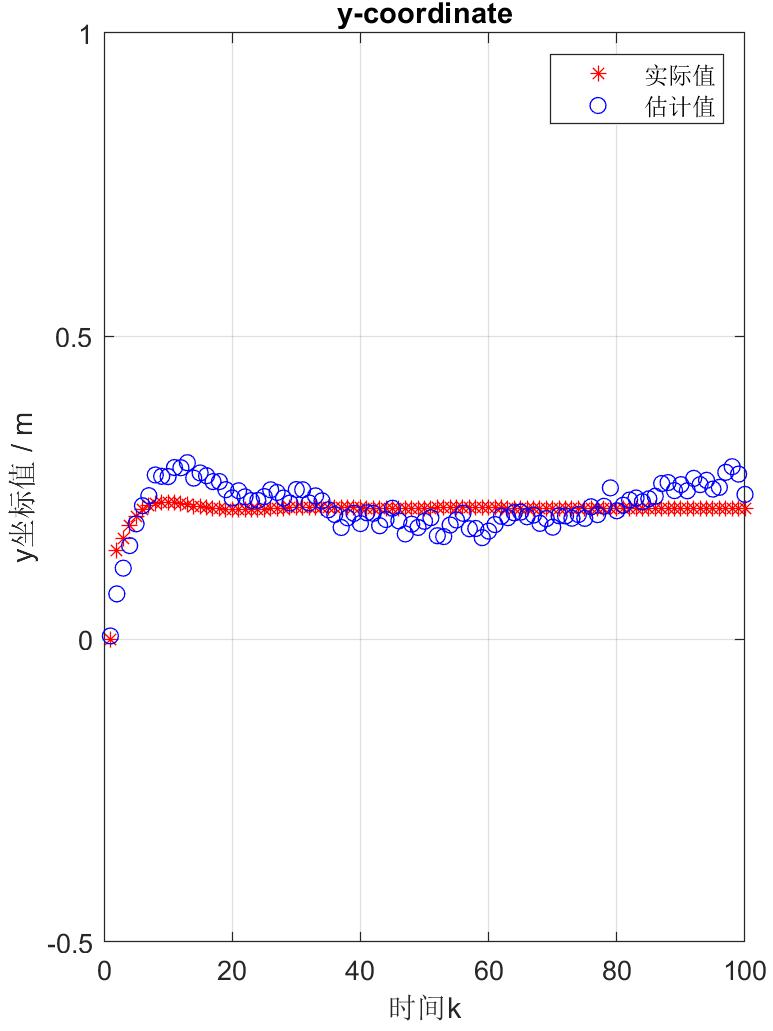
图5（b）  y坐标估计结果

5  结论

（1）本文使用了价格低廉的光强传感器配合准确的粒子滤波估计器完成了多小车组中各个成员的相互定位。对光信号采取频率调制的方式使得小车组中每个小车都具有唯一的信道，从而减少多小车定位时的相互干扰。

（2）采用先建立含参数学模型，然后采集实验数据拟合的方式获得高度非线性的传感器函数模型。

（3）粒子滤波器的设计过程中，使用重采样的方法解决了粒子退化的问题。同时在重采样后加入一定数量的随机粒子，避免了多次重采样可能导致的粒子缺乏现象。