关键词：直接转矩控制；开关磁阻电机；滞环控制器；转矩脉动抑制

1  引言

    开关磁阻电机调速系统（简称SRD）是一种新型调速驱动执行系统，它主要由开关磁阻电动机本体、位置检测结构、电流检测结构、控制单元和功率变换器五个部分组成。相比较于传统异步电机，开关磁阻电机结构简单，转子上无绕组，只有定子上有集中式绕组，所以相比于传统异步电机，开关磁阻电机运行速度快、制造成本低^[1-3]。目前开关磁阻电机已经应用于牵引运输、电动车辆、航空工业、家用电器和伺服控制等领域，显示出了其强大的竞争力。由于开关磁阻电机是一个非线性系统，传统控制方法下的开关磁阻电机运行时会产生较大的转矩脉动。

    直接转矩控制（Direct Torque Control , DTC）方法来源于传统异步电机中的直接转矩控制，DTC的控制思想是同时对电机的转矩和磁链进行反馈控制，通过对于转矩和磁链的调节选择合适的电压矢量提供给功率电路，达到直接控制转矩的目的。

2  SRM直接转矩控制系统的设计

2.1  SRM的转矩特性

SRM的运行原理为：磁通总是遵循着最小磁阻而导通，导通后产生磁链扭曲产生转矩，产生机械能^[4]。如果忽略磁场饱和或者磁场之间的相互影响，那么转矩仅与电流和转子的位置有关。电磁转矩的方程可以表示为：

2.2  DTC控制原理

DTC系统框图如图1所示，DTC控制策略对转矩和磁链进行闭环控制，根据转矩和磁链的偏差选择电压矢量，然后控制功率电路使电机工作在期望状态^[5]。不同于SRM的传统控制方法（开关角控制、电流斩波控制和电压斩波控制）在直接转矩控制中不需要控制开关角或者预设电流滞环。

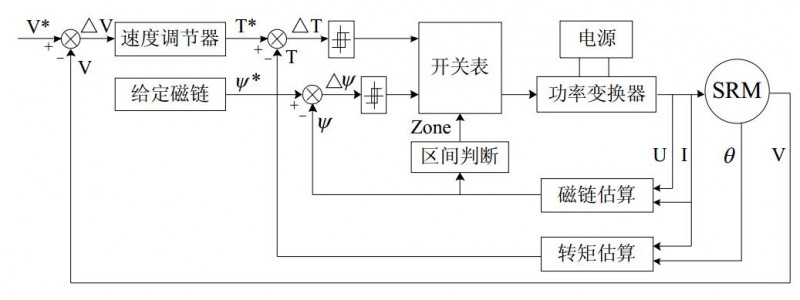
图1 开关磁阻电机DTC系统框图

2.3  电压空间矢量的选择

    本次仿真选取功率变换电路采用了半桥式结构。电压空间矢量与电机的相数和各相电压的状态有关，对于本次研究所选择的6/4极对数的三相SRM，有三种电压状态，如图2所示^[6]。拿出单相绕组的电压状态为例，“1”状态下，开关管T1、T2导通，此时绕组中被施加正向正向电压，电路处于激励状态。“0”状态下，T1关断T2导通，此时电流下降速度缓慢，磁链变化较小，电路处于续流状态。“-1”状态下，T1、T2均被关断，此时二极管D1、D2导通，电路被施加反压，磁链迅速减小。因此，对于三相电机共有3³=27个空间电压矢量可以选择，选取6个对称的空间电压矢量（0，1，-1），（0，-1，1），（1，0，-1），（-1，0，1），（-1，1，0），（1，-1，0）如图3所示，作为直接转矩控制的电压空间矢量。选取的空间电压矢量将平面分为了6个扇区，每个扇区的边界为相邻空间电压矢量的角平分线，可以得出以下结论。当磁链位于Ⅰ扇区时，以逆时针方向为正方向，电压矢量V2、V6可以使磁链增大，V3、V5使磁链减小，V2、V3可以使转矩增大，V5、V6可以使转矩减小。

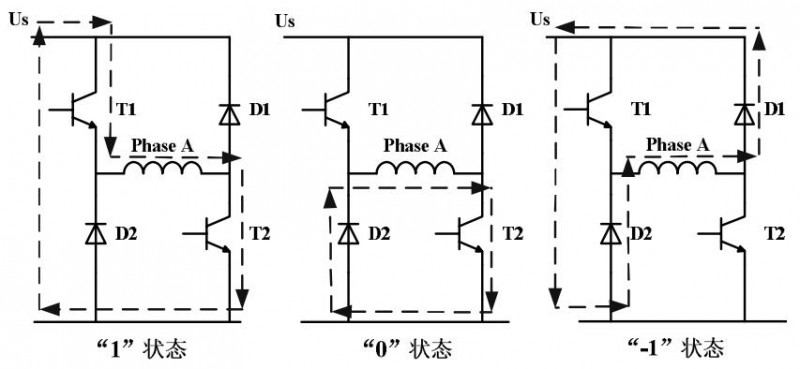
                                                        图2  SRM单相绕组的电压状态

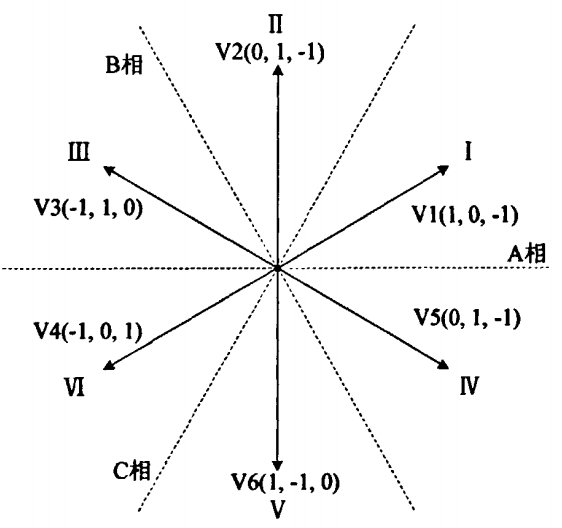
                                                           图3 选取电压矢量示意图

将6个扇区中的电压矢量、磁链和转矩的关系分析完成之后，可以将其列为控制矢量表，在附表中Τ↑、Τ↓分别代表转矩上升和下降，Ψ↑、Ψ↓分别代表磁链上升和下降。

                  附表  电压空间矢量表

转矩和磁链的反馈是直接转矩控制所必须的，转矩大小可以通过电流和转子角度信息通过查表法得到，由于本次使用SIMULINK进行仿真，可以直接从SRM的本体模型中引入转矩反馈。根据电压方程可以推导出磁链的表达式：2.4  磁链检测与扇区判断

（2）

通过式（2），当采集到绕组的电压和电流后，可以计算出定子磁链值。为了方便进行就算，将磁链从三相坐标系转化为两相坐标系如式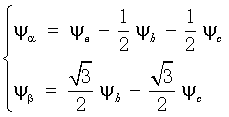（3）：

    （3）

变换后的磁链大小和角度由式（4）计算：

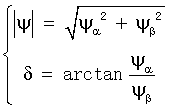           （4）

扇区的选择可以依据的值决定，当的值在[0°，60°)之间时，磁链位于扇区Ⅰ，之后每隔60°增加一个扇区，扇区Ⅵ对应值区间为[300°，360°)。

3  DTC系统仿真模型的设计

    本文将SRM的DTC调速系统在MATLAB中建立仿真模型，主要包含了开关表选择模块，模糊PI模块，磁链扇区判断模块，功率变换器模块，磁链计算模块，开关磁阻电机本体模块等。本仿真系统框图如图4所示，其中模糊PI模块仿真如图5所示。本次仿真的步长是10^-6s，求解算法是ode45。

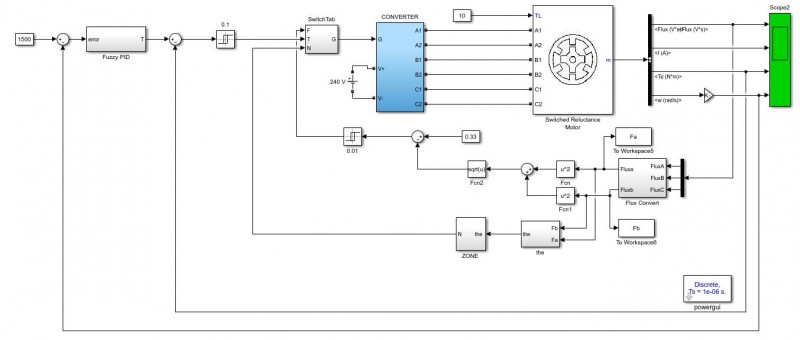
图4 基于模糊PI的直接转矩控制仿真图

图5 模糊PI模块仿真图

本次仿真中，速度外环反馈值先与参考转速相比较，然后经过模糊PI输出参考转矩。输出的参考转矩与实际转矩相比较，构成转矩内环。

4  仿真结果与分析

    本次仿真的参数如下：转速1500r/min,负载转矩为10，转矩控制器滞环限幅为0.1。在如图5所示的模糊PI控制器中K_p=25，K_i=20，模糊控制器采用三角形隶属函数，模糊因子和解模糊因子由公式计算得到。
     本次仿真将产生的磁链幅值传输到MATLAB的工作空间，在MATLAB的命令窗口下使用plot函数绘制出磁链轨迹图，将使用模糊PI的直接转矩控制的磁链轨迹图与使用电流斩波控制（Current Chopping Control，CCC）产生的磁链轨迹图相比较，如图6所示。从图6中可以看出，电流斩波控制(CCC)的磁链轨迹呈现三角形运动，结合模糊PI的直接转矩控制磁链为一个近似于圆形的椭圆，可以看出磁链反馈及其滞环把磁链控制在幅值合适的范围之内，磁链轨迹稳定。

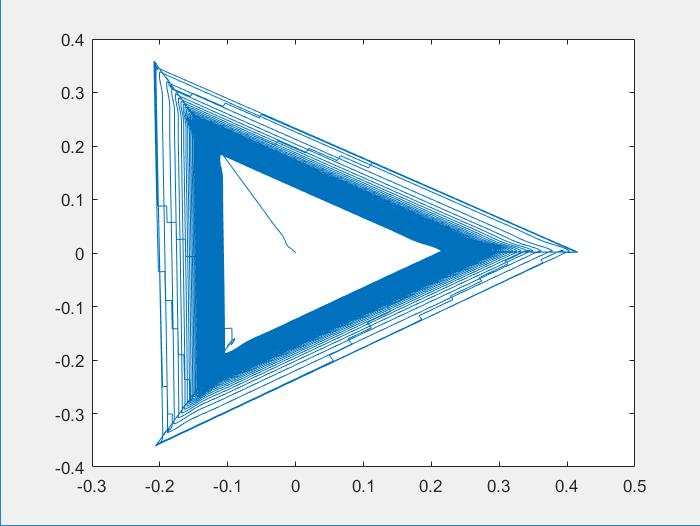
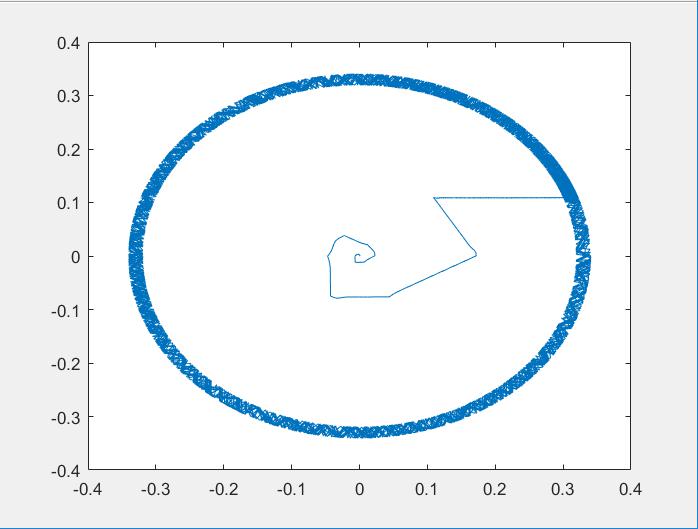
                                                                      图6 磁链轨迹比较图

                                                

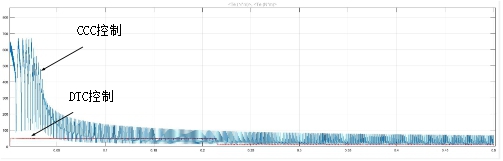
                                                                图7  转矩波形比较图
     两种控制方法的波形比较图如图8所示，从图8中可以看出采用CCC控制方法的SRM转速上升速度过快，造成启动电流过大。采用DTC控制方法下的SRM，由于事先整定了PI参数，并且通过模糊算法对PI参数进行在线调节，转速上升过程平稳，启动电流小于CCC模式下的启动电流。

                                                              图8  转速波形比较图

从图9给出了两种控制方法下的磁链波形，对比图（a）、（b）可以看出，采用模糊PI的直接转矩控制下的磁链稳定在0.4Wb左右，磁链波形基本稳定；采用CCC控制方法下的磁链发生畸变，当SRM进入稳速运行时，磁链为0.2Wb，是最大磁链幅值的33%，磁链幅值变化幅度较大。

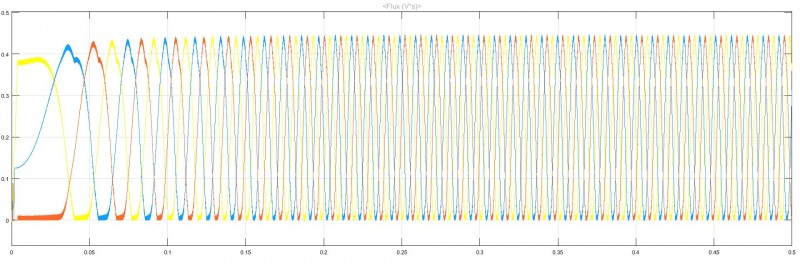
                                                （a）DTC控制下磁链波形

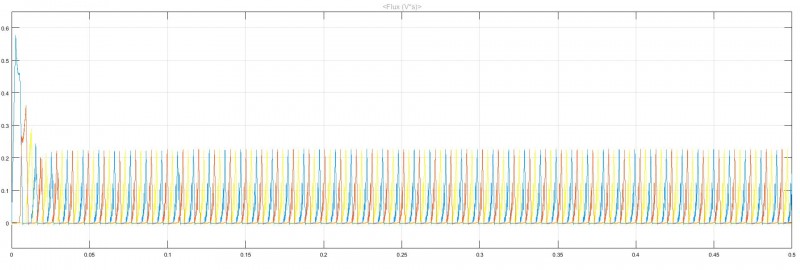
                                                                     （b）CCC控制下磁链波形

                                                             图9 磁链波形比较

两种方法下的电流波形如图10所示，在传统的CCC控制方法下，启动电流很大，被滞环限制在了200A，SRM稳定运行时电流为25A，为启动电流的12.5%，电流变化较大。而采用基于模糊PI的直接转矩控制下的SRM系统启动电流减小约为150A，当电机稳速运行时，电流为180A，电流波形稳定，对于功率电路的选型要求降低，可以有效地减小转矩脉动及噪音。

                                                      （a）DTC控制下电流波形

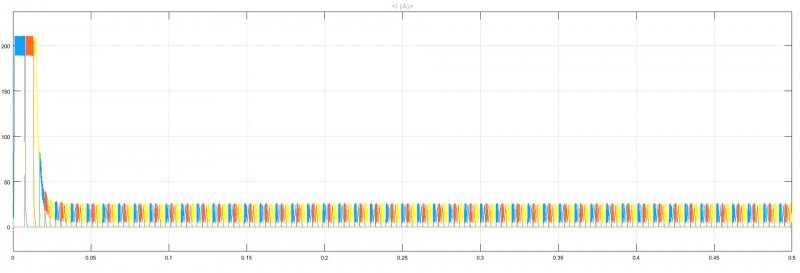
                                                         （b）CCC控制下电流波形

                                                           图10  电流波形比较

    由以上仿真结果表明，基于DTC的SRM调速系统具有以下优点：SRM的定子电流、磁链波形平滑对称，且定子磁链空间轨迹为圆形；对转矩脉动的抑制作用显著；由于能够对电机的输出转矩进行直接有效的控制，故系统动态性能优越。

5  结束语
    本文将模糊PI控制和直接转矩控制相结合应用到对于SRM的控制当中，通过MATLAB仿真结果证明基于模糊PI的直接转矩控制可以有效的对SRM的磁链幅值和转矩进行控制，有效的降低了电机的转矩脉动，提升了系统的动态性能和稳定性。