关键词:开关磁阻电机;直接瞬时转矩控制;BP神经网络;抑制转矩脉动
Abstract: Switched Reluctance Motor (SRM) has a simple structure and flexible control. However, due to the particularity of the driving method and the double salient pole structure, there are torque ripple and noise in the SRM. For the characteristics of SRM internal nonlinear factors and strong coupling, based on the direct instantaneous torque control (DITC) strategy, the outer loop introduces a fuzzy PID controller to adjust the speed, and the inner loop introduces a BP-PID controller based on BP neural network and adjust the torque online. The simulation by Matlab/Simulink shows that the improved DITC strategy can effectively suppress the torque ripple and improve the control performance.
Keywords: Switched reluctance motor(SRM); Direct instantaneous torque control(DITC); BP neural network; Suppress torque ripple
1 引言
开关磁阻电机(Switched Reluctance Motor, SRM)结构简单、控制灵活,启动电流小、转矩出力大,在各个工业领域有着广泛的应用前景。但是SRM自身的双凸极结构和驱动方式的特点导致运行时存在着转矩脉动和噪声[1-3]。为了减少SRM的转矩脉动和噪声,国内外研究者设计了多种控制方法并取得了大量的成果。文献[4]介绍了一种滑模变结构控制器在SRM中的应用,并进行了仿真设计,文献[5]介绍了一种基于模糊PID控制器的SRM调速系统,可以在线调节PID参数,并进行了实验验证。文献[6]采用局部逼近神经网络-径向基函数(RBF)网络,建立了 SRM 磁特性模型,并使用DSP控制器实现。
传统的直接瞬时转矩控制(DITC)是对直接转矩控制(DTC)的改进,该方法直接将转矩作为控制量,在换相时不需要设计转矩分配函数,易于在控制系统中的编程实现。将DITC策略与智能控制策略相结合,在速度外环上采用模糊PID控制方法对速度进行调节,转矩内环采用BP-PID对转矩进行在线调节,并使用转矩滞环控制对转矩进行限幅,实现SRM的转速和转矩变化相一致。
2 SRM的直接瞬时转矩控制系统
2.1 直接瞬时转矩控制系统设计
整个系统框图如图1所示,本系统主要由BP-PID在线调节器、模糊PID控制器、功率变换器、转矩滞环控制器模块、转矩计算模块和SRM构成。在SRM的速度外环上采用了模糊PID控制器对SRM的速度进行调节从而得出参考转矩T*,然后与瞬时转矩T进行比较,得出转矩偏差。转矩偏差经过BP-PID控制器在线调节后经过转矩滞环控制器的判断生成三相开关信号输入给功率变换器,由功率变换器驱动SRM运行。不同于传统的电流斩波控制(CCC)和角度位置控制(APC),该控制方法不需要进行位置角的设置或者设计电流闭环。
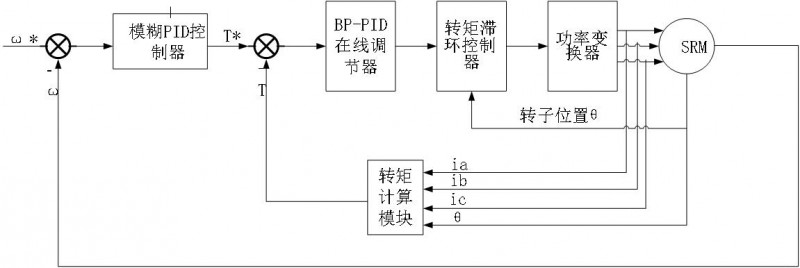
图1 开关磁阻电机DITC系统框图
2.2 模糊PI控制器的设计
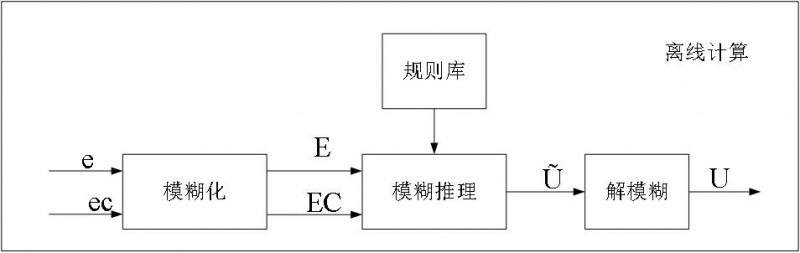
图2 模糊PI控制器设计框图
如图2所示,首先测得速度偏差e和速度偏差变化率ec,通过模糊化处理得到E和EC。经过模糊规则推理出比例因子Kp、积分因子Ki的变化范围。通过解模糊得出具体的Kp、Ki的变化量U。通过模糊PI控制算法,从而实现速度在线根据E和EC的变化来调节Kp、Ki,从而对传统的PI控制起到了在线修正的作用。
本文中模糊输入量是转速偏差e和对e求微分得到的转速偏差变化率ec,输出量为Kp和Ki。其中模糊子集分为{负大,负中,负小,零,正小,正中,正大}七个级别,分别表示为{NB,NM,NS,Z,PS,PM,PB}其论域范围为[-6,6]。
隶属函数种类很多有高斯隶属函数、三角形隶属函数、正态隶属函数和梯形隶属函数等。本文对不同的输出要求选择不同的隶属函数,其中三角形隶属函数结构简单,设计简便,输出响应快,故本文首要采用三角隶属函数,对于负大和正大的模糊化采用高斯函数,如图3所示。
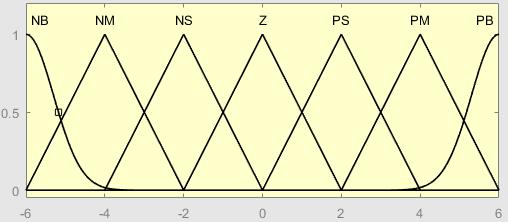
图3 Matlab中输入/输出隶属函数图
本次设计中比例因子Kp的模糊规则表如表1所示,在模糊控制中模糊规则库中存放着全部的模糊控制规则,基于专家经验或者工程方面的知识,即通过人类专家的经验将其进行一定的描述,最后形成模糊控制规则。
表1 Kp的模糊控制决策表
|
EC E |
NB |
NM |
NS |
Z |
PS |
PM |
PB |
|
NB |
PB |
PB |
PM |
PM |
PS |
Z |
Z |
|
NM |
PB |
PB |
PM |
PS |
PS |
Z |
NS |
|
NS |
PM |
PM |
PM |
PS |
Z |
NS |
NS |
|
Z |
PM |
PM |
PS |
Z |
NS |
NM |
NM |
|
PS |
PS |
PS |
Z |
NS |
NS |
NM |
NM |
|
PM |
PS |
Z |
NS |
NM |
NM |
NM |
NB |
|
PB |
Z |
Z |
NM |
NM |
NM |
NB |
NB |

2.3 转矩滞环控制器的设计
SRM的直接瞬时转矩控制中转矩滞环控制器是其设计核心,通过转矩的反馈得到实际转矩的偏差量,把这个偏差量控制在合理的阈值范围以内。为了调节输出转矩,在控制系统中是通过导通或者关断对应相的功率变换器实现的。如图4所示,拿出单相绕组的电压状态为例,“1”状态下,开关管T1、T2导通,此时绕组中被施加正向正向电压,电路处于激励状态。“0”状态下,T1关断T2导通,此时电流下降速度缓慢,转矩变化较小,电路处于续流状态。“-1”状态下,T1、T2均被关断,此时二极管D1、D2导通,电路被施加反压,转矩迅速减小。
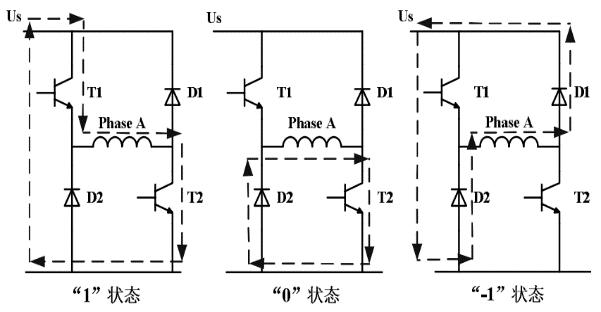
图4 SRM单相绕组的电压状态
转矩滞环控制器的原理如图5所示,T*为给定参考转矩,ε和-ε为滞环控制器设立的过门限阈值和门限阈值,S为开关状态,ΔT为参考转矩与瞬时转矩的转矩偏差。当ΔT>ε时,实际转矩小于参考转矩,此时S=1,转矩增大;当ΔT<ε时,实际转矩大于参考转矩,此时S=0,转矩减小;当ΔT<-ε,转矩过大,此时S=-1,转矩减小。
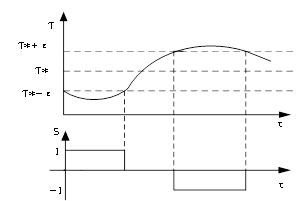
图5 转矩滞环控制器的工作原理
在SRM单相导通工作区域,单相导通滞环控制器如图6所示。当SRM的瞬时输出转矩过大会导致给定参考转矩与瞬时转矩的转矩偏差值小于滞环下限阈值ΔTmin,此时应使该相功率变换器的开关状态切换为“0”,进入零电压续流状态,使输出转矩下降;当参考转矩与瞬时转矩二者的差值大大于滞环上限ΔTmin,需将功率变换器的开关状态切换为“1”,实现当前相处于励磁状态使输出转矩不断上升。当SRM正常运行时,上述过程反复工作,使转矩偏差限定在设置的上下限阈值内,保证输出的瞬时转矩能快速响应参考转矩。

图6 单相导通滞环控制器
2.4 BP-PID控制器的设计
BP神经网络又称误差反向传播网络,BP神经网络可以包含多个输入和输出,并且在输入和输出之间可以建立一层或多个隐含层。BP神经网络结构如图7所示,从图中可以看出,这是一个三层神经网络,信号首先通过输入层输入传递系统的状态,输出层输出的三个参数Kp、Ki、Kd对系统进行控制,通过参考转矩与实际转矩的误差对于Kp、Ki、Kd进行在线调整,得到新的数值。

图7 BP神经网络结构图
设BP神经网络的输入为式(4):

BP-PID控制结构如图8所示,从图中可以看出,BP-PID控制器由两个部分构成,首先其主体结构为传统的PID控制器,其控制参数Kp、Ki、Kd由在线整定得到;其次为BP神经网络控制器,通过分析瞬时转矩误差信号e(k),和PID输出信号u(k)对BP网络中的权值进行调整,从而在线调整Kp、Ki、Kd三个控制参数,实现PID参数的最优化调节。
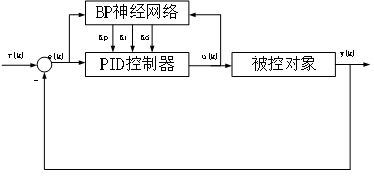
图8 BP-PID系统结构图
本次设计采用增量式PID算法,其增量式算法为式(7):
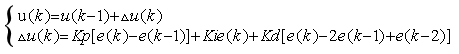 (7)
(7)
3 系统仿真模型的设计
本文将基于神经网络的SRM系统在Simulink中建立仿真模型,如图9所示,系统包括:模糊PI控制器、BP-PID控制器、转矩滞环控制器、功率电路模块、速度反馈模块和SRM模型构成。其中BP-PID控制器设计如图10所示,模糊PI控制器设计如图11所示。本次仿真的步长是10-6s,仿真时间0.5s,求解算法是ode3。
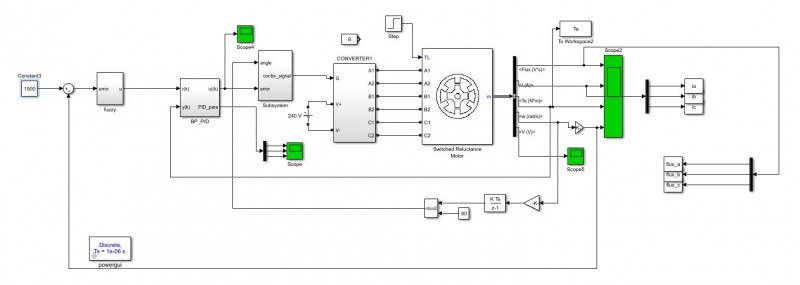
图9 SRM的系统仿真模型
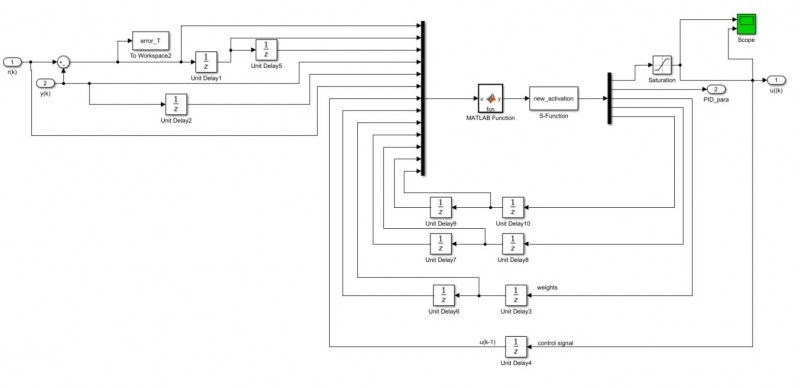
图10 BP-PID控制器仿真模型

图11 模糊PI控制器仿真模型
4 仿真结果与分析
本次设计的参数选择为:转速1500r/min,在0.2s时施加负载转矩为50![]() ,转矩控制器滞环限为0.3,外滞环限为0.5,BP神经网络采用4-6-3(输入层-隐藏层-输出层)的网络结构,如图12所示。模糊运算和神经网络运算在Matlab中完成。仿真结果如图12所示,同时与传统电流斩波控制(Chopped Current Control,CCC)的波形进行比较,进而对比出基于神经网络的DITC控制对于转矩脉动的抑制效果。
,转矩控制器滞环限为0.3,外滞环限为0.5,BP神经网络采用4-6-3(输入层-隐藏层-输出层)的网络结构,如图12所示。模糊运算和神经网络运算在Matlab中完成。仿真结果如图12所示,同时与传统电流斩波控制(Chopped Current Control,CCC)的波形进行比较,进而对比出基于神经网络的DITC控制对于转矩脉动的抑制效果。

图12 神经网络程序图
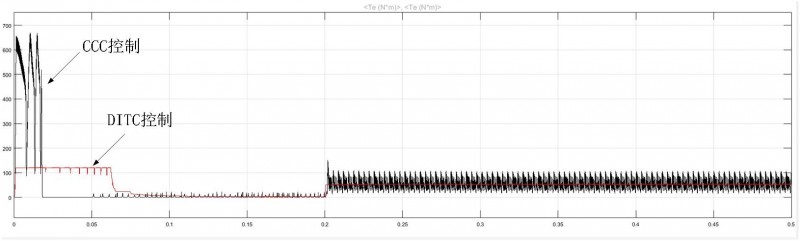
图13 转矩波形对比图

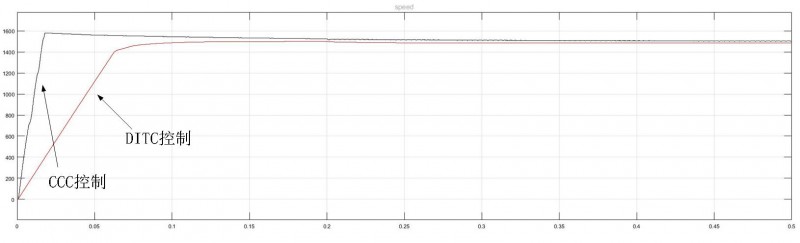
图14 转速波形对比图
两种控制方法的转速波形比较图如图14所示,从图中可以看出,CCC控制方法下的速度环上仅使用了PID控制器控制,速度上升较快,超调量为5.3%,在实际的使用过程中快速上升的速度会造成电机的振动与噪声,同时还会造成较大的启动电流。在基于神经网络的DITC的控制策略中,速度环上采用了模糊PI控制器进行控制,无超调、无震荡,电机平稳启动。
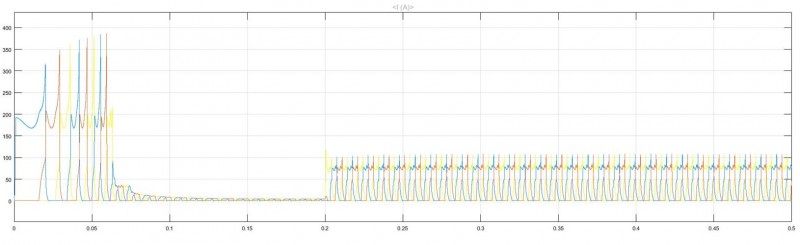
图15 DITC控制下电流波形图
在基于神经网络的DITC控制下的电流波形图如图15所示,启动电流最高为387A,电机运行平稳后电流在10A以下,在0.2s后电机带入50![]() 负载,电机带载后电流尖峰在105A左右,电流变化稳定,对于功率电路中的开关管选型要求小。
负载,电机带载后电流尖峰在105A左右,电流变化稳定,对于功率电路中的开关管选型要求小。
由仿真结果表明,基于神经网络的DITC控制具有如下优点:(1)通过转矩滞环控制器和BP-PID控制器的结合使用,有效的抑制了SRM的转矩脉动;(2)在电机启动时转速平稳,无超调、无震荡;(3)SRM运行时电流稳定,有利于功率电路器件的选择。
5 结束语
本文从传统的DITC控制策略出发,引用了BP-PID控制器和模糊PI控制器,分别对电机的转矩内环和速度外环进行了调节,对SRM的转矩和速度进行控制,有效的降低了SRM的转矩脉动,提高了系统的动态性能和稳定性。
参考文献:
[1]吴建华. 开关磁阻电机设计与应用[M].北京: 机械工业出版社,2000: 55-61.
[2]张炳力,朱可,赵韩,等.基于CAN 总线的燃料电池客车通信网络设计[J].仪器仪表学报,2006,27( s1) :657-658.
[3]宋雪桦,吴和生,刘锦娟等.混合动力汽车电池管理系统设计[J].电子测量与仪器学报,2011,25( 9) :787-792.
[4]李爱华. 滑模变结构控制在开关磁阻电机调速系统中的应用[D].南京:南京航空航天大学自动化学院,2005.
[5]苗骞,张承慧,崔纳新. 开关磁阻电机模糊PID控制系统研究[J]. 电气传动,2005,35(7):27-30.
[6]蒯松岩,吴涛,代尚方,张旭隆. 基于RBF的无位置开关磁阻电机控制系统[J]. 电力电子技术,2011,45(7):52-54.
作者简介:
蔡健(1994.6-),男,齐鲁工业大学研究生在读,研究方向:先进控制系统与应用。





共0条 [查看全部] 网友评论