关键词：电压源逆变器，死区影响，基波电压相移，永磁同步电机转子定位

Abstract: The dead time should be arranged when the power switches in the same bridge arm of voltage source inverter (VSI) are being switched. During the dead time, the load is out of control, which will cause the abnormal amplitude and phase of output voltage. Aiming at the three-phase VSI-resistance inductance series load system, the simulation analysis of the output fundamental voltage phase shift caused by dead time under various conditions is given, and the fundamental voltage phase compensation method of three-phase VSI-permanent magnet synchronous motor (PMSM) drive system is proposed, and a power circuit of three-phase VSI-PMSM drive system with phase compensation function and constant duty cycle is given. The above-mentioned phase compensation method provides a reference for improving the positioning accuracy of PMSM rotor.

Key words: voltage source inverter, effect of dead time, fundamental voltage phase shift, PMSM rotor positioning

1  引言

功率开关的物理结构和开关特性决定了其通断过程需要时间。功率MOSFET为场控器件，静态时几乎不需要门极电流，只靠多子导电，不存在少子储存效应，关断过程非常迅速。功率MOSFET开关速度依赖于输入电容的充放电速度，而输入电容取值无法降低，关断时间在10—100ns之间。IGBT由功率MOSFET和GTR（即BJT）复合而成，具有少子存储效应，因而关断时间较长，而开通时间较短。对于SiC MOSFET，死区时间可以低至800ns，对于Si IGBT的死区时间一般在1.8ms~3.5ms，依赖于IGBT的容量大小和快速性。

    对于具有桥臂结构、电压源供电的电力电子变换器，如电压源整流器（VSR）和电压源逆变器（VSI），其安全换流条件为：（1）任意桥臂不能直通，防止直流电压源短接；（2）线路电流不能断续，防止形成浪涌电压。鉴于VSI采用逆导型功率开关，续流二极管起到反向限压和续流作用，因而自然满足第二个条件。

死区设置意味着，开关状态切换（即换相）过程逆变器—负载系统处于失控状态，有利的方面是三相桥臂换流时刻并不相同，结果逆变器输出相/线电压、负载相电压的基波分量偏离理论值，影响供电质量和传动系统的调速性能。这些影响包括基波电压幅相改变，且衍生出一些新的高次谐波电压，直接影响传动系统的调速性能，对PMSM转子定位产生固定相移。

针对这些影响分析，现有文献[1-14]基本上是针对死区时间对基波电压幅值影响，没有考虑死区时间对基波电压相位影响。在参考文献[15-17]中，根据负载电流极性，采用等效方法得到方波电压，进而分析死区时间对基波电压的影响。目前大多数针对SPWM或SVPWM算法的死区补偿策略，是针对如何补偿死区对基波电压幅值影响。

由于死区对基波电压相位的影响与以下参数密切相关：死区长度、开关频率、期望输出频率、负载阻抗性质与负载轻重等，而对于逆变器-PMSM传动系统，负载轻重与调制度、输出频率密切相关。死区对基波电压相位的影响尚未得到重视，是由于影响较小，且通过闭环控制系统可以近似补偿。但是对于PMSM传动系统，尤其是对位置控制非常敏感的应用，如高性能高精度航空航天、机器人、精密数控机床、位置伺服驱动系统，由于死区比较明显地影响转子定位，因而该问题需要得到重视和解决。

对于基本脉宽调制算法，死区设置方式包括：（1）开通延时（on-delay），不具有基波电压损失的补偿能力；（2）关断提前（off-delay），同样不具有基波电压损失的补偿能力；（3）根据输出电流极性的双沿收缩（on/off-delay），具有基波电压损失的自动补偿能力。

本文主要针对上述三种死区设置方式、在a-b-c、a-b和d-q三种坐标系下对死区影响基波电压相位情况进行仿真分析，寻找其变化规律，并在d-q坐标系下给出死区影响基波电压相位的补偿策略，并提出一种调制度恒定的逆变器-PMSM传动系统的功率电路。这些工作旨在探索死区影响基波电压相位的补偿方法。

2  VSI-PMSM传动系统波形分析

2.1  典型输出电压类型

三相电压源逆变器-PMSM传动系统如图1(a)所示，将反电动势折算到定子侧后，图1(a)可以简化为图1(b)，在忽略反电动势后，图1(b)可以简化为图1(c)。图中，D1~D6构成三相二极管整流电路，S1~S6构成三相IGBT电压源逆变电路。输入三相380V正弦交流电压，输入滤波电感为200mH，直流滤波电容为两组4×680mF串联，负载为电阻5W与电感50mH串联。

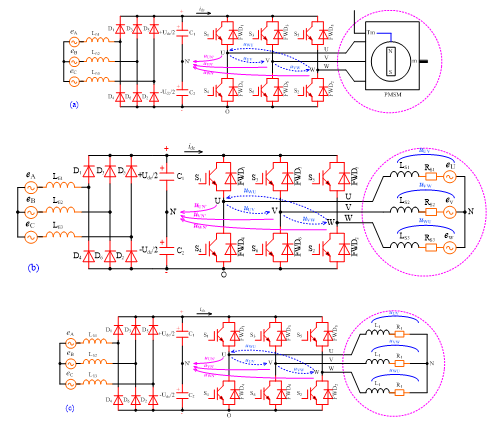
图1三相电压源逆变器-PMSM传动系统

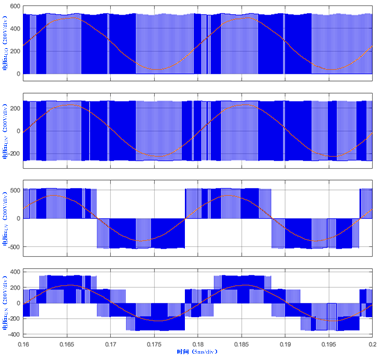
图2  三相VSI SPWM算法时各种输出电压波形

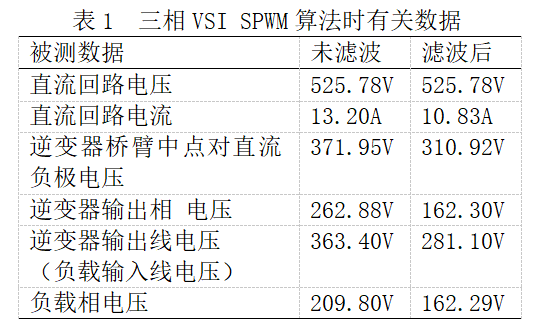
逆变器输出相电压为两电平，逆变器输出线电压为三电平，负载相电压为五电平。负载得到的线基波电压有效值为逆变器输出相电压基波有效值的2/√3倍，负载得到的相电压基波有效值等于逆变器输出相电压基波有效值。

2.3  鞍形波PWM时波形

三相VSI鞍形波PWM（Saddle PWM）算法的目标函数为

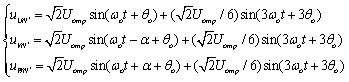 (2)

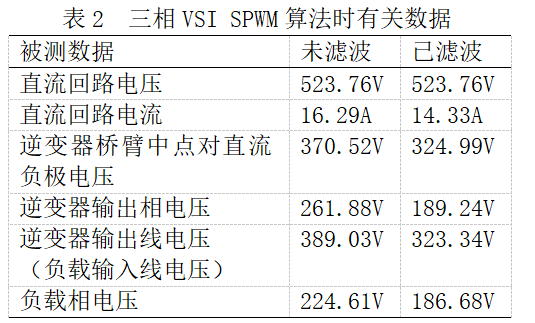
以第一桥臂U相和/或V相输出为例，双极性调制、调制度和开关频率时，四种电压及其基波电压波形如图3所示，有关测量数据如表2所示。

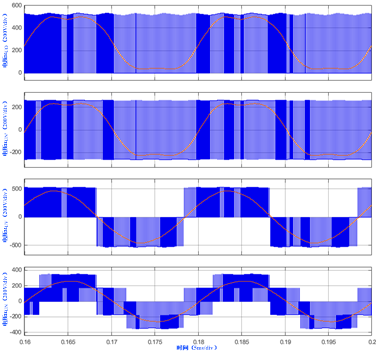
图3 三相VSI Saddle PWM算法时各种电压波形

负载得到的线电压基波有效值为逆变器输出相电压基波有效值的2倍，负载得到的相电压基波有效值为逆变器输出相电压基波有效值的2/√3。

2.4  空间矢量调制算法时典型波形

三相VSI SVPWM算法的等效目标函数有两种形成方法：

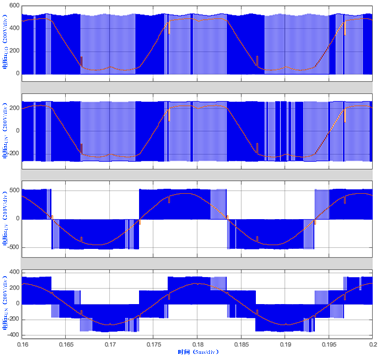
图4 三相VSI SVPWM 算法时各种电压波形

负载得到的线电压基波有效值为逆变器输出相电压基波有效值的2倍，负载得到的相电压基波有效值为逆变器输出相电压基波有效值的2/√3。

3  VSI-PMSM传动系统死区分析

3.1  死区设置方法

    不论采用传统或改进型SPWM和SVPWM算法，电压源逆变器都必须采用死区设置的安全换流方式。

    鉴于IGBT关断时，首先是门极MOSFET关断，导通电流迅速下降，然后为PNP GTR关断。由于GTR存在少子存储效应，关断出现较长的拖尾时间，因而同一桥臂功率开关切换时需要躲过IGBT关断时间t_off，包括关断延时时间t_d(off)和关断拖尾时间t_r。IGBT开通时间t_on包括开通延时时间t_d(on)和电流上升时间t_r。

    IGBT关断时间一般远大于IGBT开通时间，600V、壳温100°C时60A的Field Stop IGBT FGH60N60SFD的开通时间与关断时间如表3所示。同一桥臂上下功率开关状态切换时间称为死区时间t_d，显然t_d应该大于关断时间。

表3  Field Stop IGBT FGH60N60SFD的开关特性

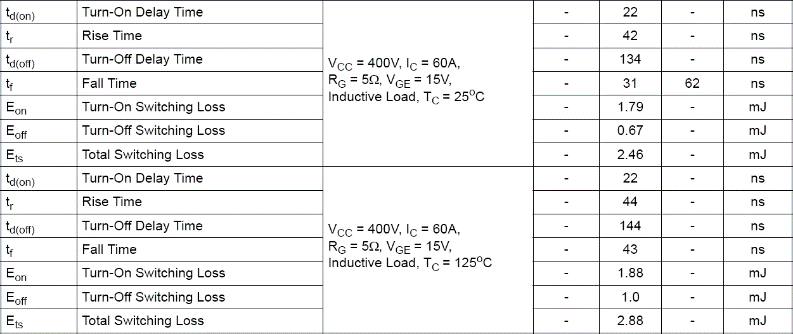
    开通延时（on-delay）的死区设置方式如图5（a）所示，关断提前（off-delay）的死区设置方式如图5（b）所示，根据输出电流极性的双沿收缩（on/off-delay）的死区设置方式如图5（c）所示，死区时间需要大于功率开关的关断时间，包括关断延时时间和拖尾时间。

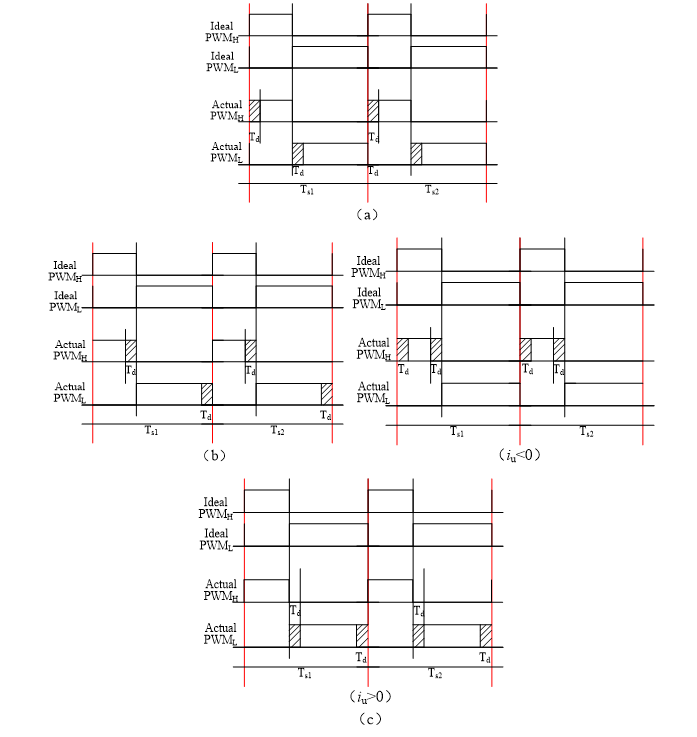
图5 电压源逆变器的三种死区设置方式

3.2  死区影响分析

VSI死区至少在以下几个方面产生负面影响：输出基波电压有效值和相位、高次谐波电压、共模电压分布等，致使输出电流发生畸变，电动机产生转矩脉动和过热，降低调速精度。逆变器输出电流失真的几个因素：（1）产生脉动失真，且与开关频率有关，开关频率高时，脉动失真较小；（2）产生交越失真，且与死区时间和输出频率有关，开关频率高时，脉动失真较小。

 对于开通延时（on-delay）的死区设置方式，图6给出了VSI理想与实际驱动脉冲、输出相电压与输出相电流对应关系，图7给出了VSI输出相电压理想波形、实际波形及其差，图8给出了VSI输出线电压理想波形、实际波形及其差，图9给出了负载相电压理想波形、实际波形及其差，图10给出了VSI输出相电流理想波形、实际波形与逆变器输出相电压偏差对应关系。

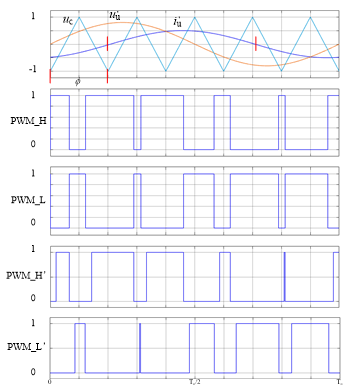
图6 VSI理想与实际驱动脉冲、输出相电压与输出相电流波形

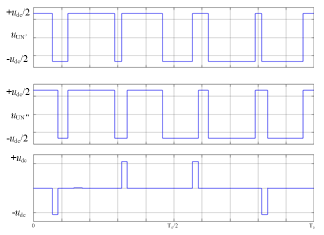
图7 VSI输出相电压理想波形、实际波形及其差

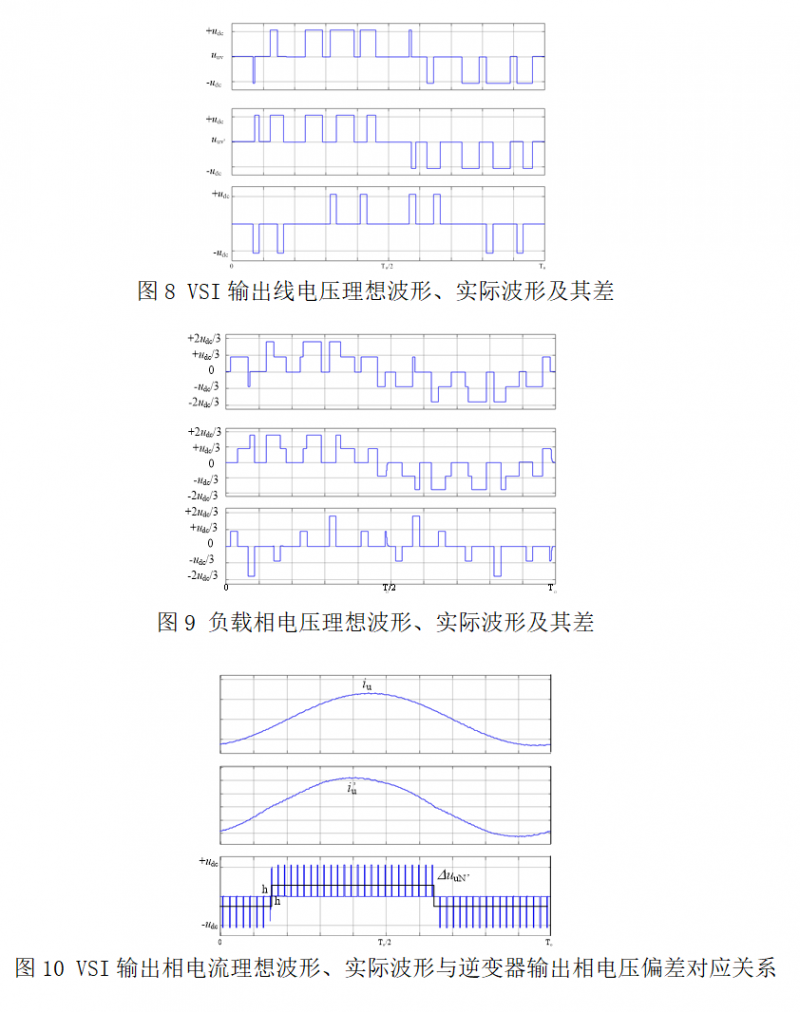
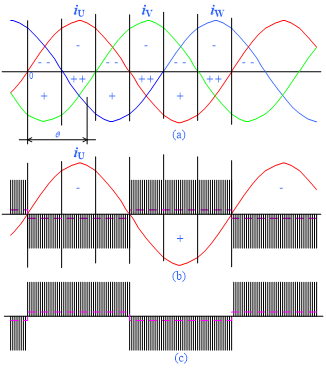
图11 输出电流极性不同时死区补偿原理

    在SVPWM算法中，死区时间引起误差电压脉冲分布如图12所示，死区补偿方法如表4所示。

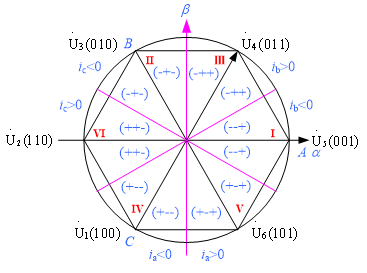
图12 SVPWM算法输出电流极性与死区误差电压关系

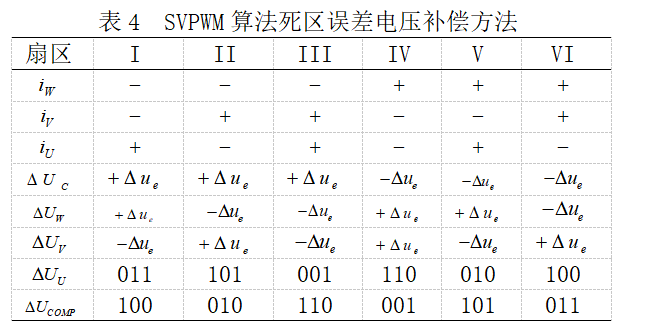
需要说明的是，扇区需要重新分配，新的开关状态采取c-b-a的顺序。表4中，DUs为误差电压矢量，其方向与6个固定矢量的方向相同；DUcomp为补偿电压矢量，其方向与DUs方向相反，但是长度与DUs相同；DUa、DUb与DUc为输出电压矢量。

3.4  有死区时相位定性分析

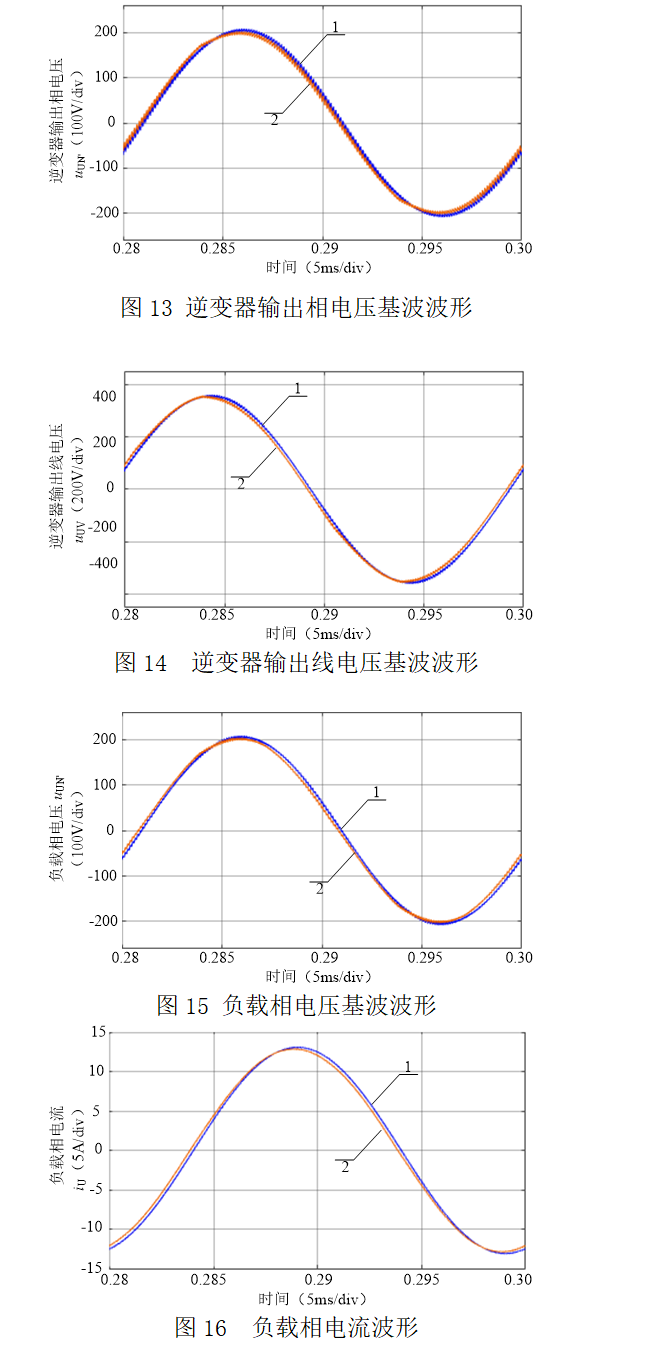
    对于3相VSI-阻感串联负载，电阻5W，电感50mH，采用SPWM算法，开关频率为8kHz，自然采样，死区时间为2ms，仿真步长为1e-7s，调制度为0.8，直流电压为538.79V，在有、无死区情况下，逆变器输出相基波电压如图13所示，逆变器输出线电压基波如图14所示，负载相电压基波如图15所示，输出电流波形如图16所示。以上各图中，曲线1指无死区情况，曲线2指有死区情况。可见，死区存在引起以上各基波电压相位均超前，且超前角相同。

 在a-b坐标系，负载相电流a-b分量如图17所示，明显看出，死区存在时输出电流幅值下降且相位超前。

图17  负载相电流a-b轴分量波形

    在极坐标系，负载相电流长度与角度如图18所示，明显看出，死区存在时输出电流幅值下降且相位超前。 

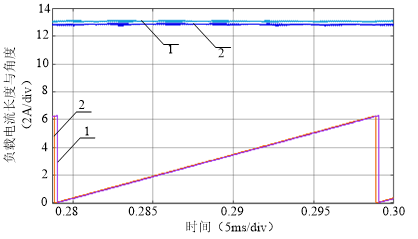
图18  负载相电流极坐标分量波形

    在d-q坐标系，负载相电流d-q分量如图19所示，明显看出，死区存在影响输出电流幅值的d-q分量分配。 

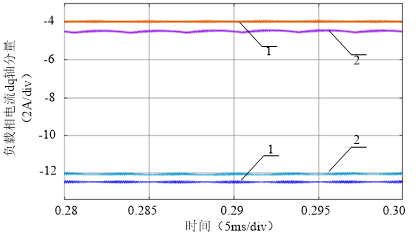
图19  负载相电流d-q轴分量波形

3.5 有死区对相位仿真分析

3.5.1 期望输出电压频率的影响（on delay）

    在以下仿真分析中，功率电路为3相VSI，直流电压为538.79V，负载为阻感串联负载5W+50mH，仿真步长1e-7s。

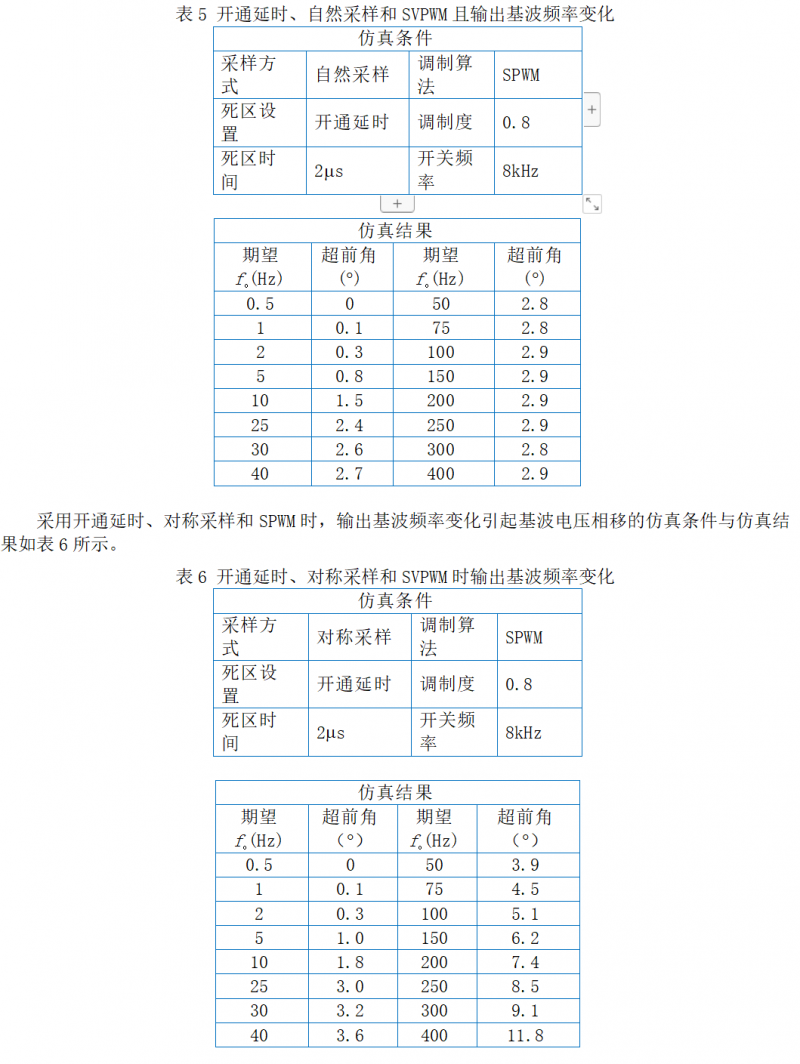
    采用开通延时、自然采样和SPWM时，输出基波频率变化引起基波电压相移的仿真条件与仿真结果如表5所示。

3.5.2 死区时间长度的影响（on delay）

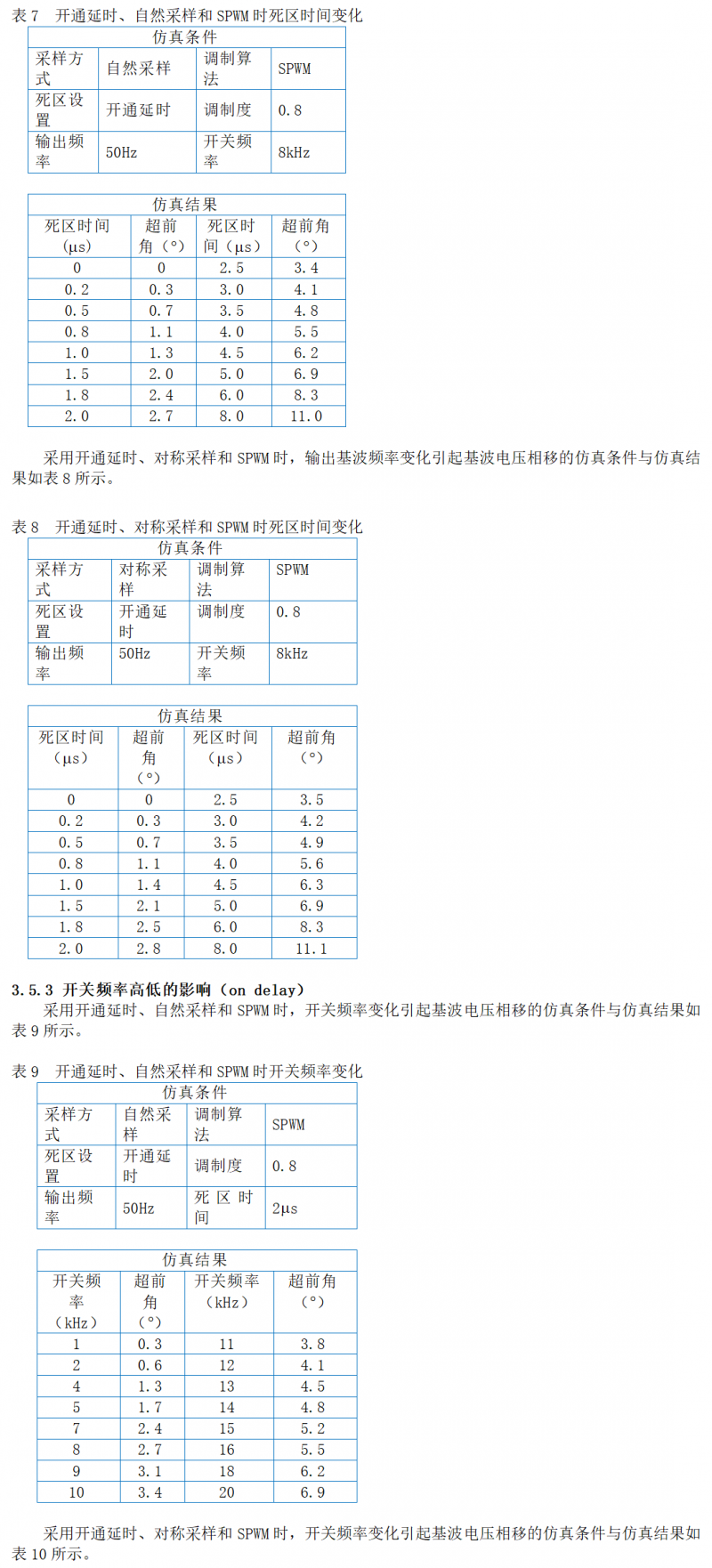
    采用开通延时、自然采样和SPWM时，死区时间变化引起基波电压相移的仿真条件与仿真结果如表7所示。

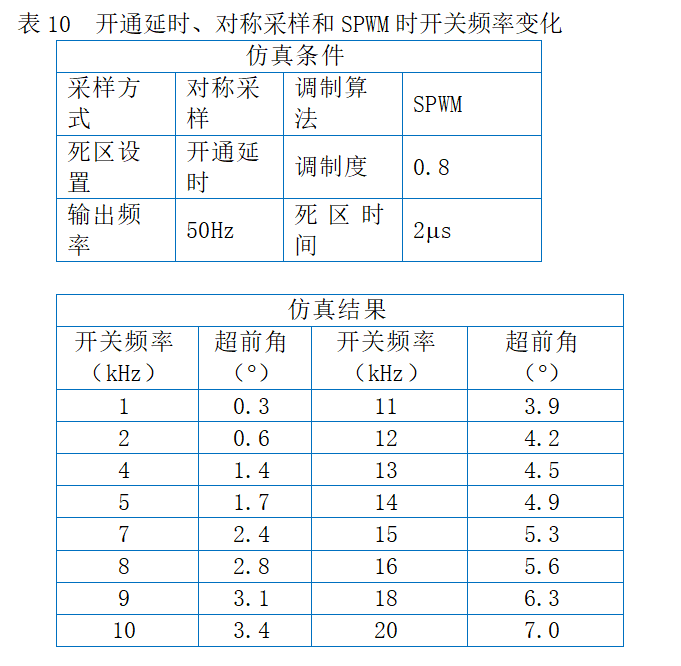
3.5.4 调制度高低的影响（on delay）                                                                                                                 

    采用开通延时、自然采样和SPWM时，调制度变化引起基波电压相移的仿真条件与仿真结果如表11所示。

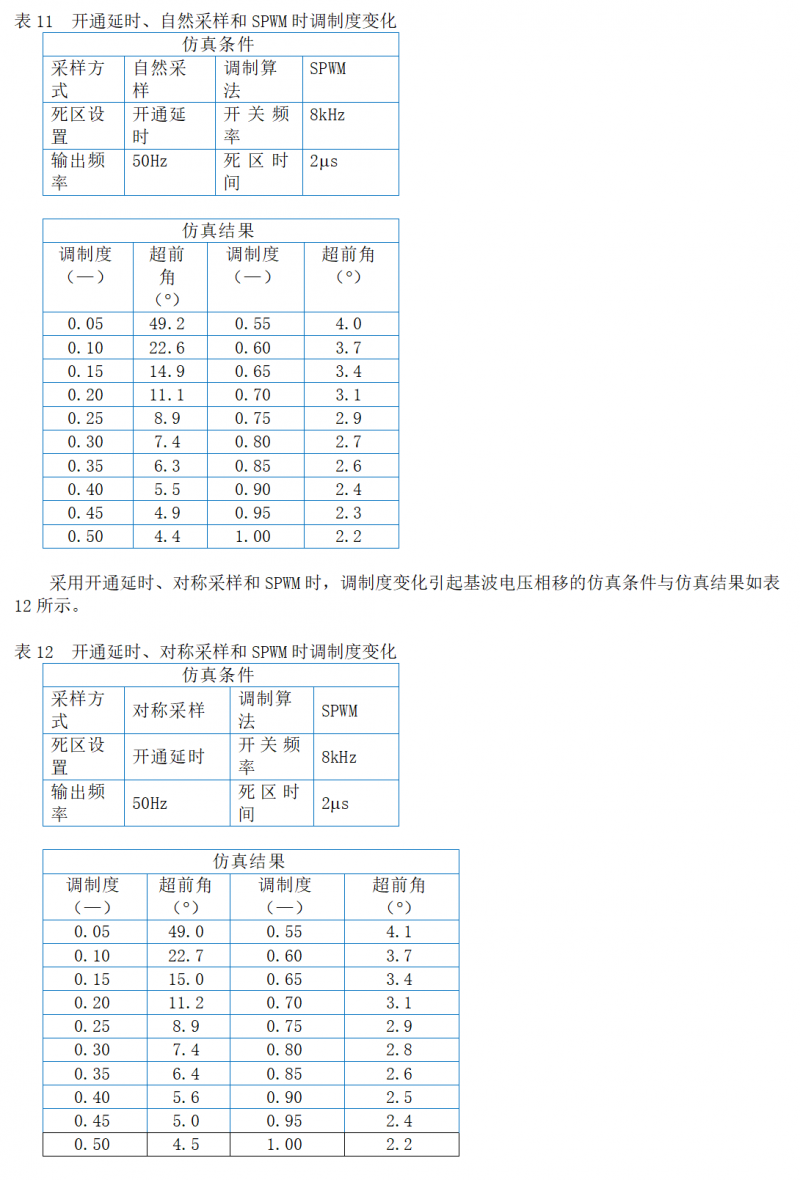
3.5.5  期望输出电压频率的影响（off delay）

    采用关断提前、自然采样和SPWM时，期望输出电压频率变化引起基波电压相移的仿真条件与仿真结果如表13所示。

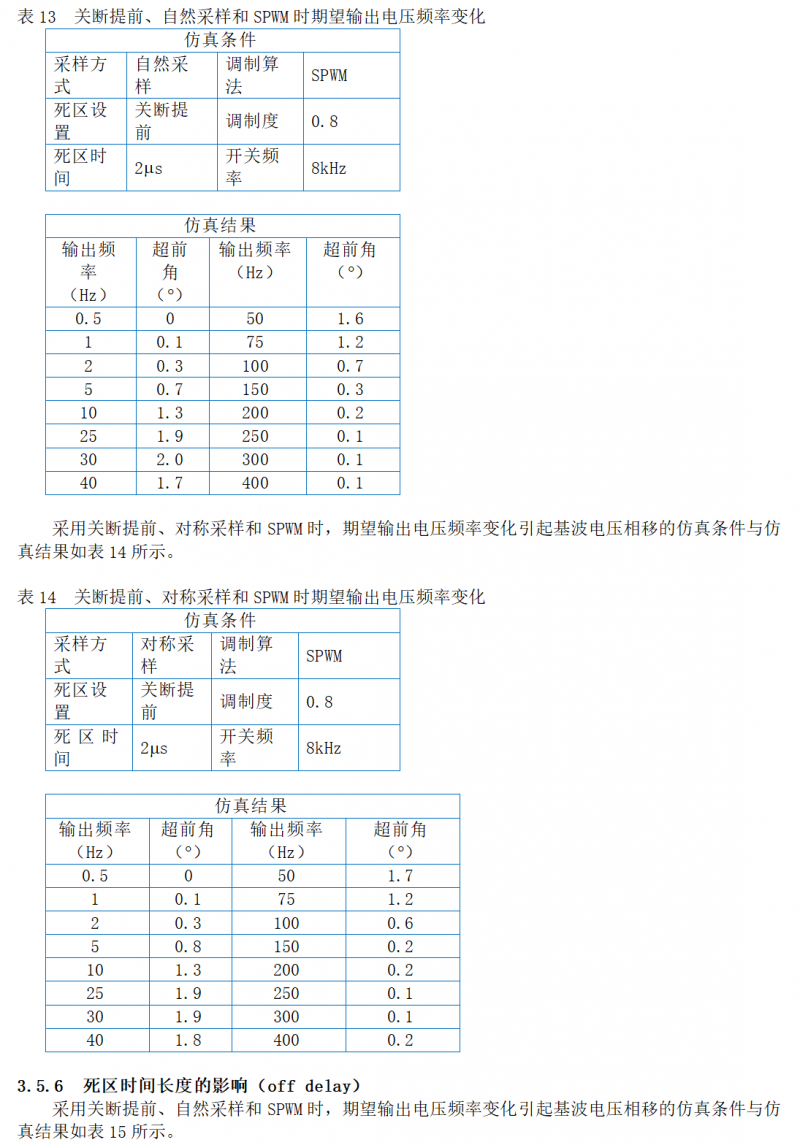
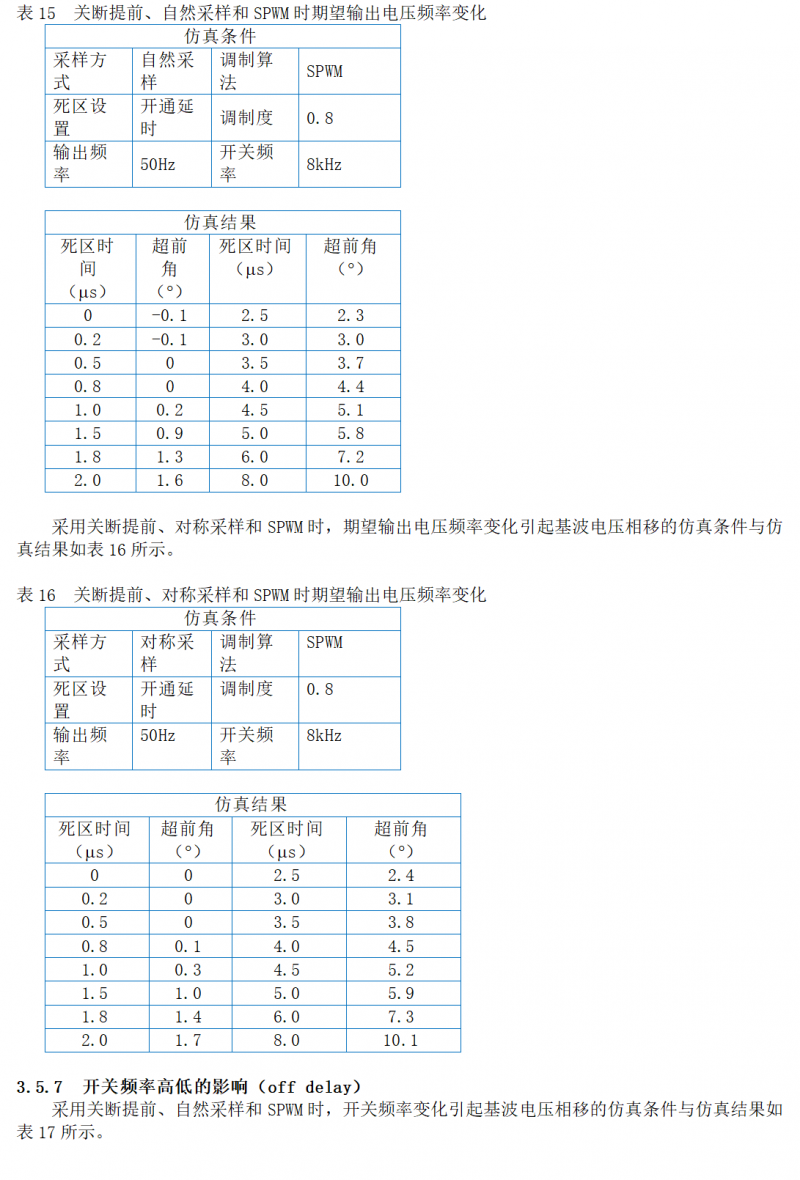
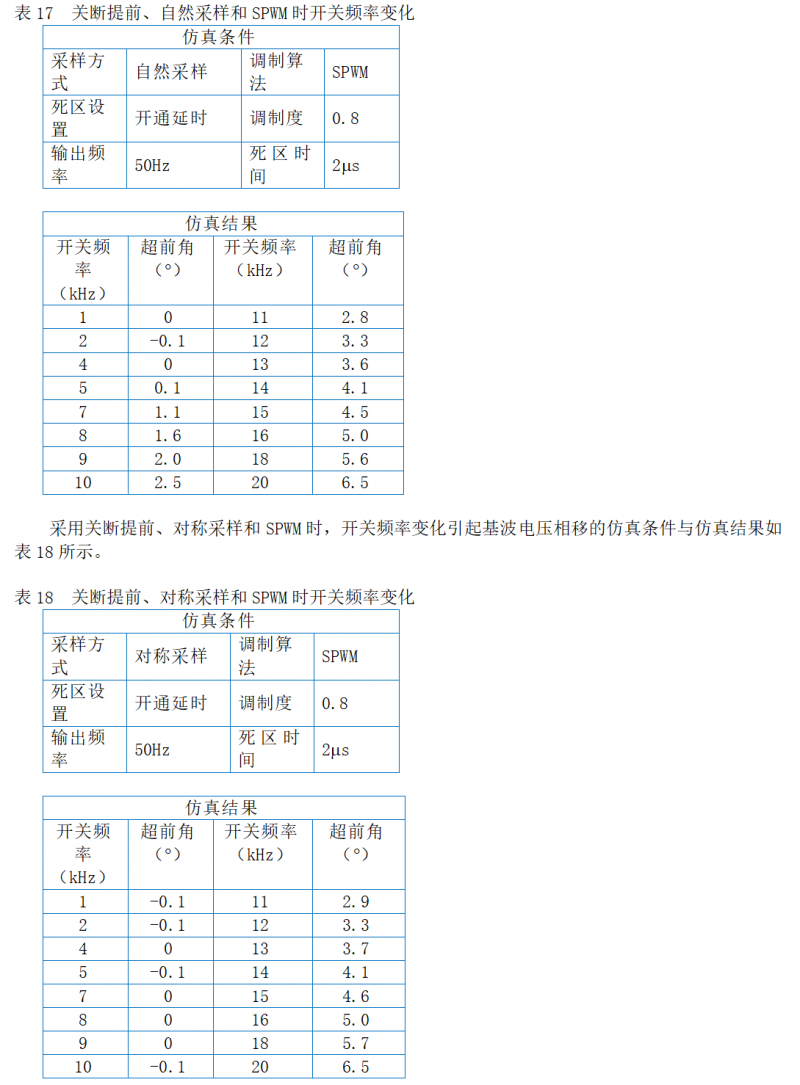
3.5.8  调制度高低的影响（off delay）

采用关断提前、自然采样和SPWM时，调制度变化引起基波电压相移的仿真条件与仿真结果如表19所示。

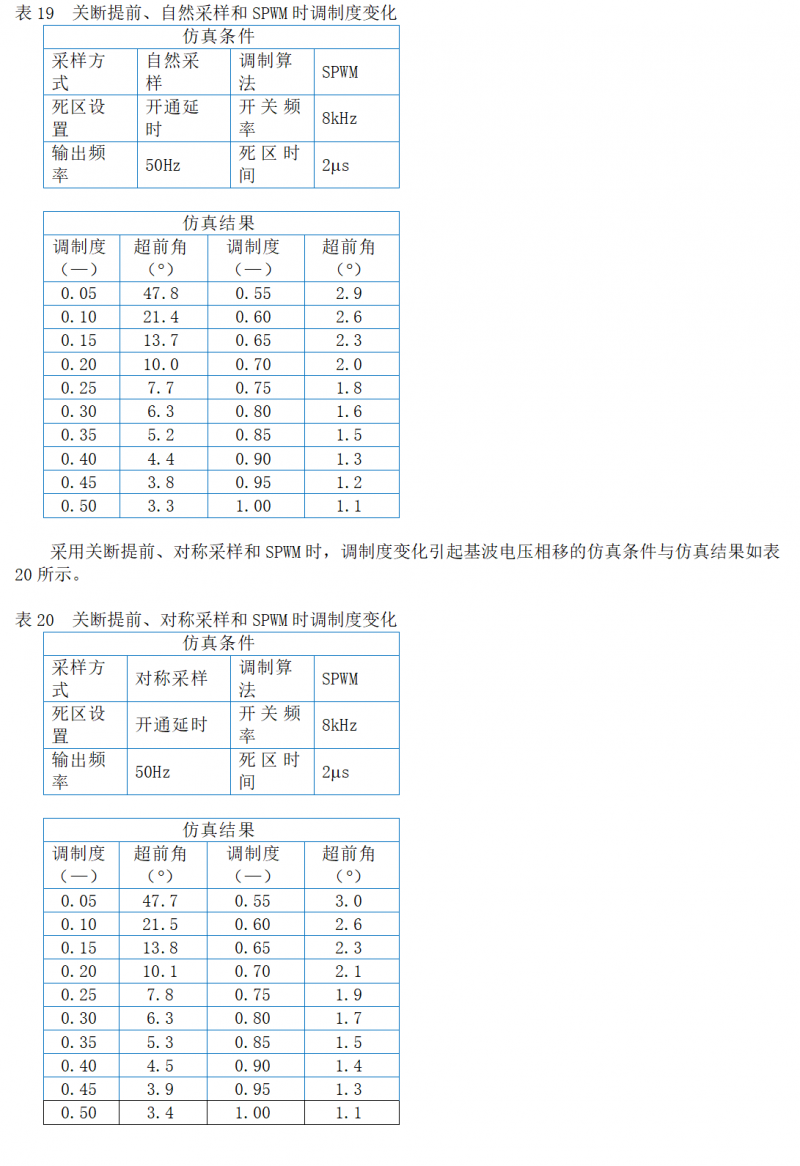
    通过以上仿真数据可知，无论采用开通延时或关断提前、自然采样或规则采样、SPWM或SVPWM，只要存在死区，输出基波电压就会产生超前相移。相移大小与期望输出电压频率、调制度有关。虽然以三相RL串联负载为例进行分析，该结论也适应于三相电动机负载。但是由于电动机具有反电势，因此死区时间对基波电压相位的影响应该略有改变。可以得出几个结论：（1）死区时间越长，影响越大；（2）负载越轻，影响越明显。

    此外，通过对ON/OFF死区设置方法的仿真分析，发现死区时间对逆变器-负载系统的基波电压幅值和相位没有影响。

    期望输出电压频率与调制度的变化反应了电动机工作频率、负载轻重的变化。一般PMSM传动系统需要对位置、转速进行闭环控制，如果存在死区引起的基波电压相移，原有的PMSM闭环控制系统无法进行自动补偿，为此需要设计改进的相位补偿控制策略。同时，也应该注意到，死区引起的基波电压相移的实时计算非常困难。

4  死区引起基波电压相移的补偿分析

4.1  传动系统的仿真分析

    三相VSI-PMSM传动系统仿真电路如图20所示^[18]，直流电压为300V，PMSM为凸极型，正弦波反电动势，直轴与交轴电感分别为0.02547H 和0.02816H，定子每相电阻18.7W，磁链0.1716V.s，角度为零时转子磁链定位90°滞后U相轴（修改Park），负载转矩1.7N.m，转动惯量J为2.26e-05 kg.m^2，粘滞阻尼F为1.349e-05 N.m.s、极对数p 为2，静止摩擦Tf为0N.m。期望运行转速3750rpm，相当于392.6990rad/s和运行频率125Hz。有无死区时PMSM稳态定子电流如图21所示，有无死区时PMSM转子角度及其差如图22所示，有无死区时PMSM转矩与转子转速如图23所示。

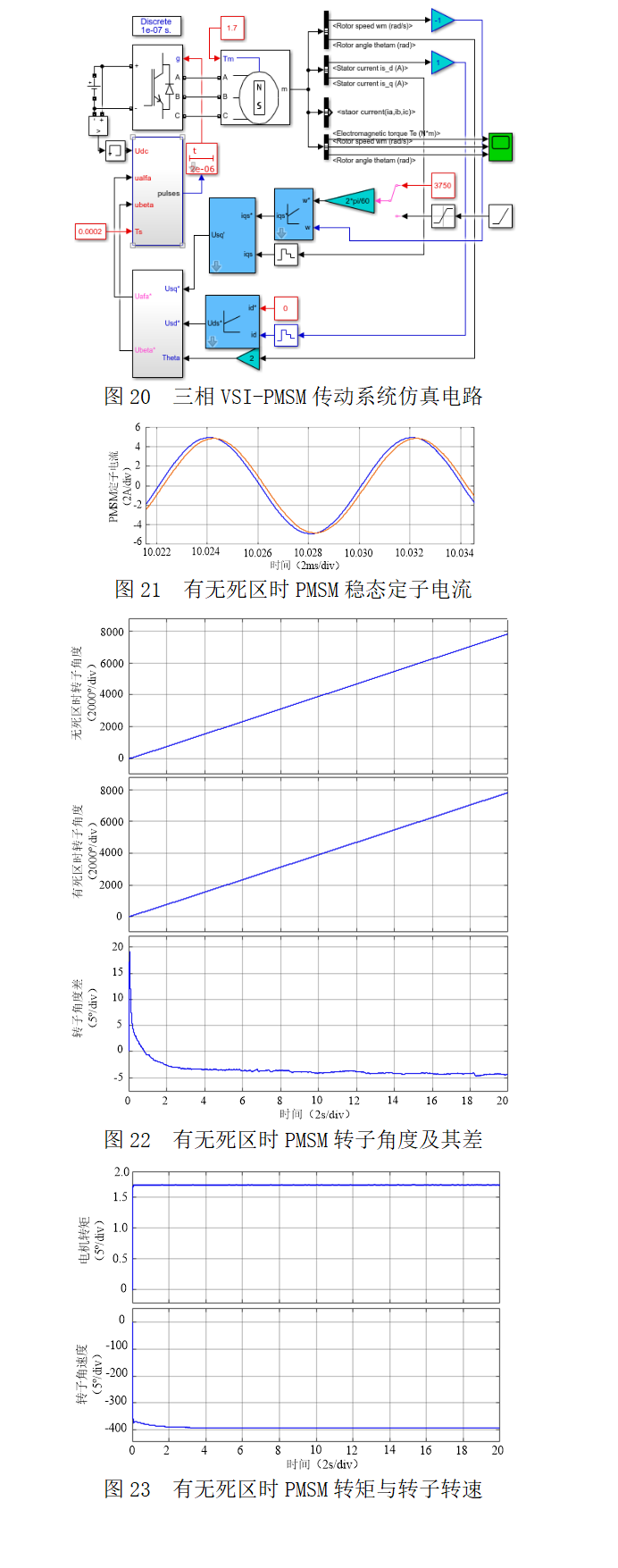
可以读出，有无死区时PMSM定子电流相位差为8.10°，转子位置差为4.35°，大致呈现2倍关系。

4.2  离线补偿法

    根据PMSM传动系统的整个运行条件，通过仿真分析方法，确定不同工况条件下的死区时间引起的基波电压相移角，绘制成表格，则可以采用查表法确定补偿角度。一种考虑死区引起基波电压相移的矢量控制PMSM传动系统如图24所示。图中，为死区时间引起的基波电压超前相位，即为期望的无死区影响的ab坐标系中的旋转矢量的相位。

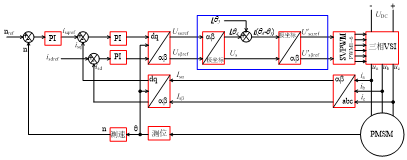
图24  死区相移补偿的PMSM传动系统

    对于三相并网VSI而言，虽然直流回路电压受到PV条件变化范围较大，但是由于网压网频比较固定，补偿方案中只需要特别考虑直流电压的波动，一种考虑死区引起基波电压相移的矢量控制PV逆变器并网系统如图25所示。

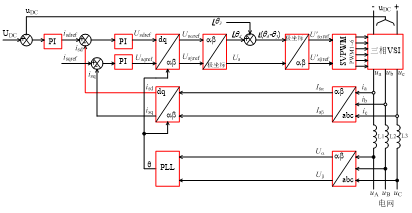
图25  死区相移补偿的PV并网传动系统

    图24与图25是在a-b坐标系下完成死区引起基波电压相移补偿，也可以采用SPWM算法在a-b-c坐标系下完成相移补偿。

    无死区时、有死区无相位补偿时、有死区有相位补偿时PMSM一相定子电流的幅相关系如图26所示。图中，“1”表示无死区情况，“2”表示有死区无相位补偿情况，“3”表示有死区有相位补偿情况。有死区有相位补偿时PMSM转子位置差如图27所示。可见，合适的相位补偿可以产生满意的相位补偿效果。

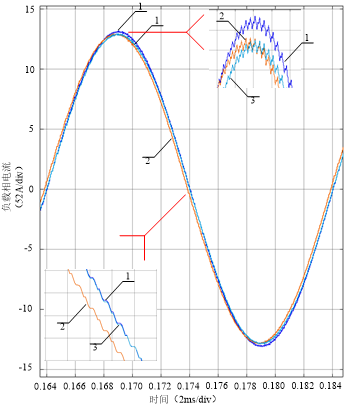
图26  无死区时、有死区无相位补偿时、有死区有相位补偿时PMSM一相定子电流的幅相关系

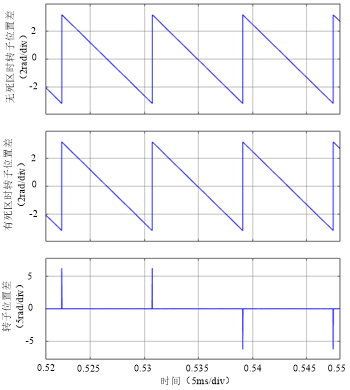
图27  有死区有相位补偿时PMSM转子位置差

4.3.2  恒调制度法

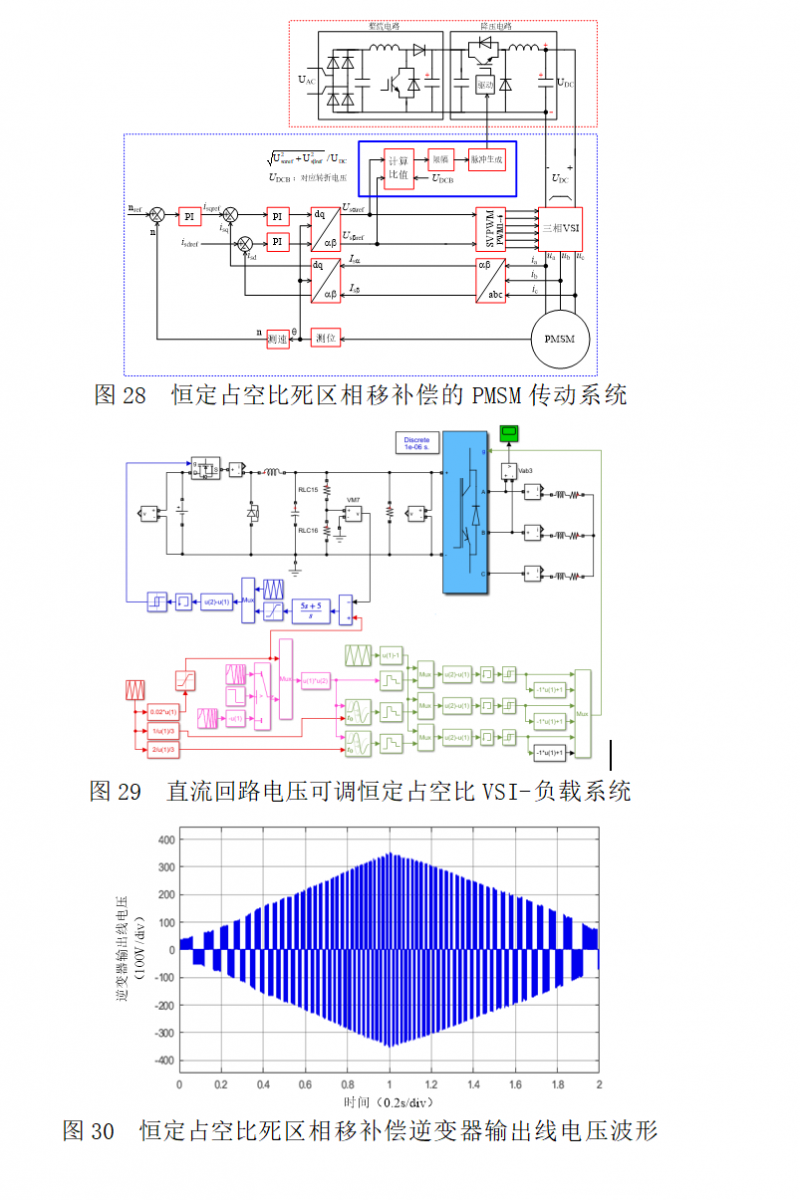
    针对电动机传统系统，可以根据电动机实际运行转速，实时调节直流回路电压，维持调制度恒定，这样传动系统中只有工作频率在变化，因此很容易获取死区时间引起基波电压相移的数值。一种便于死区引起基波电压相移补偿的、调制度恒定的矢量控制PMSM传动系统如图28所示，简化后的仿真电路如图29所示，图中，在恒转矩范围内，直流电压与输出频率成正比。当输出频率由小到大、再由大到小变化时，逆变器输出线电压波形如图30所示。可见，可以采用BUCK DC-DC变换器调节最终输出电压，在较大范围内实现PMSM传动系统的恒调制度，便于实现相位补偿。

5  结论

    针对三相VSI-阻感串联负载系统、三相VSI-PMSM传动系统进行仿真分析，确定开通延时、关断提前的死区设置方式均使得产生的输出电压基波相位超前，超前量与期望输出频率、开关频率、采样方式、调制方法、负载性质、调制度等因素密切相关。相位超前会引起闭环控制系统出现固定超前，属于固有偏差，对PMSM传动系统的精确相位控制产生影响，可以采取相位补偿控制策略。给出了两种相位补偿方法：离线补偿法和恒调制度法，并通过VSI-PMSM传动系统的仿真验证。本文工作有助于探索死区设置对输出基波电压相位影响，尤其对包括PMSM转子定位、PV并网发电以及无线输电在内的对相位和位置敏感的系统起到参考作用。

参考文献：

[1] 冯振东, 张力平, 周浩, 钦杰, 蔺宏良. 基于干扰观测器的逆变器在线死区补偿[J]. 机电工程技术, 2020, 49(02): 175-178.

[2] 罗赞如. 基于改进型内模控制的逆变器死区时间补偿[J]. 变频器世界, 2019(11): 110-113.

[3] 巩瑞春, 孙建国. 死区时间对三相SPWM逆变器直流母线纹波电流影响的研究[J]. 内蒙古农业大学学报(自然科学版), 2019, 40(06): 67-70+81.

[4] 李巍, 张津京. 基于电流过零区域检测的H桥逆变器死区补偿[J]. 甘肃科学学报, 2018, 30(02): 119-123.

[5] 刘和平, 路莹超, 王华斌, 苗轶如. 电压型逆变器分段死区补偿调制策略[J]. 电机与控制学报, 2018 ,22(03): 25-32.

[6] 袁林, 杨洪耕. 逆变器并联系统死区的环流效应及其抑制方法[J]. 水电能源科学, 2017, 35(09): 187-191.

[7] 罗辞勇, 王英豪, 王卫耀, 南航, 魏欣欣. 单相特定谐波消除脉宽调制高频逆变器的死区补偿策略[J]. 电工技术学报, 2017, 32(14): 155-164.

[8] 张鹏, 陈甜甜, 唐振东, 杨洪耕. 弱电网下考虑装置死区效应时的逆变器并网电能质量分析[J].水电能源科学, 2017, 35(06): 203-207.

[9] 谢晔源, 谢瑞, 李成敏, 周志超, 李武华. 计及寄生电容和纹波电流的电压源型逆变器死区效应与补偿方法[J]. 电工电能新技术, 2017, 36(06): 16-21.

[10] 范波, 徐翔. 应用于感应电机矢量控制中的逆变器死区补偿[J]. 计算机测量与控制, 2017, 25(02): 70-73.

[11] 程世超, 刘彦呈, 郭昊昊. 基于SVPWM的逆变器死区效应分析与补偿[J]. 微特电机, 2016, 44(10): 86-88+100.

[12] 赵乐, 曹以龙, 江友华. 三相并网逆变器的一种新型死区补偿方法[J]. 电力电子技术, 2016, 50(09): 41-43.

[13] 张展, 高照阳. SVPWM逆变器死区补偿中的电流极性检测[J]. 大连工业大学学报, 2016, 35(05): 386-390.

[14] 程小猛, 陆海峰, 瞿文龙, 张星, 樊扬, 伍理勋, 蒋时军. 用于逆变器死区补偿的空间矢量脉宽调制策略[J]. 清华大学学报(自然科学版), 2008(07): 1077-1080.

[15] 陈国呈. PWM变频调速及软开关电力变换技术[M]. 北京: 机械工业出版社 2001年04月.

[16] 陈国呈. PWM模式与电力电子变换技术[M]. 北京：中国电力出版社. 2016年09月.

[17] 陈国呈. 新型电力电子变换技术[M]. 北京：中国电力出版社. 2004年09月.

[18] 袁登科，徐延东，李秀涛. 永磁同步电动机变频调速系统及其控制[M]. 北京：机械工业出版社，2018.

------------------------------------------------------------------------------------------------------------------------------------------------------------