关键词:计算机仿真技术;谐波;LC滤波器
Abstract: A design solution of harmonic filter is presented in this paper. A filter is designed, a simulation mode of the system is developed by using the software SABER, the simulation results verified the rationality of the design. Based on the design and simulation results, an experiment prototype is manufactured. The property of the system and the effect of harmonic suppression is proven with the results of the experiment. Computer simulation technology is not only beneficial to theoretical study and teaching, but also has practical significance in engineering practices.
Key words: Computer simulation technology; Harmonic; LC filter
1 引言
谐波污染的危害众多,电力系统中存在谐波在发电、输电、变电、配电等环节都会影响效率,有可能引起谐振,还可能因造成保护装置误动作导致计量混乱的后果,谐波会使用电设备过热,缩短设备的正常工作寿命,谐波提高故障发生率,危害到系统的稳定性与可靠性,谐波还会严重干扰通信设备和电子设备。因此谐波抑制技术是环保节能的绿色技术,具有长远而重要的意义。
计算机仿真技术越发广泛地应用在电力电子技术的研发上,以目前的仿真技术水平,仿真结果精确性足够高,具有极高的参考意义。在研发中合理运用计算机仿真,可以缩短研发周期,降低研发成本,提高开发水平。目前主流仿真软件有PSPIC、MATLAB、SABER等。PSPIC较适合小功率场合,MATLAB精确性较差,而SABER不仅有型号丰富的器件库,还可建立个性化的元器件仿真模型,进行系统级的混合信号仿真,运算速度快,精确度高,仿真结果更接近实际运行情况。
本文对全桥逆变器的LC滤波器进行了合理的设计,并建立SABER仿真模型对设计进行了验证与优化。在保证输出电压质量与系统性能的前提下,LC滤波器的电感值与电容值越小,越有利于系统体积和重量的减小,以此获得更高的功率密度。
2 LC滤波器设计
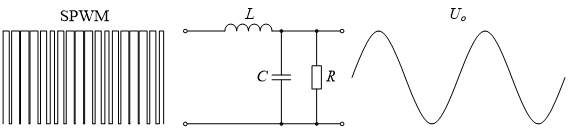
由于电流跟踪速度、电感电流纹波的大小与LC滤波器其中的电感值有关,所以设计LC滤波器时应综合考虑滤波电感、电容值的大小:减小滤波电感值,系统的动态性能变好,电感体积变小,但滤波电容值将增大。在相同的输出电压时,滤波电容增大意味着滤波电容电流增大、输出无功功率增大、效率降低。而增大滤波电感,虽然可以减小滤波电容值,但系统的动态性能变差,还会引起较大的噪声干扰。图1是二阶LC滤波器的功能示意图。
|
|
桥臂输出电压到滤波后输出电压的传递函数:
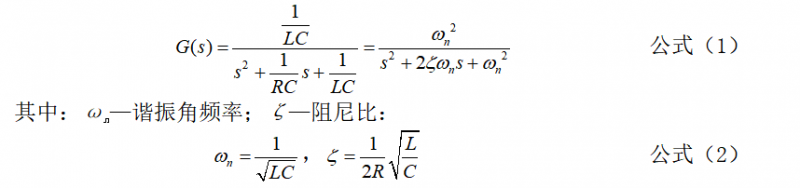
画出此二阶表达式G(s)的图形如图2所示。
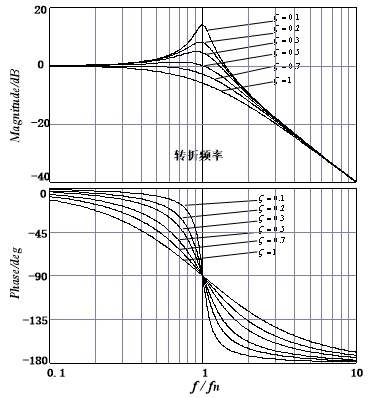 图2 二阶LC低通滤波器频率特性 |
本文滤波器设计的目的是通过低频信号,尽可能滤除开关频率处的谐波,转折频率fn的取值应满足fo << fn << fs,其中基波频率fo=400Hz,开关频率fs=80kHz。
2.1 满足滤波效果要求的最小电感值
取输出电流峰值的50%作为最大纹波电流的大小。额定输出功率1kW,额定输出电压115V,频率400Hz,则可以计算出最大纹波电流:
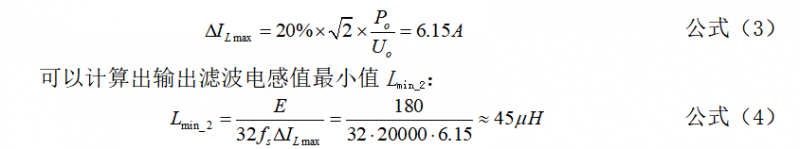
2.2 转折频率fn
对于输出电压的高次谐波的幅值Uoj(s),可将电阻R当作开路,则有:
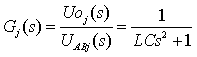 公式(5)
公式(5)
其中,j表示谐波次数。
如果4K±3次谐波的最大含量为Q%基波成分,要求输出电压中各次谐波含量小于A%基波成分,必然有Q/A>1,则对4K±3次谐波有以下关系:
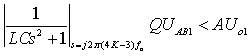 公式(6)
公式(6)
其中:UAB1是滤波前电压uAB的基波幅值;Uo1是滤波后电压uo的基波幅值。
设计滤波器时,通常使滤波电感上的基波电压降远远小于Uo1。额定负载电阻为R,令滤波电感上的基波电压幅值为Uo1的1/N。此外,为了减小无功容量,滤波电容容抗必须远远大于R。假设滤波电容容抗远远大于R(计算出电容值后可进行验证),即可得电感值近似为R的1/N,如公式(7):

其中,K=fs/fo=50,Q为4K-3次谐波在电压调制比M =0.8时的谐波含量,Q=14.3%,因此只要知道A的值,即可求出转折fn的值。
已知4K±n次谐波含量最多,4Km±n次谐波含量约为前者的1/m。经过滤波器4K±n次谐波衰减的幅度大约是4Km次谐波的1/m2倍,所以输出电压uo中4K±n次谐波含量近似是4Km±n次谐波含量的1/m3。因此,如果要满足THD不超过2%,输出电压uo中4K±n次谐波含量与THD的关系可推导如公式(12):
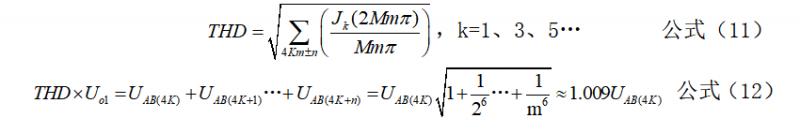
理论上可以计算出,电压调制比M=0.8时,4K±n次的谐波含量为31.4%,4K-3次的单次谐波含量为14.3%,则4K-3次谐波含量与总谐波含量的比值约如式

综合考虑,fn < 19.2kHz和fo << fn << fs(其中基波频率fo=400Hz,开关频率fs=80kHz),取fn=8kHz,根据公式(4)算出的滤波电感最小值,以及参考仿真结果与实验结果优化后最终选定滤波参数:L=60μH,进而算出C=6.8uF。
3 LC滤波器仿真结果
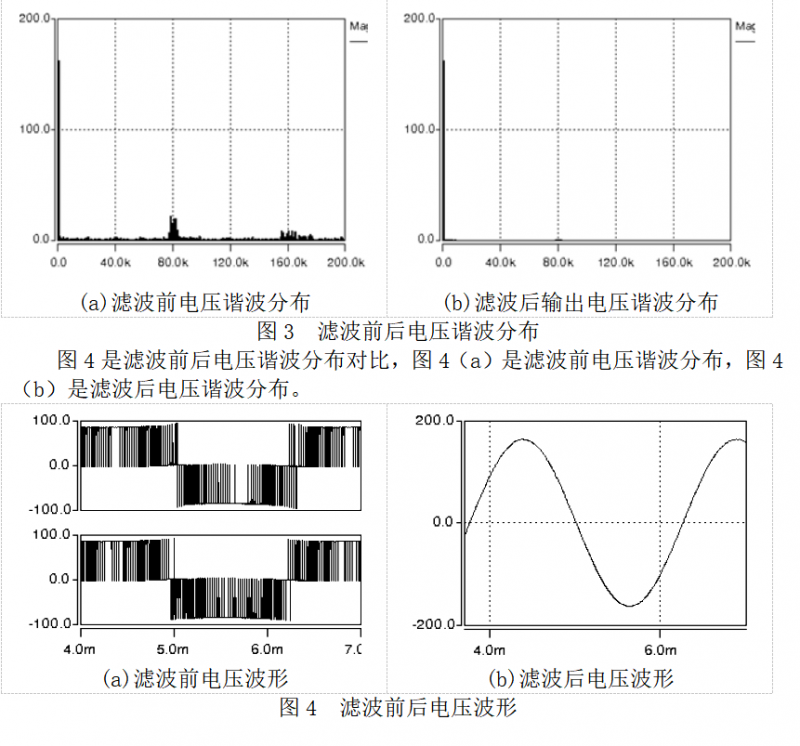
滤波器参数为L=60μH,C=6.8uF,阻性负载满载工作状态下系统SABER仿真结果如下。图3是滤波前后电压谐波分布对比,图3(a)是滤波前电压谐波分布,图3(b)是滤波后电压谐波分布。
|
|
|
4 LC滤波器实验结果
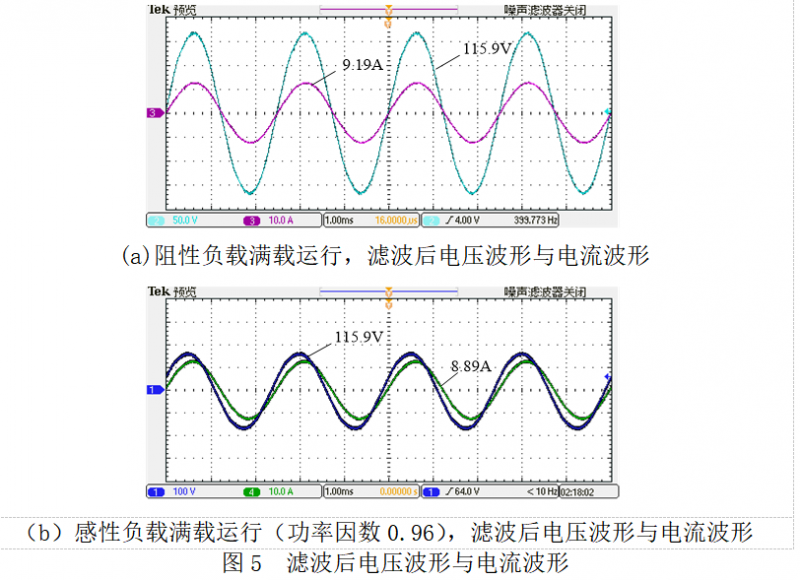
滤波器参数为L=60μH,C=6.8uF,满载工作状态下系统SABER仿真结果如下。图5是滤波后电压波形与电流波形,图5(a)是阻性负载情况,图5(b)是感性负载情况。实验结果测得滤波后THD=0.712%,且系统动态响应较快。
|
5 结束语
本文介绍了一种有效抑制谐波含量的滤波器的设计思路,设计了一款滤波器,基于SABER仿真软件建立了系统的仿真模型,仿真结果验证了设计的合理性,在此基础上搭建了实验样机,实验结果证明了系统的性能和LC滤波器抑制谐波的效果。计算机仿真技术不仅有利于理论研究和教学,在应用上也具有实际意义。
参考文献:
[1]何亮,王劲松. 三相PWM逆变器输出LC滤波器设计方法[J]. 电气传动, 2013(12):33-36
[2]俞杨威,金天均,谢文涛,吕征宇. 基于PWM逆变器的LC滤波器[J]. 机电工程, 2007(05): 50-52
[3]曹立威,吴胜华,张承胜,吴保芳. SPWM谐波分析的一般方法[J]. 电力电子技术, 2002(04): 62-65
作者简介:
王雪钰(1988-),女,江苏南京人,讲师,硕士研究生,从事高压大功率变换器等方面的研究。
项目支持:
南京铁道职业技术学院青年科研基金项目,带有源PFC的工业电源的研究(项目号YQ180024)







共0条 [查看全部] 网友评论