关键词：双三相；永磁同步电机；比例谐振；矢量控制

Abstract: At present, for the two-phase three-phase permanent magnet synchronous motor, the traditional current vector control strategy mostly adopts the d-q component in the synchronous rotating coordinate system for feedforward decoupling PI control. This traditional vector control technology not only requires complex rotational coordinate transformation calculation, but also the motor's inductance, resistance, and other motor parameters change with the saturation of the magnetic circuit and the temperature rise during the operation of the motor, thus making the cross coupling terms are inaccurate, resulting in reduced control accuracy. In this paper, a current vector control strategy based on proportional resonance control in a stationary coordinate system is proposed. The control effect is the same as that of the PI controller in the synchronous coordinate system. It can track the sinusoidal signal of a specific rated frequency without a steady-state error. The harmonics are selectively compensated. Compared with the traditional PI control method, the vector control system based on the PR controller in the stationary coordinate system does not contain the feedforward compensation term and the decoupling term related to the motor parameters, which reduces the coordinate transformation and thus reduces the control algorithm. The difficulty of implementation increases the robustness of the control system.

1  引言

随着社会的发展，电力电子技术的进步，多相电机以它独有的优势越来越备受大家关注，相对于传统的三相电机，多相电机有以下几个优点：

（1） 可运用于大功率的场合。相对于三相电机，多相电机对电力电子器件的功率要求较低，在某些大功率场合下，三相电机有时满足不了电力电子器件的功率要求^[1-2]。

（2） 转矩脉动较小，静态特性和动态特性相对较高。三相系统中，5次谐波的存在使系统产生6次转矩脉动，影响系统的静、动态特性。然而在多相系统中，特别是用双三相电机，5次和7次谐波被消除，脉动频率也有所提高，转矩脉动大幅度下降^[2-3]。

（3） 系统整体的可靠性提高。当多相系统的某一相出现故障停止工作，可以有一系列的补救措施，从而不用系统停止工作，在某些场合下可降低不必要的损失^[4-5]。

双三相永磁同步电机是人们目前研究最为广泛的一种，它的定子是由两套对称的三相绕组构成，这两套三相对称绕组分别采用Y型连接并且在空间上相差30度电角度，每套Y型连接的内部绕组在空间上互差120度，构成一个不对称的六相系统，从内部看是一个绕组对称的12相系统，其结构如图1所示。这种结构的双三相电机基波电流消除了5次和7次谐波，产生的最低谐波磁势为11次和13次，从而使转矩脉动的次数提高到了12次，即减少了双三相电机的转矩脉动，提高了电机的性能^[6]。

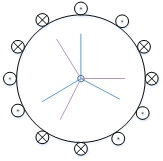
图1  双三相永磁同步电机内部结构模型

目前对这种双三相永磁同步电机的建模方法主要有两种。一是完全按照三相电机的建模方法，把双三相永磁同步电机看作两个独立的三相电机分别进行建模，这种方法叫做双d-q变换法。这种建模方法也同样适用于9相和12相电机。二是将这双三相电机看作一个整体，利用矢量空间解耦的建模方法，将各个变量分解到基波子空间和各谐波子空间中，各子空间的分量对能量转换和系统功耗有着不同的作用^[7]。本文采用第二种建模方法，即矢量空间解耦的建模方法对双三相永磁同步电机建立数学模型。采用矢量空间解耦坐标变换方法，可以将DTP-PMSM的各变量分别映射到几个彼此正交的子空间，即参与机电能量转换的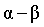基波子空间，以及不参与机电能量转换的谐波子空间和零序子空间，其中零序子空间可以忽略，谐波次谐波需要被有效抑制^[8]。

DTP-PMSM控制系统的电流控制部分一般采用旋转参考坐标系下的比例积分(PI)电流控制，PI电流控制由于增益和带宽限制，难以对交流信号实现无静差跟踪控制。而静止参考坐标系下的比例谐振(PR)电流控制不含与电机参数有关的项，既能够减少复杂的旋转坐标变换计算，也能够无稳态误差地跟踪特定频率的正弦交流信号^[9]，故可用其代替PI电流控制。

2  双三相永磁同步电机的建模

为了得到简化、易于仿真和分析的模型，和三相永磁同步电机一样，对双三相永磁同步电机做如下假设：（1）定子电流和转子永磁体产生的气隙磁链都看作正弦分布；（2）忽略铁芯磁饱和效应以及涡流、磁滞损耗；（3）忽略绕组间的互漏感。

2.1  双三相永磁同步电机在自然坐标系下的方程

在六相自然坐标系下，双三相永磁同步电机的电压方程和磁链方程分别如下：
   

三相电机可以通过Clarke-Park变换矩阵将各变量分别映射到按转子磁场定向的d-q-0坐标系下，得到相互解耦的d、q轴磁链方程和仅与d、q电流有关的电磁转矩表达式，简化了系统的结构。而且当三相电机定子绕组的中性点不与逆变器相连时，0轴的各分量都为零，从而得到本质上为三阶的三相电机模型。双三相电机两套三相绕组的中性点相互隔离，相当于有两个电流约束条件，所以其本质上应该是一个五阶系统。通过合适的坐标变换可以将它映射到一个四轴坐标系下，得到更为简单的表达式^[10-11]。

2.2  基于空间矢量解耦坐标变换的数学模型

Yifan Zhao和T.A.Lipo等人通过空间矢量解耦的方式，将DTP-PMSM在自然坐标系下的各个变量转换到六相静止坐标系，变换矩阵Ts为
  

若非特别说明，本文后面提到的PR控制器皆是指准PR控制器，两者之间不再加以区分。

    基于PR控制器的双三相永磁同步电机的控制框图如图2所示。

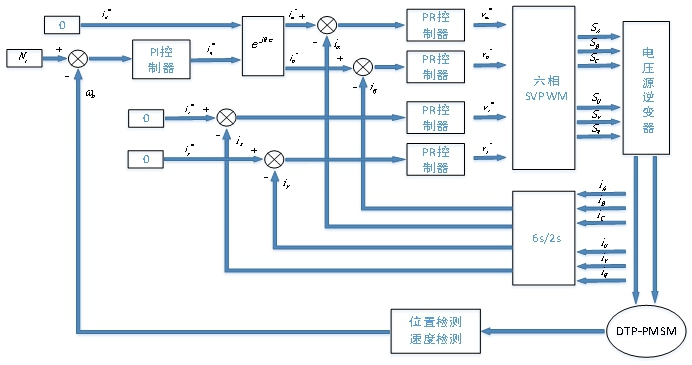
图2  基于PR控制器的双三相永磁同步电机的控制框图                                                   

传统的基于PI电流控制器的双三相永磁同步电机的速度控制系统能够良好的实现速度控制和位置控制，是一种非常成熟的解决方案，广泛应用于实际工程场合，但这种传统的矢量控制技术需要复杂的旋转坐标变换计算，而且电机在运行中，电机的电感、电阻、等电机参数会随着磁路的饱和、温度的升高而发生改变，从而使交叉耦合项不准确，导致控制精度下降。本文介绍的基于PR控制器的双三相永磁同步电机控制系统不含与电机参数有关的前馈补偿项和解耦项，减少了坐标变换，从而减小了控制算法的实现难度，提高了控制系统的鲁棒性。

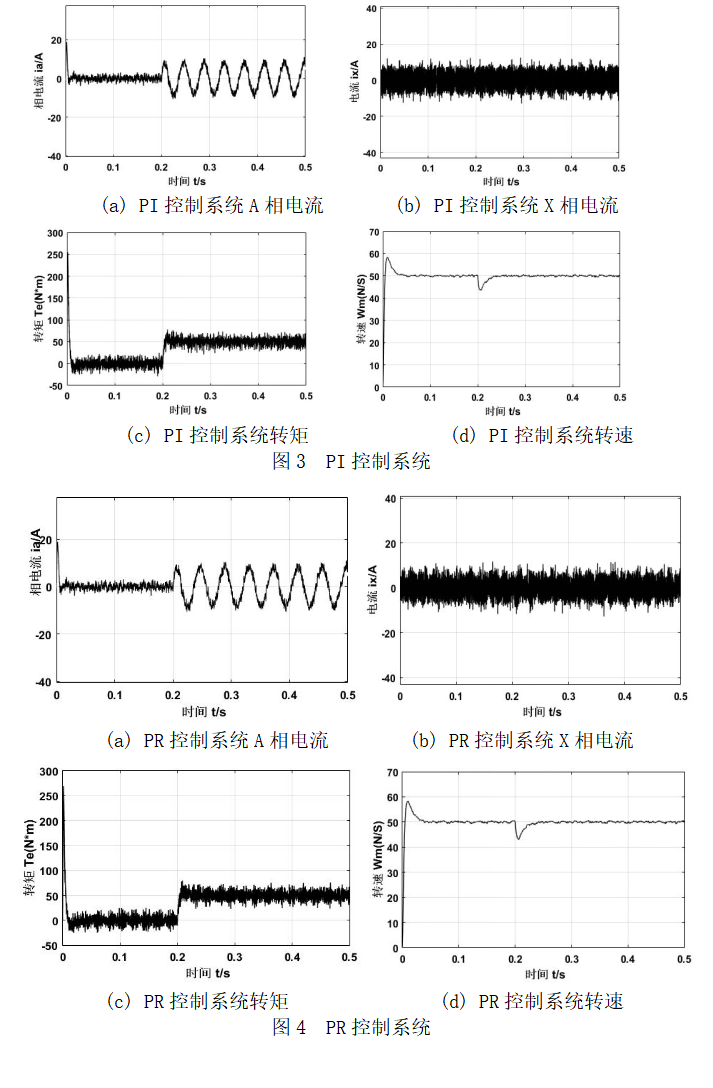
在额定转速以及随后突加负载转矩的条件下，给出传统PI控制系统和基于PR控制系统的A相电流、X相电流以及转矩和转速的仿真结果如图3和图4所示，由此可见，它们能达到相同的控制效果。

  

6  结论

本文对PR控制器设计做了详细的描述，以及与传统基于PI控制器的控制系统做了相应的比较，发现加入PR控制器后的控制系统可以在静止坐标系下实现对交流信号的无静差调节，减少的一次坐标变换，同时省去了耦合项和前馈补偿相，大大简化了控制系统，增强了控制系统的鲁棒性，且能达到与PI控制系统同样的控制效果，仿真实验证明了这一点。

参考文献：

[1]王铭．双三相永磁同步电机直接转矩控制的研究[D]. 长沙:湖南大学电气与信息工程学院，2010: 1-4．

[2]张敬南． 船舶电力推进六相同步电动机控制系统研究[D]. 哈尔滨: 哈尔滨工程大学自动化学院，2009: 8-10．

[3] BOJOI Ｒ，LAZZAＲI M，PＲOFUMO F，et al． Digital field-oriented control for dual three-phase induction motor drives[J]. IEEE Transactions on Industry Applications，2003，39(3): 752-760．

[4]LEVI E，BOJOI Ｒ，PＲOFUMO F，et al． Multiphase induction motor drives-a technology status review [J]. IET Electric Power Applications，2007，1( 4) : 489-516．

[5]薛山． 多相永磁同步电机驱动技术研究[D]. 北京: 中国科学院电工研究所，2006: 13-14．

[6]章玮,陈伯建,张平. 双三相永磁同步电机谐波电流抑制技术[J]. 电机与控制学报,2015,19(01):23-28.

[7]BOJOI R，LAZZARI M，PROFUMO F，et al． Digital field-oriented control for dual three phase induction motor drives[J]. IEEE Transactions on Industry Applications，2003(3): 752-760．

[8] ZHAO Yifan，LIPO T A． Space vector PWM control of dual three-phase induction machine using vector space decomposition[J]. IEEE Transactions on Industry Applications，1995，31 (5): 1100-1109．

[9] ZMOOD D N, HOLMES D G, BODE G H. Frequency do-main analysis of three-phase linear current regulator [J]. IEEE Transactions on Industry Applications, 2001, 37(2):601-610.

[10]卢峥，欧阳红林，孟超，等．多电平双Y移30°永磁同步电机的矢量控制系统[J]． 电工技术学报，2016，31(22)：45-56．

[11]Che H S, Levi E, Jones M, et al. Operation of a Six-Phase Induction Machine Using Series-Connected Machine-Side Converters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1):164-176.

[12]欧阳红林． 多相永磁同步电动机调速系统控制方法的研究[D]. 长沙: 湖南大学电气与信息工程学院，2005: 11-38．

[13]张刚. 基于PR控制的永磁同步电机SVPWM仿真研究[J]. 自动化技术与应用,2019,38(06):6-10.

[14]卫国岗,孙世宇,刘金宁. 基于准PR控制的逆变器优化控制[J]. 国外电子测量技术,2017,36(11):80-84.

[15]罗德荣,陈自强,黄守道,郭灯塔. PR控制器在永磁同步电机控制中的应用[J]. 湖南大学学报(自然科学版),2013,40(03):59-64.

作者简介：

朱强，1994,01,09，男，硕士研究生，研究方向：电力电子与电力传动。