1  引言

OFDM（Orthogonal Frequency Division Multiplexing，OFDM）系统作为当下通信系统中应用最广泛的技术之一，能够实现数据的高速传输。通过将深度学习技术嵌入到OFDM系统中对于之后MIMO-OFDM（Multiple-Input Multiple-Output-OFDM）系统以及大规模MIMO系统有着重要意义。

当下OFDM系统信道估计技术并非完美。其中最小二乘法（least squares，LS）得益于其算法简单方便，应用最为广泛。但是同时由于LS算法受到多径效应的影响导致导频处信道频域响应信息不准确，局限了算法的应用场景。线性最小均方误差(linear minimum mean square error，LMMSE)，由于其在信道估计过程中必须获取信道的统计信息，也使得算法难以普遍应用。在系统信道估计过程中，可以得到信道可以建模成自回归过程，所以系统信道估计的问题也可变为求取自回归系数的过程^[1]。

深度学习方法在解决非线性问题上表现良好，故而在此使用一种基于一维卷积神经网络（one dimensional CNN，1D-CNN）的OFDM信道估计方法。深度学习理论中神经网络的训练在获取神经网络输出的过程中可以无限逼近最优值，另外在神经网络输入混杂噪声的数据可以获取信道数据的分布，可解决噪声的困扰，最后神经网络在输入为离线信道数据时可以获取信道特征分析得到信道变化^[2]。

2  系统模型

假设OFDM系统中总共由L条信道路径，在信道数据传输过程中，多径时延为。OFDM系统的系统模型可如图1所示：

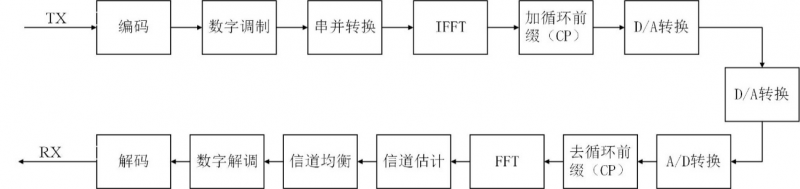
图1  OFDM通信系统

提出基于深度学习的OFDM系统下的信道估计的总的系统结构图如图2所示。通过传统信道估计方法得到导频处的信道频域响应作为神经网络的数据集，之后神经网络通过数据集做迭代训练，在得到最优的神经网络模型之后，应用到OFDM系统当中进行在线的信道估计。

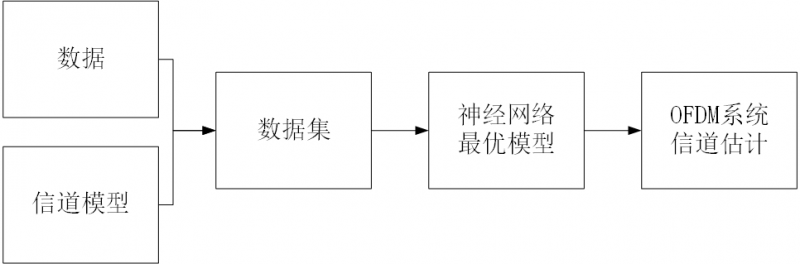
图2  系统结构图

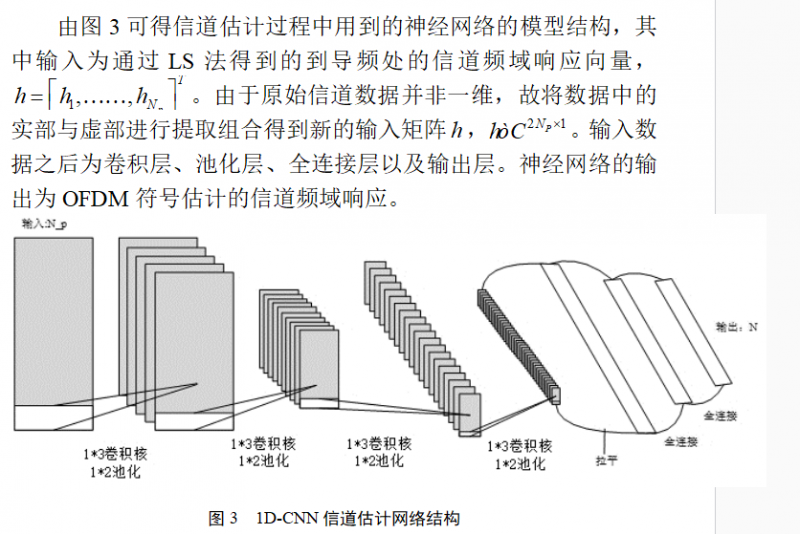
3  模型结构与训练过程

与ReLU激活函数的具备共同的性质在处理网络训练过程中产生的过拟合现象，通过该激活函数也能够有效避免。在神经网络中间部分的卷积层中卷积核的大小为，通过将卷积核设置为如此，可使网络中下层卷积层有丰富的可调参数，卷积层后紧跟池化层，对数据做简化，降低算法复杂度^[7]。在经过网络所有的卷积层之后会转变为DNN中的全连接层，将卷积层得到的所有输出转变为全连接层的输入。如DNN一样每层全连接层之间的神经元通过激活函数链接。

卷积层之后导致开始的全连接层神经元数目陡然增加，故在此使用dropout策略避免过拟合以及减小算法复杂度。如图5展示了神经网络在经过dropout之后网络的训练过程，图5（b）中的点式线构成的神经元为通过dropout之后过滤掉的，1D-CNN中全连接处的dropout参数设置为0.6。最后神经网络全连接层数为3层，输出层的神经元数目为OFDM符号估计的信道频域响应，即N。

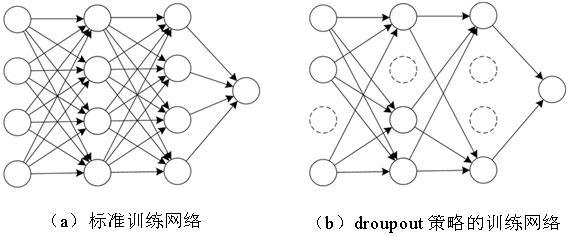
图5  droupout策略对比

4  仿真分析

如图2所示1D-CNN共有4层卷积层3层全连接层。在全连接层中设置全连接层的神经元各位为1024，1024，50，中神经网络的输入响亮的长度，总共集取10000个样本数据，其中训练集为8000，测试集为2000。因为采用的Adam算法进行参数更新，损失值的下降速度极快，因此设置初始学习率为0.01。

OFDM系统中信号的载波频率设置为2.8Gz，系统带宽为5MHz。信号的调制方式为4QAM，采用瑞利信道模型。其中子载波数与导频子载波数为25，250。多径时延以及路径增益有。本节将1D-CNN算法与LS算法以及LMMSE算法进行比较其误码率性能如图6所示。

图6  1D-CNN与其他信道估计方法BER对比

通过图6中1D-CNN与其他信道估计方法BER（Bit Error Ratio，BER）对比曲线可以看出，信号SNR增加后，在高信噪比状态下1D-CNN信道估计方法与LS以及LMMSE方法相比其误码率更低。

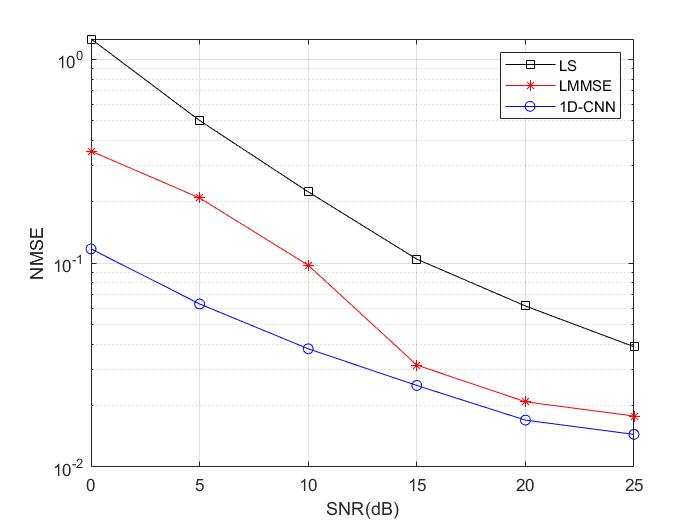
图7  1D-CNN与其他信道估计方法NMSE对比

由图7中1D-CNN与其他信道估计方法归一化均方误差（normalized MSE，NMSE）对比曲线。发现1D-CNN在整个信噪比区间内其NMSE更低。其中在SNR<15，时1D-CNN信道估计方法的NMSE值远远低于LMMSE方法与LS方法。分析得出LS算法性能最差，LMMSE算法由于其充分利用信道信息，方实现信道估计，但是由于在算法实施过程中并不能及时利用时延采样点求取观察矩阵，该算法的复杂度决定了其应用范围。1D-CNN算法NMSE性能优秀的原因在于，通过对信道信息做标签之后再对神经网络进行迭代，使得算法在离线阶段便能训练完成。

6  结束语

提出的基于深度学习的OFDM系统下的信道估计，通过一维卷积神经网络进行数据训练，网络训练在信道估计的离线阶段大大降低了信道估计的算法复杂度。在仿真实验过程中，与传统的LS算法以及LMMSE算法相比较得出，基于深度学习的OFDM系统下的信道估计在在误比特率性能以及归一化均方误差方面都表现更优。

参考文献：

[1]  Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain.[J]. Psychological Review, 1958, 65(6):386-408.

[2]  周飞燕,金林鹏,董军. 卷积神经网络研究综述[J].计算机学报,2017,40(06):1229-1251.

[3]  Adaptive subgradient methods for online learning and stochastic optimization. Duchi, John,Hazan, Elad,Singer, Yoram. Journal of Machine Learning Research . 2011.

[4]  朱锡祥,刘凤山,张超,吕钊,吴小培.基于一维卷积神经网络的车载语音识别研究[J].微电子学与计算机,2017,34(11):21-25.

[5]  Bjarne Grimstad,Henrik Andersson. ReLU networks as surrogate models in mixed-integer linear programs[J]. Computers and Chemical Engineering,2019,131.

[6]  J. Ma and L. Ping, “Data-aided channel estimation in large antenna systems,” IEEE Trans. Signal Process., vol. 62, no. 12, pp. 3111–3124,Jun. 2014.

[7]  单智群. 空间调制中的信道估计与信道跟踪算法研究[D].哈尔滨工业大学,2019.

[8]  肖霖. MIMO-FBMC系统导频辅助信道估计技术研究[D].东南大学,2017.

作者简介：

孙玉霖(1995— ) 男 工学硕士 齐鲁工业大学（山东省科学院） 研究方向：物联网工程