关键词：傅立叶变换FFT；滑动DFT；MATLAB；PSIM；FPGA

1  引言

有限长序列离散傅里叶变换(DFT)和快速傅里叶变换(FFT)是数字信号频谱分析的基本算法。在某些信号处理的应用领域，特别是在一些电力电子应用中，频域中分析离散信号有更加直观，高效。分析电力系统各个时刻其输入样本对应的频谱，可以通过一段时间的窗口来完成时域到频域的样本采集和计算。

对于传统的FFT算法来说，对于某一时刻，用FFT计算出其所有频谱，如果要计算下一时刻的频谱，则再进行一次FFT运算，这两次FFT运算是孤立进行的。而实际上，对于连续的两个时刻，我们会发现，其窗口中的样本有着很大的相似性，后一个时刻的样本只是将前一个时刻的样本的第一个输入舍弃，而在最后添加一个新的样本。滑动DFT算法正是基于这样的思想而进行的探讨，对于两个连续时刻的频谱，已知前一时刻频谱，则可以通过简单的递推运算，得到后一时刻的频谱，这在连续的实时谱分析中有着重要的实际意义。

递归的滑动DFT算法和FFT比起来，FFT算法只能毫无选择的计算出全部的离散频谱，适合全景频谱分析，而递归的滑动DFT算法可以计算某单个离散频谱，具有选择性计算特定次频谱的优点。FFT算法一般要求输入序列长度是N的2的整数次幂。而递归算法的输入序列长度N可以选取任意正整数，并且N的调整不会引起递归单元硬件的改变。FFT算法需要将N个输入序列全部采集完成并整理成数据桢后，在利用碟形结构进行DFT谱计算，数据处理时间至少包含N个数据的采集时间和数据转换时间，而对于滑动DFT算法，更适合同时采集数据和处理数据，非常有利于数据处理的实时性^[1]。

2  滑动DFT的设计（算法介绍）

对于一个离散时间信号，其DFT变换为：

由于全部为实数运算，硬件实现结构简单，计算量少^[3]。

当对连续的不同时刻的信号进行N点谱分析，FFT算法对于每个时刻，都要产生Nlog2N次复乘运算，例如计算10个时刻的信号谱则需要10Nlog2N次复乘运算。而滑动DFT算法，只要知道了前一时刻的信号谱下面每一时刻的复乘运算量仅为N次，连续M个时刻的信号谱的复乘运算量则为MN次，这与FFT算法中M个时刻的信号谱需要MNlog2N次复乘运算量相比，当N取值较大时，计算量降低了许多。如N=1024，则降低了10倍。

3 实现方法（FPGA实验）

以前对滑动递归算法的使用多是以单个模块为运算模块，只适合谱值较少的应用场和。随着技术的发展，现在现场可编程门阵列（Field Program Gata array，FPGA）存储资源越来越大，里面含有大量的乘法器，加法器和DSP类IP核。递归单元所需硬件资源少，且相对固定，不受工作参数变化等影响，巧妙的运用了FPGA强大的并行处理能力，来计算频谱。在目标函数中引入时延约束和锁相处理，提出了简化的迭代设计计算。同时在FPGA上采用多路并行乘法，多级流水加法链等设计，减少FPGA实现所需的时钟周期数，降低计算时延。

通过电网周期倍数点波形数据的更新，波形序列x(n)与窗序列h(n)的逐点相乘，分成每段N点长的波形采样序列，并将对应点相加以及循环移位。波形序列的乘法运算中，各个序列值之间是时序上相互独立的，即允许各序列的乘积运算并行进行。根据这一特性，设计“RAM乘法运算器”形式的基本单元，将数据乘窗操作分解为N 路并行乘法以得到加权序列Xn(m)，使乘法运算时间缩短为原来的1/N。为进一步提高处理速度，将序列里叠加运算设计成M级流水加法链，使单点的叠加求值速度提升M倍。此外，通过写入地址的循环更迭控制来实现对所求取序列Un(q)的循环移位操作，也避免了使用移位寄存器带来的额外处理时延^[6]。

4  仿真验证

首先采用PSIM与Modelsim联合仿真，对DFT模块进行验证。基于文件数据方式，首先在PSIM中生成n次谐波数据，并存入文件harmonic_wave.txt。然后在 Modelsim中，导人数据形成激励信号，驱动DFT模块仿真．仿真过程中实时获取DFT结果。用Modelsim仿真的内容包括：频率1000Hz（10次）谐波输入，采样频率为20000Hz，每电网周期400点。采样时域信号生成离散序列，从中选取100点作为样本，进行DFT变换。旋转因子乘法运算尾数舍入采用四舍五入法。首先给出10次PSIM的序列点波形图如图1所示。对该序列作N=400点的傅里叶变换，得到傅里叶变换的频谱如图2所示。

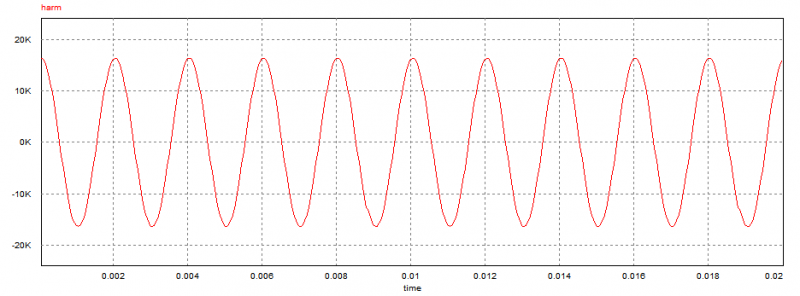
图1  10次谐波波形图

Fig 1  Tenth harmonic waveform

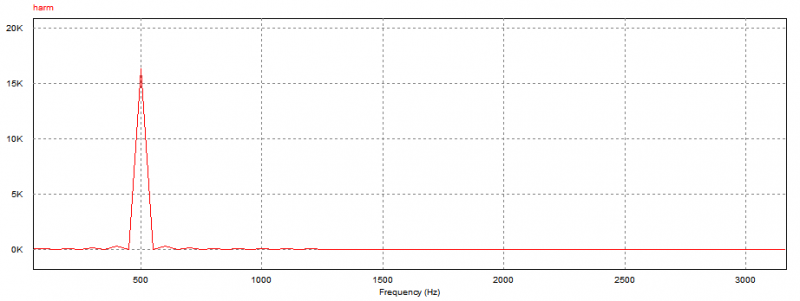
图2  10次谐波频谱图

Fig 2 Tenth harmonic spectrum

根据DFT算法将计算DFT变换电路分为乘累加器、平方器、加法器、开方器.采用LPM模块组合为DFT处理器。其中，Sin-D[15...0]和Cos-D[15...0]分别表示为正弦波形和余弦波形的16位数据(带符号)，在初始化的时候分别写入相应的存储器中。Xn[15...0]表示通过A/D电路采样后的波形数据,也存储在相应的存储器中^[4]。

对连续信号采样取点数N太小必会使DFT精度下降，导致分辨率不够，发生频谱泄漏，严重时还会引起栅栏效应，但如果采样点数过大，必然会占用大量系统资源而且影响系统的测量速度。根据FPGA资源大小，系统的采样点数选取为400点。整个采样数据的存储和计算由FPGA状态机控制，开始计算前先采集400点当前采样率采集得到的数据，并存入400字节的RAM，采集完成后，开始计算，此时保持采样数据不变，通过相应的采样数据和表中的Sin_D和Cos_D，送到DFT处理器入口；每计算一个DFT值，采样得到数据需依次取出并送入运算100次，而Sin_D、Cos_D表中的数据需要以地址累加值递增的形式取出并送入运算100次，地址累加值从0开始，每计算一次DFT加1，得到的DFT结果依次存到后级的16位RAM中。通过乘累加器(MULT-ADD)计算，然后将其值代入平方器(MUL)和加法器(ADD)后得到X² (k)，最后通过开方器完成对以上结果的开方，得到相应的X(k)，最终实现了DFT变换。DFT结果的存储采用再内建FPGA内部的16位双口RAM，可方便地使刷新数据和显示读出数据同时进行，而不产生逻辑冲突，同时也保留了结果的精度^[5]。将该序列数据，通过modelsim进行DFT变换。锁相环及A相数据如图3所示。结果10次的波形，结果（6395^2+(-229)^2）开方后乘以2.56得到16382，结果正确。1-50次DFT结果如图4所示。

图3  锁相环及A相数据

Fig 3  Phase-locked loop and phase A data

图4  1-50次DFT结果

Fig4  1-50 DFT results

5  实验结果

为验证本文提出的锁相环性能，搭建了实验平台。平台采用Analog Devices公司的ADSP21489和INTEL公司(FPGA)EP4CE40F23I7作为核心控制器，三相四线制电网信号源通过模拟信号采集转化成低压信号传入CPU板，包括三相电压、三相电流负载侧、三相电流电网侧等等。在CPU板上，信号通过AD芯片输入至FPGA中，DSP和FPGA配合完成电网锁相处理后，进行DFT运算。给出一个quartus的RTL形成框图。离散傅里叶变换RTL图如图5所示。

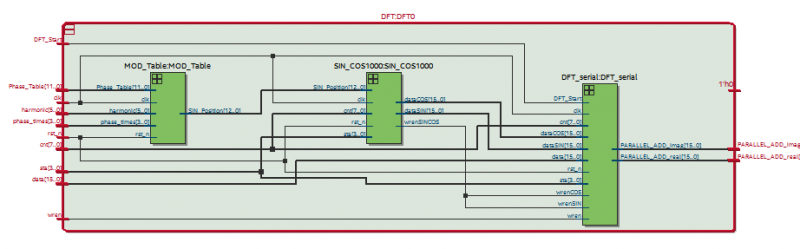
图5  离散傅里叶变换RTL图

Fig 5  Discrete Fourier Transform RTL

用两台APF做验证，其中一台APF向电网中注入三次谐波，另外一台进行闭环检测验证。示波器抓的波形，上位机抓的波形。用示波器捕获电网中的补偿前负载电流波形和补偿后网侧的电流波形。如下：

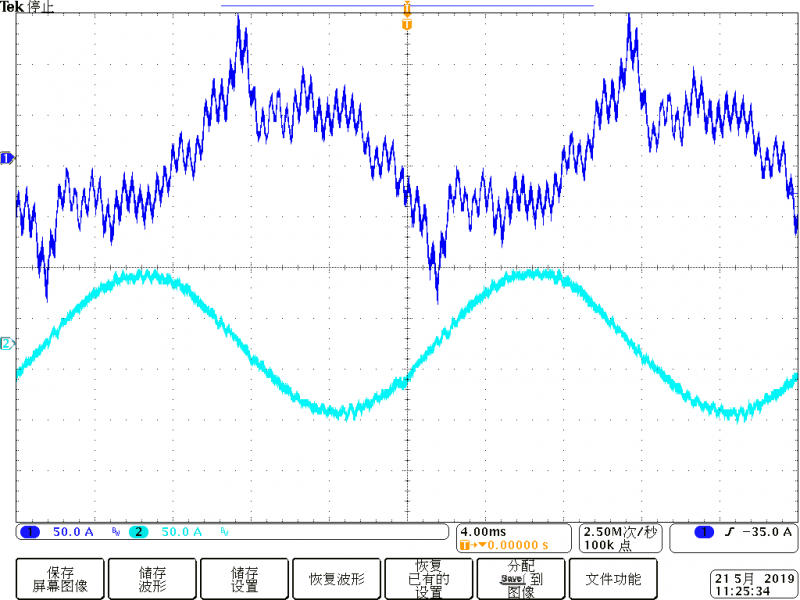
图6  谐波检测低通滤波器仿真模型

Fig 6  harmonic detection simulation model of the low-pass filter

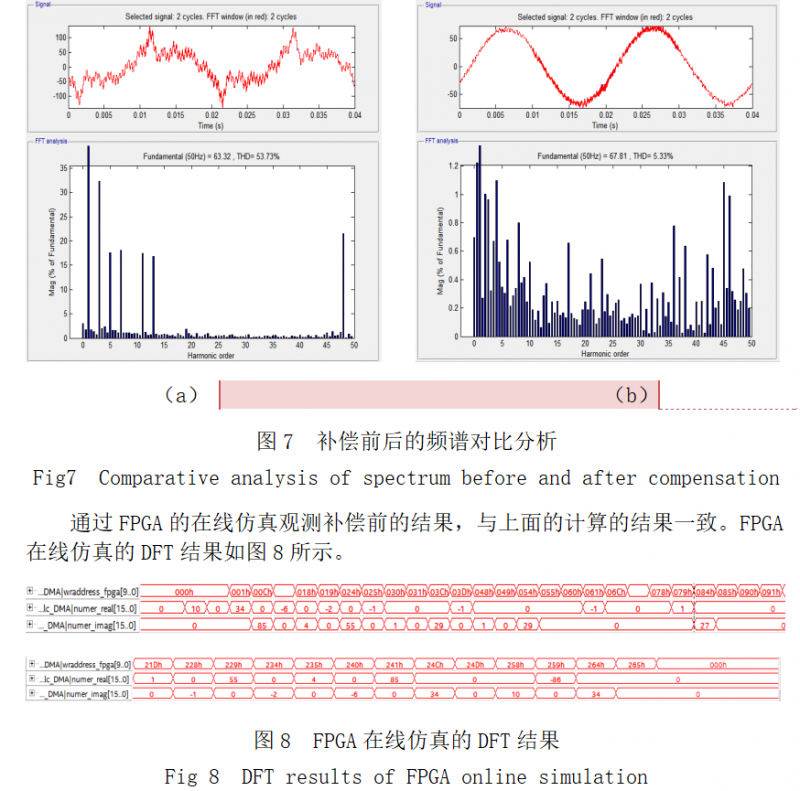
图中蓝色部分为APF设备负载侧的电流波形，里面含有3，5，7，11，13，48次谐波，浅蓝色为经过DFT分析后的，补偿后的波形，谐波大部分已经被处理掉了。首先通过Matlab 的powergui的FFT分析得出补偿前和补偿后的对比图，补偿前后的频谱对比分析如图7所示。

在仿真时，为了验证算法设计的正确性和可行性，仿真采用了时序仿真。仿真结果示于图8。从图中可以看出，3次谐波的值为(sqrt(55^2+(-1)^2))*0.64=35.2058，5次和7次谐波的值为(sqrt(29^2+(-1)^2))*0.64=18.5710，11次谐波的值为(sqrt(27^2+(0)^2))*0.64=17.2800。48次谐波的值(sqrt(34^2+(0)^2))*0.64= 21.7600，与用MATLAB仿真得出的结果相符。证明设计是正确的。实际项目的设备中补偿3-49次谐波，设备一直稳定运行状态良好。

6  结束语

理论分析和仿真实验表明，采用FPGA实现DFT计算，FPGA所具有的并行特性使其在实 时性要求高或者计算复杂度大的研究中得到比DSP更为广泛的应用。

逐点滑动DFT算法频率单元的数据输入率与数据输出率相同，可以实时处理数据。FFT算法虽然能以较快的速度计算出全部N点离散频谱，但其N点快速傅里叶变换（FFT）的数据处理时间至少包括N个时域样本的采集时间和时域数据向频域数据转换的计算时间。而对于逐点滑动DFT算法，采集一个时域数据，输入到频率单元后，经过几次算术运算，便可以输出一个频域数据。如果在一个采样间隔时间内，能完成这固定且有限的几次算术运算，便可以做到边采样、边计算、边输出，从而实现了实时处理。

本文在谐波数据仿真的基础上，通过FPGA上优化DFT算法，采用多路并行乘法，多级流水加法链等设计，减少FPGA实现所需的时钟周期数，减少计算时延。测试表明，电力电子有源滤波器系统中，在80K采样的吞吐率需求下，并行实现20K的构DFT运算在谐波综合处理的取得明显效果。本方法及构建的语音分析和综合系统适用于实时电力电子应用领域。

参考文献：

[1] 王兆安,杨君,刘进军. 谐波抑制和无功功率补偿[M]. 北京:机械工业出版社,1998:257-327.

[2] 王宏伟. 滑动离散傅里叶算法输出稳定性研究[J]. 电波科学学报,2010,29(1):773-779.

[3] 陈勇,姚新宇,潘玉林,唐小凤. 雷达实时仿真中的动目标检测技术研究[J]. 微电子学与计算机,2012,29(6):81-86.

[4] 王宏伟,郑文秀. 计算DFT谱的改进递归算法[J]. 系统工程与电技术,2013,35(9):2263-2268.

[5] 王颖. 宽带雷达数字接收机数据处理方法研究[D]. 江苏科技大学，2012.

[6] 薛一鸣,陈鹞,何宁宁,胡彩娥,王建平. 基于DFT滤波器组的低时延FPGA语音处理实现研究[J]. 电子学报. 2018,46(3):695-701.、
[7] 刘华吾,孙永恒,胡海兵,邢岩. 谐波畸变电网下的单相同步旋转坐标系锁相环[J]. 电力系统自动化. 2016,40(13):93-99.

[8] 葛玉敏. 电力系统谐波、无功和负序电流检测方法的研究[D]. 长春:长春理工大学,2005.

 作者简介：赵爽（1984-），男，辽宁鞍山人