基于PLC的PSO算法PID输送机速度控制技术研究

发布日期：2021-05-31 来源：《变频器世界》21-01期作者：张忠雨浏览次数：12736

分享到：

【摘　要】：本文主要利用粒子群优化算法（PSO）确定输送机系统速度控制中的最佳PID控制器增益。该项目通过三菱Q系列UDV PLC实现，该PLC带有多个编码器传感器和一个内置以太网模块来监控反馈。为了验证该方法的性能，将PSO离线确定的最优增益应用于模拟器和实际模型。实验结果表明，与其它方法相比，所提出的基于粒子群算法的PID控制器具有较低的暂态波动和较小的稳态误差。

关键词：输送机系统；粒子群优化算法；PLC

Abstract: This work focuses on use of particle swarm optimization (PSO) to identify the optimal PID controller gains in speed control of a conveyor system. A proposed method is implemented on Mitsubishi Q series-UDV PLC with a number of encoder sensors and a built-in Ethernet module to monitor the feedback. To verify the performance of the proposed technique, we apply the optimal gains, which are determined offline by PSO, to the simulator and actual model. The experimental results show that the proposed PSO based PID controller provides lower transient fluctuation and smaller steady-state error compared to other previous approaches.

Key words: Conveyor system; PSO; PLC

1 项目介绍

PLC已被广泛应用于工业自动化的大部分领域，采用了一系列数字和模拟逻辑功能来控制适当的输出，例如电机的速度、运行方式等。在大多数由鼠笼式感应电机驱动的输送系统中，由于转子阻力随运行工况变化，速度控制任务具有较高的非线性和大量的参数，具有一定的挑战性。一般情况下，典型的传送带速度控制通过PLC闭环控制系统中PID控制器来实现。然而，目前PID控制器中最难解决的问题之一是如何确定合适的PID增益，而优化算法使用不当可能导致解决方案不理想。

本文介绍了一种利用粒子群算法（PSO）对典型PLC控制的工业输送系统进行PID整定的新方法。将粒子群算法应用于PID中，确定控制器的增益Kp、Ki和Kd。这些最佳增益可以直接分配给指令，然后在PLC模块内部处理。所提出的基于PSO的输送机系统PID可以通过PLC功能进行少量修改而提供接近最佳的性能。从仿真和实际系统测试的实验结果来看，与其他传统方法相比，该种方法在瞬态和稳态区域都提供了较为满意的响应^[4]。

2 输送系统结构

本项目输送系统如图1所示，拖动系统采用感应电机实现，由于电机的速度依赖于输入电压，可以通过调节0～10V的输入电压来控制输送带的运动。使皮带旋转的感应电动机与一组编码传感器一起工作如图2所示，该传感器安装在皮带上，以感测运动中容器的速度和位置。本项目建立的输送系统的结构是由一个六个组装站的平台支

3 控制器设计

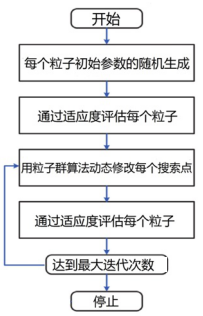
图4 PSO优化流程图

PSO的解给出了公式（5）中性能指标函数的最小值。根据图4使用粒子群优化算法求解的步骤如下：

（1）得到了输送系统的数学模型。

（2）初始化代表控制器增益的30个随机粒子，并将“迭代大小”设置为100。

（3）选择状态和控制权矩阵Q和R。

（4）使用Simulink计算性能指标值。

（5）设置每个粒子的局部最佳值Pbest，并确定总体的全局最佳值Gbest。

（6）通过比较适应度函数来更新全局最优值，并检查终止条件的迭代次数。如果满足终止条件，转到步骤8，否则继续步骤7。

（7）更新粒子速度v和位置x，循环到步骤4。

（8）得到最优增益矩阵K，即最后更新的Gbest。

4 结果分析

首先应用粒子群优化算法得到PID的最优增益矩阵K。在PSO问题中，随机生成30个PID增益矩阵作为初始粒子。通过（2）-（4）迭代搜索最优增益矩阵的解，直到任何迭代的最佳粒子稳定或达到最大迭代。然后，通过PLC指令，将基于PSO算法的最优增益解分配给实际的输送机系统。最后将此方法与其他方法的结果进行了比较，如图5所示。

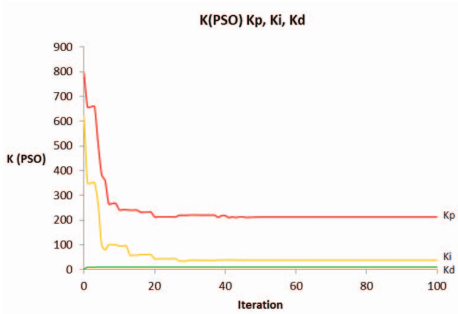
图5 从PSO得到的PID增益

图5显示了每次迭代的PID增益的最佳解决方案。从图5中可以看出，由于第一次随机生成，搜索开始时的最佳解与最终值相差甚远。但随着迭代次数的增加，偏差急剧减小。对于迭代规模为100和群体规模为30，代表实验传送系统的最佳PID增益的全局最佳组分如表1所示。

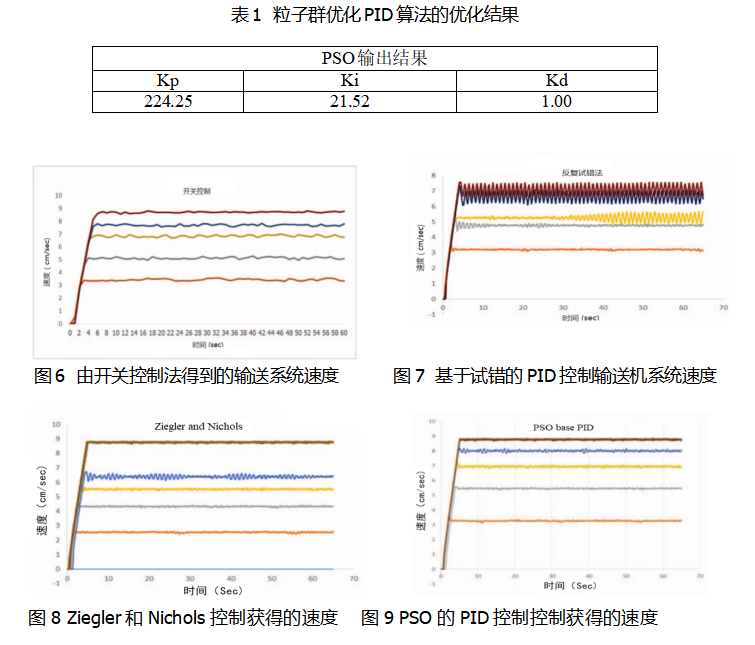
图6-图9分别显示了四种不同方法的输送机速度结果：开关控制、基于试错的PID控制、Ziegler和Nichols控制以及提出的基于PSO的PID控制。在整个实验过程中，电机的目标速度水平设定为额定速度的30%（3.25cm/s）、60%（5.5cm/s）、75%（7.0cm/s）、85%（8.0cm/s）和100（8.75cm/s）。为了便于比较，本项目还选择了一些不同方法的初始增益，使得它们的瞬态响应类似有界[3]。

图6绘制了开-关方法的电机速度，该方法的最大值和最小值之间的最大误差为0.35 cm/s，稳态误差最大为15.38%。尽管在此研究中使用的小型电动机使整个响应平稳且快速，但是对大型系统来说提供了较慢的响应，因此开/关控制可能不是最佳的选择。于前一种方法相比图7中基于试错的PID产生的速度提供了极大的振荡，该方法最大摆幅与最低摆幅的最大差值为0.8cm/s，最大稳态误差为11.43%。对于如图8所示的Ziegler和Nichols方法，摆幅和稳态误差低于前两种方法，最大峰间振荡为0.3cm/s，稳态误差为6.67%。在图9中可以看到，提出的基于PSO的PID方法的结果优于其它，具有相对较低振荡的算法，其最大峰值差约为0.2cm/s，最坏情况下的稳态误差仅为5.25%。

5 结论

本项目提出了一种用于输送机的感应电动机调速的新方法系统。采用PSO算法确定PID增益矩阵并用几种优化方法进行了比较，实验结果表明，基于粒子群算法的PID控制算法是可行的与其他方法相比，该技术具有更好的响应速度，最大峰峰值差仅为0.2cm/s，比基于试错的PID方法低4倍，比on-off和Ziegler & amp; Nichols方法低约1.5倍。