关键词：电抗器；简化模型；icepak仿真；温升

Abstract:In this paper, the single-coil AC reactor is studied. By analyzing the heat dissipation process of the reactor, a simplified model is established, and by analyzing the difference between the simplified model and the equivalent model, the anisotropic equivalent thermal conductivity of the simplified model is determined, and the loss correction method is given. Use icepak to establish a simulation model and build a test platform. The simulation and test results show that the temperature rise range of the model can meet engineering requirements and can provide a reference for the heat dissipation research of reactors.

Keywords: Reactor; Simplified model; Icepak simulation; Temperature rise

 

1  引言

在变频调速系统中，为防止因操作交流进线开关产生的过电压和浪涌电流对变频器的冲击，减小谐波对电网的污染，使之符合相关法规与标准，熟悉与变频器配套用的各类电抗器的作用和容量的选择等问题是有必要的。与变频器相配套用的有交流输入电抗器、直流电抗器、交流输出电抗器、零序电抗器、正弦波滤波器等。由于电抗器的用途较为广泛，许多研究者对电抗器的温升进行了研究，杨建立等人^[1]通过ANSYS建立1/8结构体的详细模型，研究了单个干式空心电抗器绕组的温度分布；张允^[2]采用流体动力学方法，建立三维模型并划分了280万以上网格计算了特高压并联电抗器的的温度分布；方伟^[3]在利用ICEPAK研究低压变频器的热仿真设计时，给出了低压变频器用电抗器的构造图和尺寸图，但并未给出模型建模方法及搭建参数；由上述研究者的研究方法及研究结果可知，目前对于电抗器的仿真研究存在两个问题，一是采用详细建模，在保证网格精度的情况下能得到较为精确的温升值和温度范围，但绝大部分电抗器线圈之间的气隙和线圈本体的尺寸量级相差1~2个数量级，若要保证气隙的网格精度，会导致整个模型的网格数量很大，一方面对计算机的配置要求很高，另一方面也限制了该方法在系统建模仿真的应用；另一个问题是目前尚未有文献针对电抗器的建模方法、参数设定以及仿真和测试对比进行系统的阐述。因此急需一种既能满足电抗器温升及温度范围仿真工程要求，又能控制网格数量且运用到系统中去的工程仿真方法，本文从电抗器的结构出发，分析其传热路径，详细阐述了模型简化搭建过程、相关物理参数计算过程，最后将仿真结果与实验进行对比，为各位工程人员研究电抗器温升以及其温度对于系统中其它元器件的影响提供方法借鉴。

 

2  电抗器简化模型

本文所研究的电抗器实物如图1所示，由线圈和铁芯组成的直流电抗器，整个电抗器的散热途径包括内部导热，外部对流换热和辐射，因辐射在工业产品温升范围内占据的比例较小，尤其是在强迫风冷中可忽略，本文主要从导热和对流换热方面进行等效研究。

 

图1  单层线圈交流电抗器

 

电抗器线圈是绕铁芯的螺旋状，因每层线圈的上升角比较小，因此原电抗器模型可等效成如图2所示的由一层层方线圈和连接条组成，其中该等效等效模型涉及到的参数有：

线圈导热系数λ₁，w/m k；

空气导热系数λ₂，w/m k；

线圈宽W，m；

线圈高H，m；

线圈与铁芯上下间距M，m；

线圈与铁芯左右间距N，m；

线圈截面高b，m；

线圈截面宽a，m；

空气隙l，m；

A₁：线圈的横截面积，m²；

A₂：空气隙的横截面积，m²。

   

 

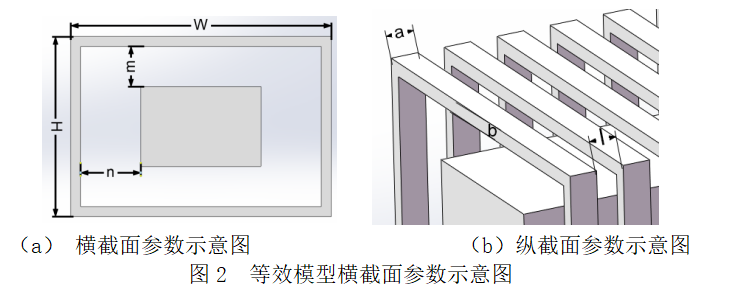
每层方线圈可以看做是由上、下、左、右四个直线圈组成，方线圈参与对流换热的面积是直线圈对流换热面积的总和，每个直线圈的对流换热面积包括如图3所示的4个面，其计算公式为：

上、下直线圈的换热面积计算为：

S-out=a*W                     （1）

S-in=a*（W-2*b）              （2）

S-side=b*W                    （3）

左、右直线圈的换热面积计算为：

S-out=a*(H+2*b)                （4）

S-in =a*（W-2*b）             （5）

S-side=b*H                    （6）

 

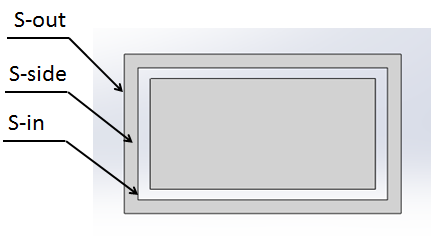
图3  直线圈对流换热面示意图

电抗器实际安装位置会导致上述每一个面的对流换热系数有所不同。计算整体对流换热量时，应分别计算出每个面的对流换热量后进行叠加。

如图4所示是是本文所讨论的单层电抗器的简化模型，除线圈总长度不同以外，其它尺寸同方线圈，其中线圈总长为L。

 

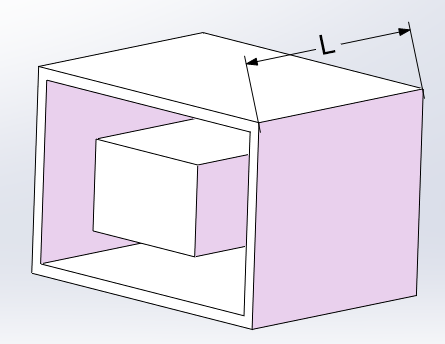
图4  电抗器单个绕组的简化模型

3  简化模型参数计算

由上述模型简化过程可知，简化模型等效性主要关注两部分，一部分是平均温升，由公式可知，该部分温升主要由对流换热面积和对流换热系数决定，涉及损耗修正；另一部分是温度分布，该部分由模型三维导热决定的，涉及各方向等效导热系数计算。因此实现对简化模型的散热等效性研究主要包括对流换热特性和等效导热系数两部分。

3.1  对流换热特性

如表1所示是本次研究的电抗器实体模型的参数表。

 

                                                                                                      

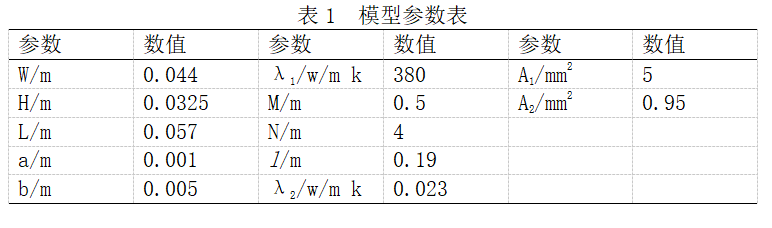
备注：表2是44匝线圈总的面积

 

 

                                                                                                 

 

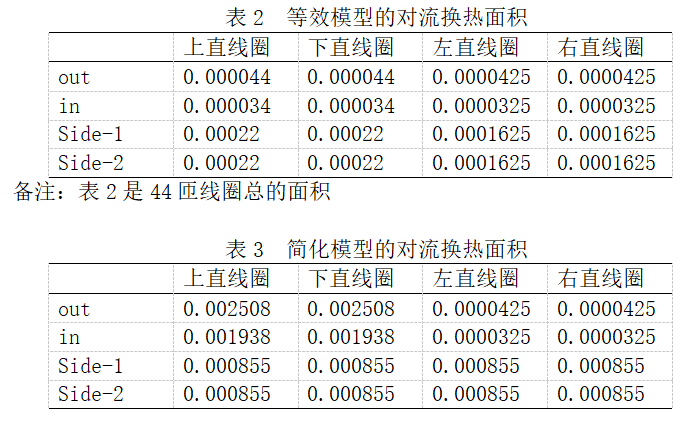
因方线圈各个方位的对流换热工况不同，其对流换热系数也不一致，利用对流换热特征数方程、自然散热水平热面和竖直热面Nu数方程、强迫对流Nu数方程和电抗器实际安装位置进行换热系数的相对大小和数量级估算，分别评估各直线圈不同方位的对流换热系数，如表4和表5所示。

 

                                                                                         

 

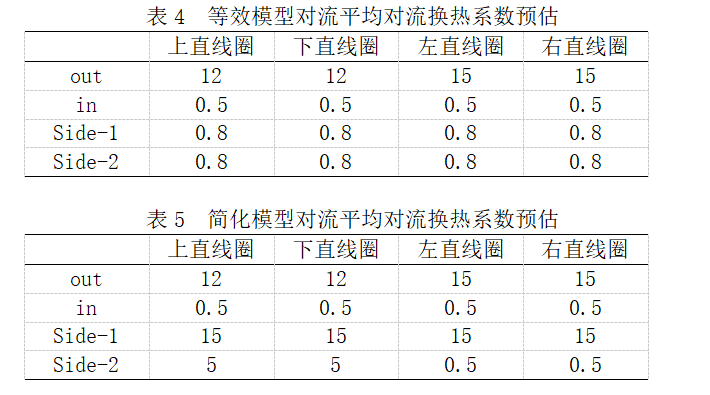
依据表A~表B计算自然散热时等效模型和简化模型的HA分别为0.163W/K和0.132W/K，由P=HAΔT，若要保证平均温升相同，则P/HA要相等，根据该原则对等效模型的损耗进行修正，因此等效模型线圈损耗为22W经过修正后得到简化模型的损耗值为17.8W。

依据表A~表B计算强迫风冷时等效模型和简化模型的HA分别为0.283W/K和0.2W/K，由P=HAΔT，若要保证平均温升相同，则P/HA要相等，根据该原则对等效模型的损耗进行修正，因此等效模型线圈损耗为22W经过修正后得到简化模型的损耗值为15.5W。

3.2  各项异性导热系数推算

因实际线圈的横截面如图5所示，可以看做是由图5所示的“线圈+空气隙”单元组成，对该单元进行横向和纵向导热分析。

 

图5  线圈和空气隙单元

3.3  纵向等效导热系数推算

纵向等效导热系数可以看做是线圈的空气的在截面的并联，根据热阻等效原理，推算模型的等效导热系数^[4]。

空气的一维导热热阻为：

Rth2=δ/（λ₂×A₂）              (7)

线圈的一维导热热阻为：

Rth1=δ/（λ₁×A₁）            (8)

因此等效一维热阻为：

λ-co1=（λ₁×A₁+λ₂×A₂）/（A₁+A₂）        (9)

代入表1中的参数，计算结果为319W/m k。

3.4  横向等效导热系数

横向等效导热系数的确定有两种，一种是类似于纵向导热系数的推算方法一样，计算铜线圈热阻与空气隙热阻的串联，其中铜线圈热阻计算如下：

Rth-cu=a/(λ₁×W×b)             （10）

空气隙的热阻是由对流换热热阻和导热热阻的并联^[5]，其计算公式为

Rth-air=(1/Rth-w+1/Rth-X)^-1              （11）

式（11）中：Rth-w为导热热阻；Rth-X为对流换热热阻。

因此横向的导热热阻为：

Rth-横=Rth-cu+Rth-air           （12）

理论上而言，利用公式（12），带入相应的参数即可求出横向的等效导热系数，但必须要指出的是因对流换热的强弱不同，其边界层厚度不同，且对流换热的定义里本身就包含了导热作用，因此在利用上述计算公式时，难以判定对流换热与导热的界限，即实际判定Rth-air时有一定的难度。但以单个等效模型中的一匝方线圈为分析对象，计算其毕涡数^[4]小于0.05时的对流换热系数：

h≤0.05×λ1/（2×（W+H））=0.05×380/（2×（0.044×0.0325））=124W/m² k

因此在该对流换热系数以内，横向和纵向的散热量比在很小范围内波动，对温升结果无本质影响，从该角度出发，以空气隙为纯空气导热为计算工况，算得横向等效导热系数为0.14。

3.5  连接条等效导热系数

在上述计算横向和纵向的等效导热系数时，是仅从横向和纵向截面进行分析的，而实际的线圈是螺旋形的，因此除了上述的横向和纵向导热以外，等效模型还应包括每匝线圈之间因线圈的热传导，根据导热热阻等效原理，在简化模型中，建立连接条来模拟该部分热传导，并根据热阻等效计算该连接条的相关参数：

λ-co3×a×b=λ1×a×b×l/W                  (13)

带入表1中的数据得连接条的等效导热系数λ-co3为1.6W/m k。

 

4  测试与仿真对比

将上述计算结果带入仿真模型中，并搭建实验进行验证。

4.1  自然散热

图6为搭建的测试平台，图7为根据测试平台搭建的仿真模型，图8为测试布点示意图，测试结果见表6。

     

 

 

  

比较上述测试和仿真结果可知，测试结果和仿真结果均表明，线圈中心温度最高并向两边递减，线圈最高温升预测较好，均为67.6℃；测试线圈的温升范围为58.7℃~67.6℃，仿真线圈的温升范围为61℃~67.6℃，最大温升误差为4%。

4.2  强迫风冷

图10为搭建的强迫风冷测试平台，图11为根据测试平台搭建的仿真模型，布点位置同自然散热，测试结果见表7。

   

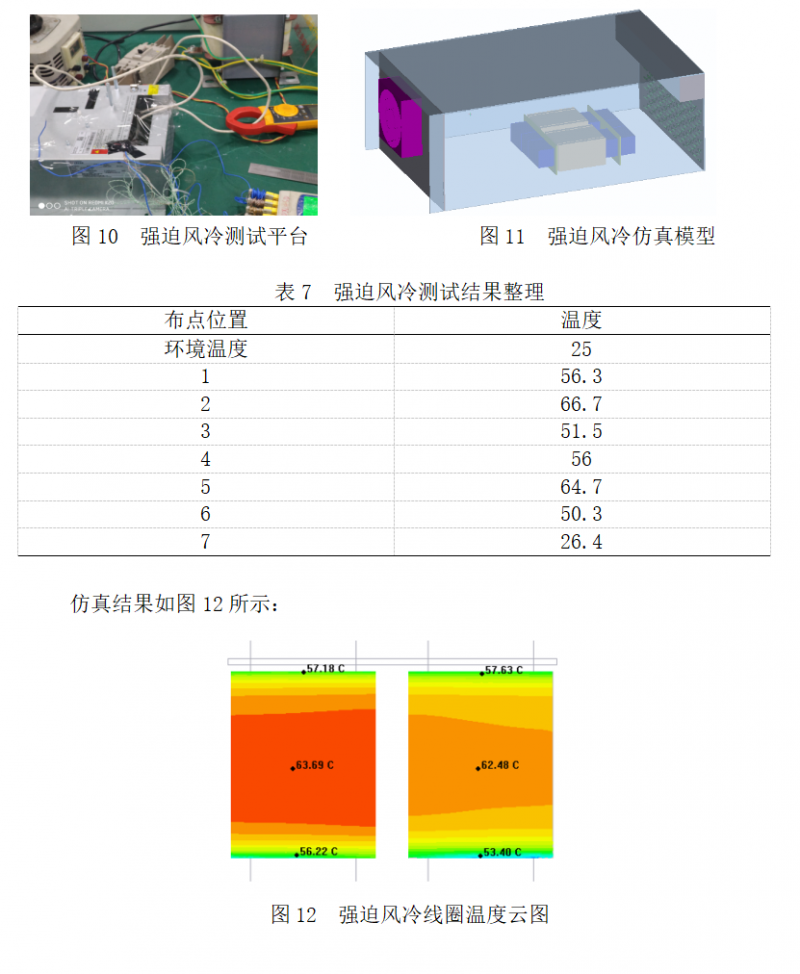
比较上述测试和仿真结果可知，测试线圈最大温升为41.7℃，仿真最大温升38.7℃，测试线圈的温升范围为25.3℃~41.7℃，仿真线圈的温升范围为28.4℃~38.7℃，温升误差范围为7.2%~12.3%。

 

5  总结

本文通过分析电抗器的散热过程，建立简化模型并进行icepak仿真和实物测试，对比仿真和测试结果表明，自然散热和强迫风冷仿真的最高温度和实测均较为接近，全温升范围的误差在15%以内，可满足工程精度要求。

值得指出的是，电抗器在设计、制造及使用的过程中，材料，尺寸、加工工艺、使用工况等均有不同，因此本文并未直接给出电抗器等效导热系数的唯一值，而是详细分析了计算过程中各个参数的确定方法，并通过实验和仿真验证了该方法的有效应，以供各位工程师参考从而应对不同的实际使用工况。诚然，对流换热系数的估算需要了解产品结构以及使用场合，其数值精准度与工程师的经验有关，但工程师仍可通过分析对流换热经验公式，借助仿真与实测得到相关数值。

 

参考文献：

[1]杨建立, 徐政勋, 聂京凯,等. 干式空心电抗器温升仿真技术研究[J]. 电力电容器与无功补偿, 2019(6).

[2]张允. 单心柱特高压并联电抗器温度场研究[D]. 山东大学，2017.

[3]方伟. 基于热仿真的低压变频器的设计及研究[D]. 苏州大学，2016.

[4]杨世铭, 陶文铨. 传热学（第4版）[M]. 高等教育出版社, 2006.

[5]庞旭明, 周剑秋, 杨晶歆,等. 含孔隙及界面热阻的复合材料有效导热系数[J]. 中国有色金属学报, 2016, 026(008):1668-1674.

 

作者简介：

郭盼盼（1993 年-）女，硕士，热设计工程师，就职于上海辛格林纳新时达电机有限公司 研究方向为变频器散热设计。