关键词：表贴式永磁同步电机；矢量控制；转子位置估计；高频方波电压注入

Abstract: Permanent magnet synchronous motor (PMSM) has the advantages of high efficiency, high power factor and high power density, which is widely used in the field of electrical drives. In terms of the problem of poor rotor position estimation accuracy in sensorless control technology for traditional rotating high frequency voltage injection method and pulsation high frequency voltage injection method in surface mounted permanent magnet synchronous motor (SPMSM) speed regulation system at zero speed and low speed, a sensorless control technology of SPMSM based on high frequency square wave voltage injection method is proposed based on the analysis of rotor saliency of surface mounted permanent magnet synchronous motor. The simulation results show that the proposed method can overcome the shortcomings of the above two traditional sensorless control techniques, and has the advantages of high accuracy of rotor position estimation and good dynamic performance of speed regulation.

Key words: Surface mounted permanent magnet synchronous motor (SPMSM); Vector control; Rotor position estimation; High frequency square wave voltage injection

1  引言

永磁同步电机（PMSM）具有非常好的力能指标，广泛地应用于电力传动领域。根据转子永磁体安装方式，PMSM可分为表贴式永磁同步电机（SPMSM）和内置式永磁同步电机（IPMSM），二者在工作原理和调速性能上具有不同的特点。SPMSM因具有结构简单、成本低廉的优点，广泛应用于变频家电和交流伺服等场合。为降低成本和提高调速性能，PMSM无传感器转子位置辨识问题得到了广泛的研究和应用。为进一步提高SPMSM的调速性能，需要解决零速和低速下传统的高频电压注入无传感器矢量控制方法存在估计精度差的问题^[1-2]。PMSM转子位置和速度估算方法主要有：（1）基于基波数学模型的PMSM无传感器矢量控制方法，包括滑模观测器法、模型参考自适应法、扩展卡尔曼滤波法^[3-5]，这些方法通过PMSM的反电动势进行转子位置和速度估算，依赖于反电动势检测，由于PMSM低速运行时反电动势幅值较低，提取困难，所以这种方法通常适用于电机中高速运行场合；（2）基于高频信号注入的无传感器矢量控制方法，包括旋转高频电压信号注入和脉振高频电压信号注入^[5]，其基本思想是通过检测高频信号在电机中产生的响应来估计转子的位置^[6-10]。旋转高频电压信号注入是一种最常用的高频注入，需要在PMSM定子电压上叠加一个三相平衡的高频正弦电压信号，根据高频激励下的PMSM数学模型，对于凸极电机，注入旋转高频信号，产生的电流响应负序分量中包含了转子位置信息。因此，通过合适的滤波和计算即可观测出转子位置和速度。这种方法依赖于电机的凸极性，仅适用于IPMSM无传感器矢量控制，不适用于SPMSM，且该方法需要使用多种滤波器，计算复杂，存在较大的相位滞后，因而调速动态效果较差^[11-18]。文献[19]针对滤波器造成的相位延迟提出了一种补偿算法，利用相位影响因素对正序和负序电流分量产生相位延迟具有的相关性，通过提取正序电流分量中的相位偏差，对负序电流分量的相位进行补偿，一定程度上提高了转子位置估计精度。脉振高频电压信号注入是在估计的PMSM同步旋转d-q坐标系中的d轴上注入高频正弦电压，根据PMSM高频激励下的数学模型，该注入信号在估计同步旋转d-q坐标系q轴上的响应中包含有估计同步旋转d-q坐标系和真实同步旋转d-q坐标系的误差角，即转子估计位置误差角，通过适当的观测器如锁相环即可使转子估计位置误差角收敛到零，从而估计出准确的转子位置和速度。该方法同样依赖于电机的凸极性，也需要使用多种滤波器，调速动态效果较差，但不同的是这种注入方法可以使隐极式永磁电机产生饱和凸极性，所以该方法也可以用于SPMSM^[20-25]。

通过以上分析可知，基于高频信号注入转子位置辨识的矢量控制能够实现良好的控制效果，但各类滤波器的使用造成了严重的相位滞后，影响了系统的调速控制性能。此外，高频注入法转子位置辨识依赖于电机d-q轴电感的差异，即电机的凸极性，基于旋转高频正弦电压注入法的转子位置辨识只适用于凸极性明显的IPMSM，而基于脉振正弦高频电压注入的转子位置辨识可以改变d轴的饱和凸极性而适用于SPMSM。对于SPMSM调速系统，为了进一步改善零速和低速下传统高频电压注入的无传感器矢量控制方法存在转子位置估计精度差进而影响调速性能的问题，提出了基于高频方波注入法的SPMSM无传感器矢量控制方法，采用理论分析、仿真模拟展开研究，期望能够改善旋转高频信号注入和脉振高频电压信号注入的无传感器矢量控制方法的不足，以此提高转子位置估计精度和改善调速动态性能。
4  高频方波注入法SPMSM转子位置辨识

2.1  转子位置辨识原理

PMSM定子电压方程为

  

通常注入PMSM的高频信号频率大于0.5kHz，对应的角频率远高于电机的基波电角频率ω_e，因此可以忽略基波角频率相关项的影响，将PMSM视为RL串联电路，又由于高频激励下定子电感L_s的感抗远大于定子电阻的阻值，因此可以忽略定子电阻R_s的影响，高频信号注入下的永磁同步电机电压方程可简化为

            （2）

式中，u_dh为定子电压d轴高频分量；u_qh为定子电压q轴高频分量；i_dh为定子电流d轴高频分量；i_qh为定子电流q轴高频分量。

与脉振高频正弦注入法相似，高频方波注入法是在估计的两相旋转坐标系中注入高频方波信号，坐标关系如图1所示，注入的高频信号可表示为

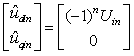           （3）

图1 高频方波信号注入示意
 

由式（13）可知，转子位置估计误差与旋转坐标q轴电流的导数成正比，可以参考脉振高频正弦注入思路进行转子位置观测器构造来获得准确的转子位置，但是在实际应用中，进行检测电流求导存在困难，同时需要对电流进行滤波，不仅造成相位的滞后，控制系统内外部的干扰也会影响转子位置估计的精度，控制系统的鲁棒性较差，因此需要提出一种新的信号提取处理方式。

2.3 无滤波器信号提取方法

采用高频信号注入转子位置辨识方法时，需要将电机定子电流中的高频响应分量分离提取出来。传统高频信号注入方法需要使用滤波器，包括低通滤波器和带通滤波器，滤波过程中必然导致相位滞后，缩小控制系统的带宽，影响控制效果。同时，滤波器的设计与数字实现比较困难，大量数字滤波算法也会过渡开销数字控制器的运算资源。采用高频方波注入的一个突出优点就是信号提取过程可以不采用滤波器，而仅采用容易的代数运算。

高频方波注入信号的波形与估计在旋转坐标系q轴电流响应波形及时序关系如图2所示，注入方波信号的频率远高于电机供电基波频率，周期为T_s，电流采样频率固定为注入方波信号频率的2倍，且设置采样点如图2虚线所示。

图2  注入信号和电流响应波形

由于注入信号的频率远高于电机供电基波频率，首先假设q轴电流的基波分量在相邻两个采样周期内保持恒定，则可认为的变化完全是由方波输入信号引起的，因此根据图2可得q轴基波电流分量为

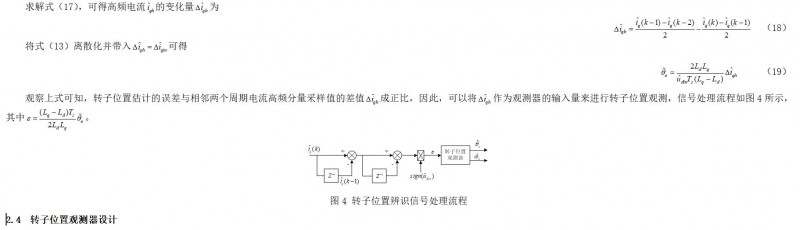
传统的转子位置辨识通常采用基于PI调节器的观测器，控制结构如图5所示，其核心是采用PI调节器构成锁相环（PLL）系统。

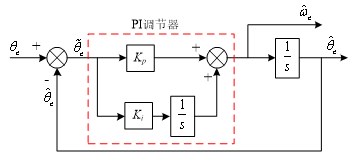
图5 基于PI调节器的转子位置观测器结构

根据图5，可写出其闭环传递函数为

     （20）

由式（20）可知，这是一个二阶系统，分析可以发现传统基于PI调节器的PLL观测器在设计时将转子位置和转速两个变量作为系统状态变量进行考虑，但是在实际电机系统中，首先由电流的变化引起转矩的变化，再由转矩的变化引起转速和转子位置的变化。传统基于PI调节器的PLL观测器往往存在响应速度慢的问题，因此，如果在设计转子位置观测器时能够将转矩考虑在内，可以提高系统的响应速度，加快观测器的收敛速度。

将电磁转矩与转子位置、转速共同考虑为状态变量，参考自抗扰控制中的扩张状态观测器（ESO）原理^[26-28]，可以设计一个基于ESO理论的转子位置观测器。由于电机控制系统的控制周期远高于机械时间常数，设计观测器时可以将电机负载转矩看作不变量，可得状态方程为

       （21）

式中，T_e为电磁转矩；T_L为负载转矩；K₁、K₂、K₃为待整定参数。

对上式左右两边同时积分，可得

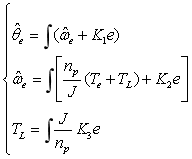     （22）

根据式（4-20）可得转子位置扩张状态观测器如图6所示。

图6 转子位置扩张状态观测器结构

根据上图，可推导出转子位置扩张状态观测器的闭环传递函数为

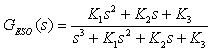  （23）

根据线性扩张状态观测器理论，参数K₁、K₂、K₃可以通过极点配置法来确定，将三个极点配置在负实轴上-ρ点处，即特征方程配置为(s+ρ)³，此时系统具有良好的稳定性和动态性能，因此可以得出相应参数为

     （24）

同理，式（20）中传统PI观测器参数可配置为

         （25）

不失一般性，选择ρ=10，分别绘制传统PI观测器系统和ESO系统的闭环波特图，如图7所示。从图中可知，ESO带宽明显高于传统PI观测器，这说明了ESO具有更好的频率特性和更快的响应速度。

图7 传统PI观测器系统和ESO系统的波特图

综上所述，建立基于高频方波信号注入的表贴式永磁同步电机无传感器矢量控制系统，如图8所示。与传统高频电压信号注入法进行对比，高频方波注入使用简单的数学计算代替了滤波器进行信号处理，并且使用ESO代替了传统PI观测器，为验证该控制系统的性能，需要进行进一步仿真分析。

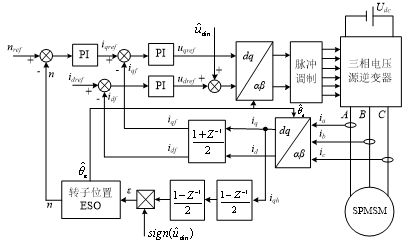
图8 基于高频方波注入SPMSM无传感器矢量控制系统

3 高频方波注入法SPMSM转子位置辨识仿真分析

为验证高频方波注入法SPMSM无传感器矢量控制性能，在MATLAB/Simulink仿真环境中搭建图8所示的仿真模型，仿真参数设置如表1所示。

                                                             

仿真中注入高频方波信号的幅值为20V，频率为5kHz，控制系统的采样频率为10kHz。首先对采用PI转子位置观测器的高频信号注入无传感器矢量控制系统进行仿真，选择给定转速n_ref分别为100r/min和1000r/min进行仿真，初始负载转矩均为5N∙m，在0.5s时，负载转矩阶跃至10N∙m。

图9为给定转速100 r/min时定子电流波形，其中图9（a）为d-q轴电流，图9（b）和图9（c）分别为采用无滤波器提取方法提取的q轴基波电流和q轴高频电流，图9（d）为采用带通滤波器滤波器提取的q轴高频电流。从图中可知，无滤波器提取方案可以有效地从d-q轴电流分离出基波分量和高频分量，对比图9（c）和图9（d）可以发现相比传统滤波器提取方案，无滤波器提取方案的高频信号提取分离效果具有更明显，有利于转子位置辨识。

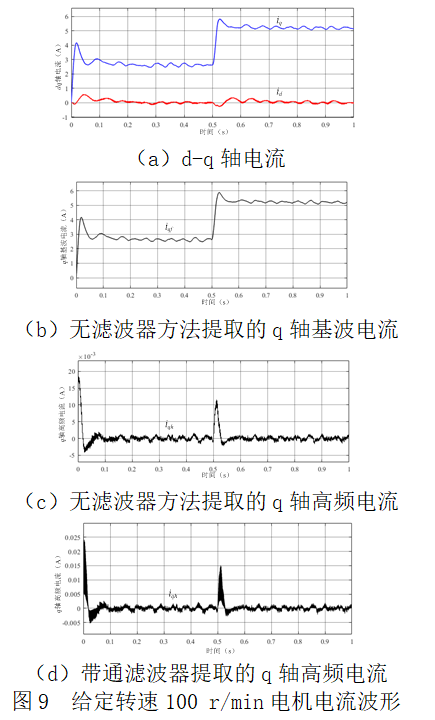
图10与图11为分别是给定转速100 r/min和1000 r/min时电机转子位置与转速波形，图10（a）、（b）、（c）与图11（a）、（b）、（c）依次为实际转子位置和估计转子位置波形、转子位置估计误差波形、实际转速和估计转速波形。从图中可知，基于高频方波电压注入的转子位置估计方法能够实现转子位置的准确辨识，能够实现有效的SPMSM无传感器矢量控制。在给定转速100 r/min运行进入稳态后，转子位置估计误差小于0.01 rad，转速估计误差小于10 r/min。在系统给定转速1000 r/min运行进入稳态后，转子位置估计误差约为0.01 rad，转速估计误差小于10 r/min，转子位置和转速估计精度都远高于现有两种传统高频电压信号注入法，且在不同给定转速下的系统性能差距明显减小。这说明无滤波器高频电流提取方法的应用提升了系统的带宽。系统给定转速100 r/min在负载阶跃时，电机转速跌落50 r/min后在0.2 s内恢复，转子位置辨识误差仍小于0.02 rad，系统给定转速1000 r/min在负载阶跃时，电机转速跌落50 r/min后在0.1 s内恢复，转子位置辨识误差小于0.05 rad，证明矢量控制系统具有较强的抗扰动能力和良好的动态性能。

为验证转子位置扩张状态观测器的性能，对基于ESO的高频注入无传感器矢量控制系统进行仿真分析，并与基于PI观测器的高频信号注入无传感器矢量控制系统进行对比，主要对比负载变化时两种观测器跟踪效果。电机初始负载转矩设置为10 N∙m，0.4 s时阶跃上升至15 N∙m，0.7 s时阶跃下降回10 N∙m。

图12为给定转速1000 r/min时基于ESO的无传感器矢量控制系统的电机转子位置、转速波形，图12（a）、（b）分别为实际转子位置和估计转子位置波形、实际转速和估计转速波形。图13为给定转速1000 r/min时ESO和传统PI观测器转子位置估计误差对比。图14为给定转速1000 r/min时ESO和传统PI观测器转速估计误差对比。

从以上各图可知，两种观测器的稳态误差基本相等，但动态过程存在显著差别。采用传统PI观测器时，电机启动后转子位置误差和转速误差收敛至稳定值所需时间分别为0.33 s和0.25 s，负载阶跃上升后转子位置误差和转速误差收敛所需时间分别为0.17 s和0.1 s，负载阶跃下降后转子位置误差收敛和转速误差所需时间分别为0.15 s和0.11 s。采用ESO时，电机启动后转子位置误差和转速误差收敛至稳定值所需时间分别为0.12 s和0.13 s，负载阶跃上升后转子位置误差和转速误差收敛所需时间分别为0.04 s和0.05 s，负载阶跃下降后转子位置误差和转速误差收敛所需时间分别为0.08 s和0.04 s。通过对比可以发现，ESO的转子位置误差收敛和转速误差收敛时间都明显短于传统PI观测器，证明了ESO具有更高的带宽、更快的动态响应和更优秀的动态特性。

5  结论

对于在零速和低速下运行的PMSM传统系统，基于基波数学模型的无传感器矢量控制方法由于依赖于反电动势检测而不适用，旋转高频电压信号注入法由于依赖于电机转子磁路的凸极性而仅适用于IPMSM无传感器矢量控制，脉振高频电压信号注入法可使隐极式电机产生饱和凸极性可以适用于SPMSM无传感器矢量控制，但是该方法与旋转高频电压信号注入法一样都需要使用多种滤波器，因而存在转子位置与转速估计信号相位滞后问题，影响了动态调速效果。提出了一种基于高频方波注入法的SPMSM无传感器矢量控制方法，无需使用滤波器，仅仅采用代数计算方法，不存在转子位置与转速估计信号相位滞后问题。在分析转子位置提取方法和无滤波器信号提取方法后，针对传统转子位置观测器响应速度较慢问题，设计了转子位置扩张状态观测器，然后完成基于MATLAB/Simulink的仿真分析。结果表明，该改进后的高频方波注入SPMSM无传感器矢量控制策略具有转子位置估计精度较高以及动态调速性能较好的优点。

参考文献：

[1] 袁登科，徐延东，李秀涛. 永磁同步电动机变频调速系统及其控制[M]. 北京：机械工业出版社，2015年6月.

[2] 袁雷，胡冰新，魏克银，陈姝. 现代永磁同步电机控制原理及MATLAB仿真. 北京：北京航空航天大学出版社，2016年4月.

[3] 李永东, 朱昊. 永磁同步电机无速度传感器控制综述[J].电气传动,2009,39(09):3-10.

[4] 谷善茂, 何凤有, 谭国俊, 叶生文. 永磁同步电动机无传感器矢量控制方法现状与发展[J].电工技术学报, 2009,  24(11):14-20.

[5] 孙凯翔. 永磁同步电机无传感器矢量控制及参数辨识研究[D].合肥工业大学, 2019.

[6] X. Luo, Q. Tang, A. Shen and Q. Zhang. PMSM sensorless control by injecting HF pulsating carrier signal into estimated fixed-frequency rotating reference frame[J]. IEEE Transactions on Industrial Electronics, 2016 ,63(04):2294-2303.

[7] M. Seilmeier and B. Piepenbreier. Sensorless control of PMSM for the whole speed range using two-degree-of-freedom current control and HF test current injection for low-speed range[J]. IEEE Transactions on Power Electronics, 2015, 30(08): 4394-4403.

[8] Q. Tang, A. Shen, X. Luo and J. Xu. PMSM sensorless control by injecting HF pulsating carrier signal into ABC frame[J]. IEEE Transactions on Power Electronics, 2017,32(05): 3767-3776.

[9] G. Feng, C. Lai, K. L. V. Iyer and N. C. Kar. Improved high-frequency voltage injection based permanent magnet temperature estimation for PMSM condition monitoring for EV applications[J]. IEEE Transactions on Vehicular Technology, 2018,67(01): 216-225.

[10] E. de M. Fernandes, A. C. Oliveira, C. B. Jacobina and A. M. N. Lima. Comparison of HF signal injection methods for sensorless control of PM synchronous motors[J]. 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, 2010: 1984-1989.

[11] 于艳君,柴凤,欧景,高宏伟. 基于旋转高频信号法的IPMSM无位置传感器控制[J]. 电工技术学报, 2013, 28(07): 26-31.

[12] 李浩源, 张兴, 杨淑英, 杨健, 李俊. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(08): 1723-1731.

[13] 李华阳, 王涛, 林环城, 龚黎明, 陈金涛, 诸自强. 基于高频注入的PMSM无传感器矢量控制的误差分析[J]. 微特电机, 2013, 41(11):64-70.

[14] A. H. Almarhoon, Z. Q. Zhu and P. Xu. Improved rotor position estimation accuracy by rotating carrier signal injection utilizing zero-sequence carrier voltage for dual three-phase PMSM[J]. IEEE Transactions on Industrial Electronics, 2017, 64(06): 4454-4462.

[15] W. Sun, J. Shen, M. Jin and H. Hao. A robust magnetic polarity self-sensing method for start up of PM synchronous machine in fanlike system[J]. IEEE Transactions on Industry Applications, 2017,53(03):2169-2177.

[16] M. Rashed, P. F. A. MacConnell, A. F. Stronach and P. Acarnley. Sensorless indirect-rotor-field-orientation speed control of a permanent-magnet synchronous motor with stator-resistance estimation[J]. IEEE Transactions on Industrial Electronics, 2007 ,54(03):1664-1675.

[17] J. M. Liu and Z. Q. Zhu. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame[J]. IEEE Transactions on Industry Applications, 2014,50(04):2574-2583.

[18] 吴春. 永磁同步电机调速系统无位置传感器控制技术研究[D]. 西北工业大学, 2016.

[19] 杨健, 杨淑英, 李浩源, 张兴. 基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法[J].电工技术学报, 2018, 33(15):3547-3555.

[20] 刘颖, 周波, 冯瑛, 赵承亮. 基于脉振高频电流注入SPMSM低速无位置传感器控制[J]. 电工技术学报, 2012,27(07):139-145.

[21] A. H. Almarhoon, Z. Q. Zhu and P. L. Xu. Improved pulsating signal injection using zero-sequence carrier voltage for sensorless control of dual three-phase PMSM[J]. IEEE Transactions on Energy Conversion, 2017,32(02): 436-446.

[22] A. Accetta, M. Cirrincione, M. Pucci and G. Vitale. Sensorless control of PMSM fractional horsepower drives by signal injection and neural adaptive-band filtering[J]. IEEE Transactions on Industrial Electronics, 2012, 5(03):1355-1366.

[23] P. L. Xu and Z. Q. Zhu. Carrier signal injection-based sensorless control for permanent-magnet synchronous machine drives considering machine parameter asymmetry[J]. IEEE Transactions on Industrial Electronics, 2016,63(05): 2813-2824.

[24] P. L. Xu and Z. Q. Zhu. Comparison of carrier signal injection methods for sensorless control of PMSM drives[C]. 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, 2015:5616-5623.

[25] J. Lara and A. Chandra. Performance investigation of two novel HSFSI demodulation algorithms for encoderless FOC of PMSMs intended for EV propulsion[J]. IEEE Transactions on Industrial Electronics, 2018, 65(02): 1074-1083.

[26] W. Xue, W. Bai, S. Yang, K. Song, Y. Huang and H. Xie. ADRC with adaptive extended state observer and its application to air–fuel ratio control in gasoline engines[J]. IEEE Transactions on Industrial Electronics, 2015,62(09):5847-5857.

[27] J. Huang, P. Ma, G. Bao, F. Gao and X. Shi. Research on position servo system based on fractional-order extended state observer[J]. IEEE Access, 2020,8:102748-102756.

[28] H. Sira-Ramírez, J. Linares-Flores, C. García-Rodríguez and M. A. Contreras-Ordaz. On the control of the permanent magnet synchronous motor: an active disturbance rejection control approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22 (05):2056-2063.