叶思文1 沈一鹤1 朱佳伟1 魏铭欧1 杨喜军1 江剑峰2 陈圣泽2
1上海交通大学电气工程学院,上海,200240 2国网上海市电力公司营销服务中心,上海,200051
摘要:基于实际电感电流与期望电感电流的斜率关系,分析了单相功率因数校正器(PFC)中升压电感过零交越失真机理,给出了几种能够提高网侧过零附近升压电感端电压的电路,使得实际电感电流上升斜率明显大于期望电感电流,无需改变原有控制结构和控制策略。分析了采用三相-两相平衡变压器(Scott变压器)以及单相功率因数校正器来实现三相AC-DC变换器的原理,并探讨了在航空供电频率应用的可能性。
关键词:电感电流过零交越失真,三相-两相平衡变压器;三相AC-DC变换器;单相功率因数校正器
Analysis of Three-phase AC-DC Converter Using Three-phase/Two-phase Balanced Transformer
YE Siwen1 SHEN Yihe1 ZHU Jiawei1 WEI Mingou1 YANG Xijun1 JIANG Jianfeng2 CHEN Shengze2
1. Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240
2. Marketing Service Center, State Grid Shanghai Electric Power Company, Shanghai 200051
Abstract: Based on the slope relationship between the actual inductor current and the expected inductor current, the zero crossing crossover distortion mechanism of the boost inductor in a single-phase power factor corrector (PFC) is analyzed. Several circuits are proposed to improve the terminal voltage of the boost inductor near the zero crossing of the grid voltage, so that the actual inductor current slope is significantly greater than that of the expected inductor current without changing the original control structure and control strategy. Then the principle is analyzed using a three-phase/two-phase balanced transformer (eg Scott Transformer) and a single-phase power factor corrector to implement a three-phase AC-DC converter, as well as the possibility of its application with aviation power supply frequency.
Keywords: Inductor current zero crossing cross distortion, three-phase/two-phase balanced transformer; three phase AC-DC converter; single-phase power factor corrector
1 引言
单相功率因数校正器包括功率开关置于桥后、桥中和桥前等多种电路拓扑,可以采用相同或相似的控制结构和控制策略。单相功率因数校正器具有两个受控目标,即直流输出电压和电感电流波形,网侧电流各次谐波电流有效值应该符合相关标准规定的限值[1-5]。实际情况是,无论采取何种调制算法和控制策略,在网压过零附近,电感电流波形都会出现交越失真,随着输出功率增加和电源频率增加,过零畸变愈发严重,影响区间也越大。电感电流过零交越失真机理需要进一步研究。电气化铁路的发展促进了三相-两相平衡变压器技术的进步,例如Scott变压器和LeBlanc变压器,输入三相对称平衡电压,输出两路相位差90°电压。如果三相-两相平衡变压器两组输出绕组连接功率相等的单相功率因数校正器,则可以在其输入侧即网侧获得单位功率因数。考虑到电力变压器体积与供电频率成反比,因此对于航空频率电源而言,可以探索采用成熟的三相-两相平衡变压器和单相功率因数校正器构成三相AC-DC变换器,具有研发周期短和高可靠性优势。本文针对电感电流过零交越失真机理与改进措施、基于三相-两相平衡变压器和单相功率因数校正器的三相AC-DC整流器展开探讨。
2 电感电流过零交越失真原理分析
传统功率开关置于桥后型单相PFC拓扑如图1所示,其功率电路由二极管整流桥和Boost DC-DC变换器前后级联构成,图中采用了单周期控制(OCC)策略。理论上升压电感可以置于桥前,也可以置于桥后。
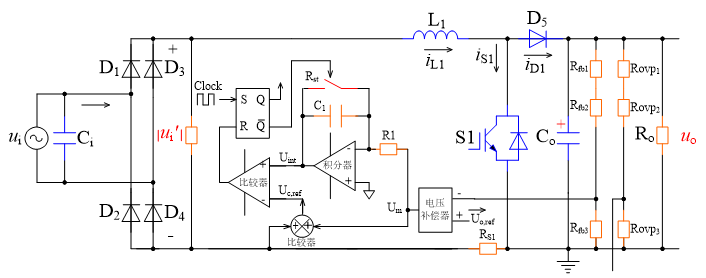
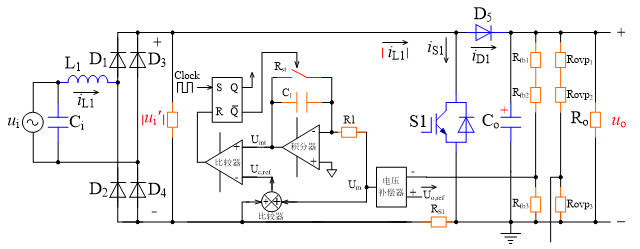
(b) 升压电感置于桥前
图1 单相功率因数校正器拓扑
设单相正弦交流输入电压![]() 为
为
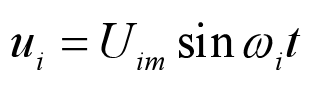 (1)
(1)
式中,![]() 为输入电压幅值;
为输入电压幅值;![]()
![]() 为输入电压角频率。
为输入电压角频率。
假设图1(a)所示的单相PFC已经进入稳态,输出功率已经稳定,网侧呈现单位功率因数,并假定网侧交流电容滤除全部电感纹波电流,则作为双闭环控制结果的参考输入电流![]() 及其导数
及其导数![]() 分别为
分别为
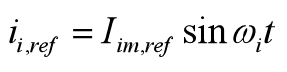 (2)
(2)
 (3)
(3)
式中,![]() 为参考输入电流幅值。
为参考输入电流幅值。
升压电感电流为
 (4)
(4)
式中,![]() 为升压电感电流的纹波分量。
为升压电感电流的纹波分量。
升压电感电流波形如图2所示。根据图2,如果期望实际电感电流能够有效跟踪参考电感电流,上升阶段的实际电感电流斜率应该大于参考电感电流斜率,下降阶段的实际电感电流斜率应该小于参考电感电流斜率。
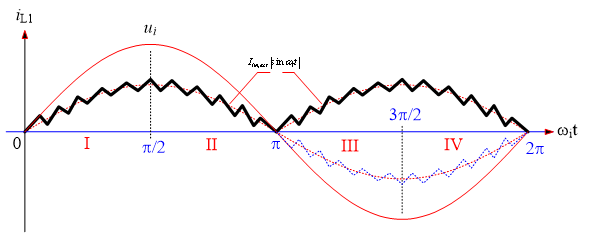
图2 升压电感电流波形
假设,在单相交流电压正半周中电感电流工作在CCM。当功率开关导通时,实际电感电流![]() 上升,此时回路电压方程为
上升,此时回路电压方程为
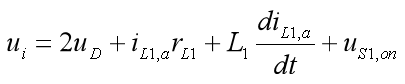 (5)
(5)
式中,![]()
![]() 为单只二极管压降;
为单只二极管压降;![]()
![]() 为升压电感的分布电阻;
为升压电感的分布电阻;![]()
![]() 为升压电感取值;
为升压电感取值;![]() 为单只功率开关的导通压降。
为单只功率开关的导通压降。
进一步可得
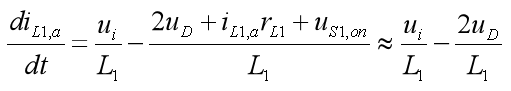 (6)
(6)
式中,![]() 为单只二极管导通压降;
为单只二极管导通压降;![]() 为升压电感分布电阻;
为升压电感分布电阻;![]() 为功率开关导通电阻压降;
为功率开关导通电阻压降;![]() 为升压电感取值。
为升压电感取值。
总体上,![]()
![]() 、
、![]() 起到限制升压电感
起到限制升压电感![]() 电流的上升斜率作用。鉴于它们取值较小,设置
电流的上升斜率作用。鉴于它们取值较小,设置![]() ,并忽略其它项的作用。当功率开关关断时,升压电感电流
,并忽略其它项的作用。当功率开关关断时,升压电感电流![]() 下降,此时电压方程为
下降,此时电压方程为
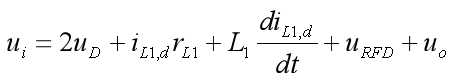 (7)
(7)
式中,![]() 为单只反向恢复二极管的压降。
为单只反向恢复二极管的压降。
进一步可得
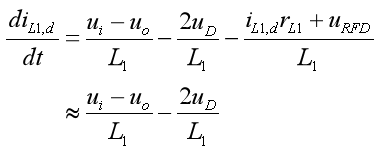 (8)
(8)
总体上,![]() 、
、![]() 与
与![]() 起到加速升压电感
起到加速升压电感![]() 电流的下降作用。鉴于取值较小,设置
电流的下降作用。鉴于取值较小,设置![]() 、忽略其它项的作用。
、忽略其它项的作用。
在区间I中,比较![]() 与
与![]() ,发现二者存在一个交点。设交点处电角度为
,发现二者存在一个交点。设交点处电角度为![]() ,令
,令![]() =
=![]() ,可得
,可得
 (9)
(9)
(1) 当![]() ,电感电流为零,属于盲区,盲区影响范围
,电感电流为零,属于盲区,盲区影响范围![]() 。输入电压有效值越低和二极管压降越大,盲区越大。假设两只二极管与IGBT导通压降之和为2.5V,即
。输入电压有效值越低和二极管压降越大,盲区越大。假设两只二极管与IGBT导通压降之和为2.5V,即![]() 。
。
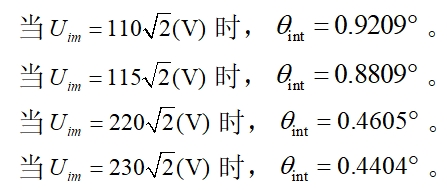
(2) 当![]() ,电感电流不为零。令
,电感电流不为零。令![]() ,可得
,可得![]() 。对于第一项,输入角频率越大和网压幅值越低时,对角度影响越大。对于第二项,网压幅值越低时,对角度影响越大。
。对于第一项,输入角频率越大和网压幅值越低时,对角度影响越大。对于第二项,网压幅值越低时,对角度影响越大。
在网压过零附近,![]() ,
,![]() ,式中,
,式中,![]() 为升压电感的工频感抗;
为升压电感的工频感抗;![]() 为网侧等效电阻。
为网侧等效电阻。![]() 。
。
假设传输效率为98.0%,电源频率为50Hz,升压电感取值250mH,在不同输入电压和频率下对应角度如表1所示。
表1不同输入电压和输入频率下对应角度
|
输出功率(kW) |
输入电压(V) |
输入电流(A) |
对应角度(°) |
||
|
50Hz |
400Hz |
800Hz |
|||
|
3.5 |
115 |
31.05 |
1.2142 |
9.6235 |
18.7328 |
|
220 |
16.23 |
0.3318 |
2.6526 |
5.2938 |
|
|
270 |
13.22 |
0.2202 |
1.7612 |
3.5191 |
|
|
3.0 |
115 |
26.61 |
1.0406 |
8.2680 |
16.2053 |
|
220 |
13.91 |
0.2844 |
2.2738 |
4.5405 |
|
|
270 |
11.33 |
0.1887 |
1.5096 |
3.0170 |
|
可见,随着电源频率、输出功率、升压电感取值的增加,以及随着输入电压有效值降 低,影响区越大。在影响区内,理论上采取各种双闭环控制策略均无能为力,其中包括各种电流过零补偿环。
潜在解决方案为:在网压过零阶段,当功率开关导通时,人为增加升压电感两端电压,以此补偿二极管和功率开关的压降,并使电感电流上升斜率明显大于期望输入电流的上升斜率。具体方法包括:(1)在电感输入端,引入瞬时值足够高的正电压;(2)在电感输出端引入瞬时值足够低的负电压;(3)采用单相四象限PWM整流器代替单相PFC。
对于方法2,当功率开关导通时,可以利用单相PFC输出直流电压,经过DC-DC变换器或DC-AC变换器,在电感输出端引入瞬时值足够低的负电压,如图3、图4和图5所示。
在图3中,功率开关S1和S2同时通断,导通时可以引入负的输出电压,关断时二极管D5和D6提供续流路径,双闭环控制结构保持不变。
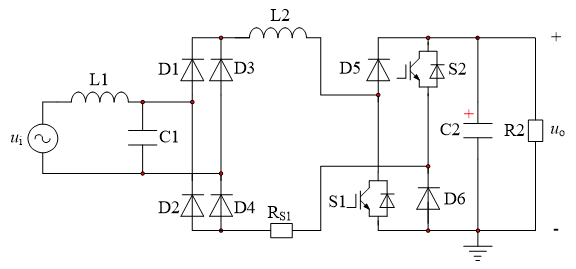
图3 采用DC-AC变换器引入负电压
在图4中,功率开关S3、二极管D7、电感L3和电容C3构成Buck-Boost 变换器,电容C3形成负电压,通过调节功率开关S3占比,负电压幅值可调。当功率开关S1与S2同时通断,导通时可以引入负的直流电压,关断时二极管D5提供续流路径,双闭环控制结构保持不变。
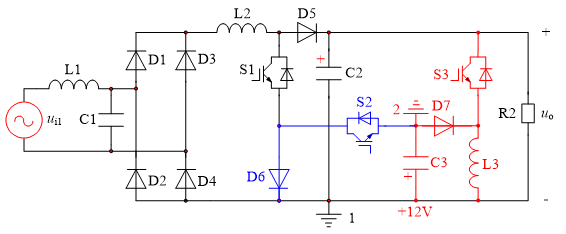
图4 采用Buck-Boost 变换器引入负电压
在图5中,功率开关S3、二极管D7、电感L3与L4、电容C3与C4构成Boost-Buck变换器,即CUK变换器,电容C4形成负电压,通过调节功率开关S3占比,负电压幅值可调。当功率开关S1与S2同时通断,导通时可以引入负的输出电压,关断时二极管D5提供续流路径,双闭环控制结构保持不变。

图5采用Boost-Buck 变换器引入负电压
在区间II中,比较![]() 与
与![]() 大小,发现
大小,发现![]() <
<![]() ,二者均为负数,因此区间II中电感实际电流 波形可以有效跟踪电感参考电流,在理论上完全成立,电感取值越小跟踪越快,大量的仿真和实验结果均可验证该结论。
,二者均为负数,因此区间II中电感实际电流 波形可以有效跟踪电感参考电流,在理论上完全成立,电感取值越小跟踪越快,大量的仿真和实验结果均可验证该结论。
采用MATLAB/Simulink对图1、图3、图4和图5所示PFC电路进行仿真分析,仿真条件为:输入电压为220V。电源频率为50Hz,升压电感取值为1mH,电解电容取值为470mF,开关频率100kHz、负载电阻为28W。均在最佳仿真效果下,可得四种情况下输入电流过零交越失真情况,如图6所示,可见所给出的三种补偿电路具有有效性。
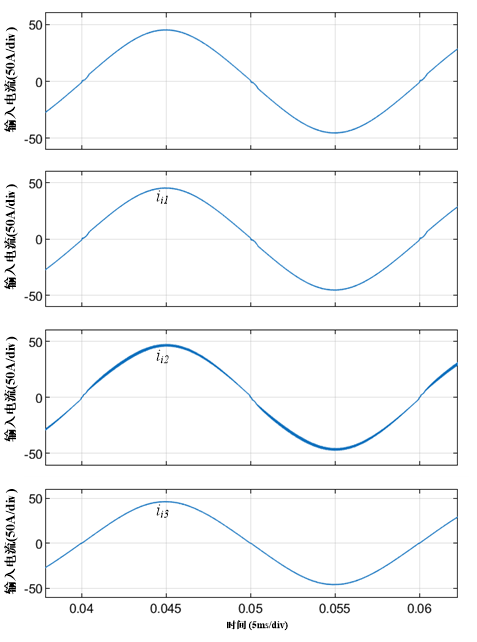
图6 四种情况下输入电流过零交越失真对比
3 基于平衡变压器的三相AC-DC变换器
高速铁路的快速发展带动了电力牵引和平衡变压器的进步,适合电力牵引的接线方式包括:单相、V/V、Y/Δ、YN V D、Scott、Leblanc、Kübler、modified Woodbridge、十字交叉、二次侧中抽式单相、V/X以及二次侧中抽式Scott等。平衡变压器种类很多,包括有源滤波的阻抗匹配平衡变压器十字交叉接线、有源滤波的Scott接线变压器等。重载铁路主要采用自耦变压器(AT)供电,并利用Scott型接线变压器向牵引网供电。Scott接线平衡变压器是最早出现的三相-两相平衡变压器,接线简单,二次侧电气独立,在AT供电方式的牵引系统中,主要用来实现一次侧三相系统与两相牵引供电系统之间的连接。
如图7所示,Scott接线变压器可看作是由两个单相变压器组合构成,可以采用单铁芯结构或双铁芯结构,包括主变压器(Main变压器)和梯变压器(Teaser变压器),梯变压器一次侧绕组端子连接在主变压器一次侧绕组的中点,也可将二次测绕组称作a相与b相。![]() 与
与![]() 幅值相同,频率同一次侧频率,相位差90°,
幅值相同,频率同一次侧频率,相位差90°,![]()
![]() 与一次侧
与一次侧![]() 同相。
同相。
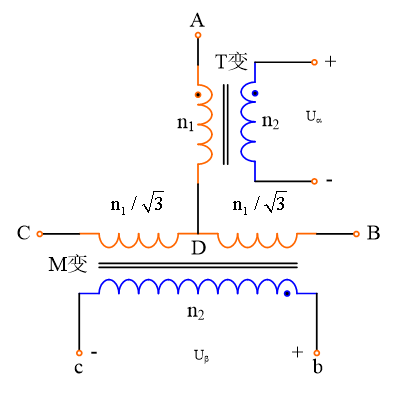
(a)接线关系
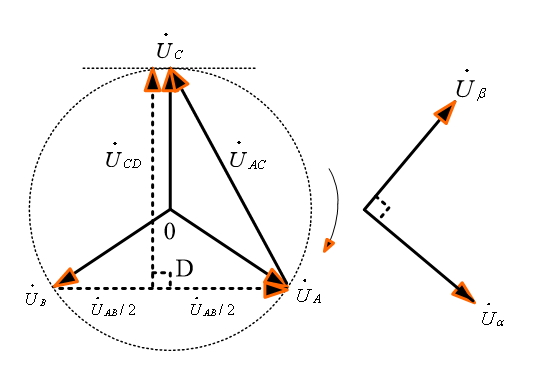
(b)向量关系
图7 Scott 变压器的接线关系与向量关系
三相输入电流与两相输出电流方程为
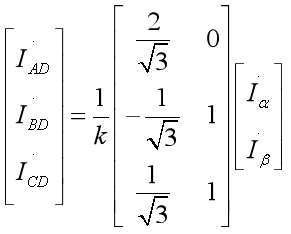 (10)
(10)
两相输入电压与三相输出电压方程为
 (11)
(11)
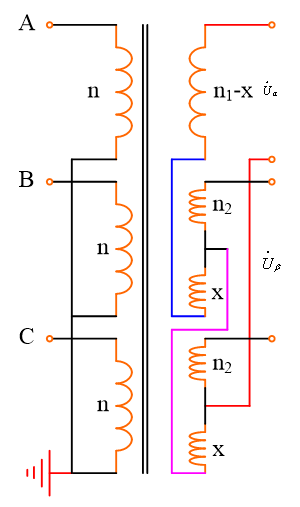
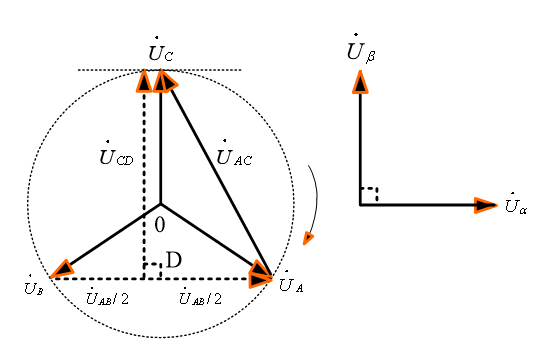
Scott接线变压器的突出优点是:二次侧两相自然解耦,二次侧中点抽出式Scott接线变压器同样具有二次侧两相解耦的特点。此外,互相解耦的变压器还包括modified Woodbridge、二次侧中抽式Scott。Leblanc变压器接线关系和相量关系如图8所示,图中,![]() ,
,![]() 。图9 给出了modified Woodbridge变压器接线关系。Scott变压器其实就是一种具有Clarke变换功能的功率级物理模型,如果Scott变压器次级两相工作在同等功率的单位功率因数下,其初级电源则工作在单位功率因数下,也就是说基于Scott变压器可以用在三相AC-DC变换电路,实现网侧单位功率因数,如图10所示。工频运行的Scott变压器体积较大,变压器的感应电势为
。图9 给出了modified Woodbridge变压器接线关系。Scott变压器其实就是一种具有Clarke变换功能的功率级物理模型,如果Scott变压器次级两相工作在同等功率的单位功率因数下,其初级电源则工作在单位功率因数下,也就是说基于Scott变压器可以用在三相AC-DC变换电路,实现网侧单位功率因数,如图10所示。工频运行的Scott变压器体积较大,变压器的感应电势为![]() ,式中,fi为供电频率;N为绕组匝数;
,式中,fi为供电频率;N为绕组匝数;![]() 为磁路最大主磁通。在相同感应电势下,供电频率越高,主磁通越小,铁芯可以越小,体积相应减少。
为磁路最大主磁通。在相同感应电势下,供电频率越高,主磁通越小,铁芯可以越小,体积相应减少。
(a)接线关系
(b)向量关系
图8 Leblanc变压器的接线关系与向量关系
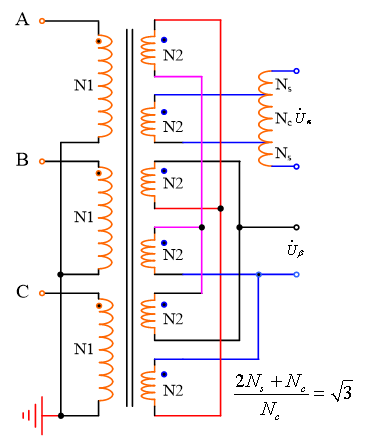
图9 Modified WOODBRIDGE变压器接线关系
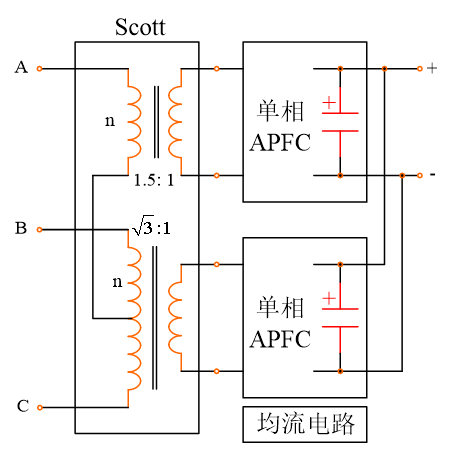
(a)单相PFC输出并联

(b)单相PFC输出串联
图10 采用Scott变压器的三相AC-DC变换电路
鉴于航空电源的工作频率范围为360Hz~400Hz ~800Hz,电压等级为交流115V或230V,Scott变压器体积相比工频50Hz或60Hz,功率体积之比较大,因此可以采用Scott变压器与单相PFC构成高功率因数的三相AC-DC变换电路。在电感电流CCM下,升压电感的取值与开关频率成反比。单相PFC的输出电解电容取值也与电源频率成反比,高频输入有利于降低电解电容体积。当输出侧串联时,输出电压均值加倍,2倍网频的纹波电压对消。当输出侧并联时,输出电压均值不变,2倍网频的纹波电压对消。基于Scott变压器与单相PFC的三相AC-DC变换电路的MATLAB/Simulink仿真电路与主要波形如图11和图12所示,图中,Scott变压器初级为三相电压220V/400Hz,次级为两相电压220/400Hz,单级PFC输出电压期望值为375V,电解电容6x470mF、升压电感250mH,开关频率100kHz、负载电阻为28W,两个单级PFC输出可以设置成独立、串联、并联运行。
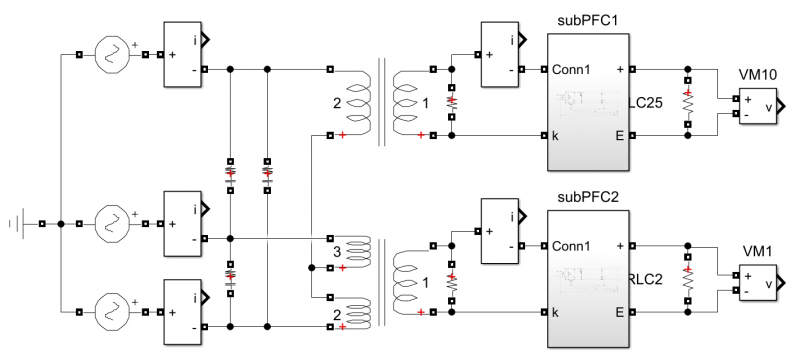
图11三相AC-DC变换电路结构
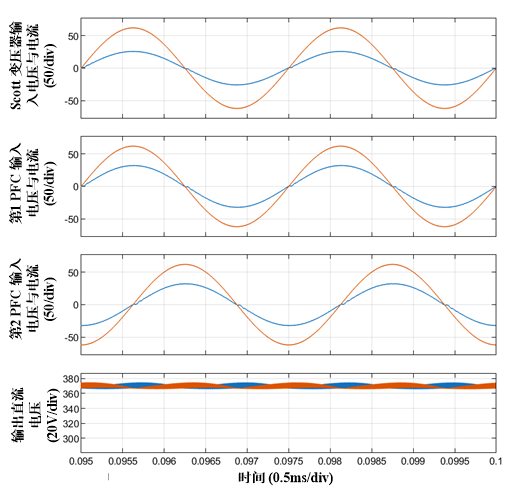
图12 三相AC-DC变换电路主要波形
在单相PFC进入稳态后,二极管电流基波为直流分量与2倍网频电流之和,其中2倍网频电流幅值与直流分量相同。二极管电流直流分量直接刚给负载电阻,二极管电流2倍网频电流几乎全部流入电解电容,形成2倍网频的电容纹波电压。如果电解电容取值足够大,二极管电流的2倍网频纹波电流分量的初相、电解电容的2倍网频纹波电压的初相与网压初相相同,纹波电压峰峰值也较低。如果电解电容取值较小,二者初相将前移,容值越小,前移越明显,纹波电压峰峰值相应增加。图13给出了两组PFC输入电压、输入电流与输出电压波形;图14给出了两组PFC输入电压与二极管电流按开关周期求均值波形。
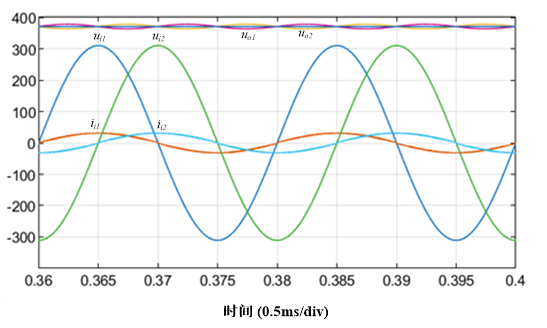
图13 两组PFC的输入电压、输入电流与输出电压波形
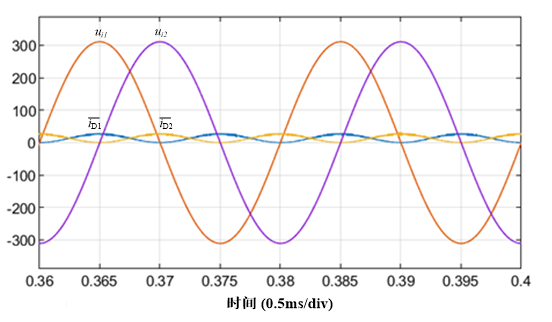
图14两组PFC的输入电压与二极管电流均值波形
4 结论
单相功率因数校正器(PFC)中升压电感过零交越失真,除了控制策略不当和功率器件(功率开关和无源器件)引起压降原因以外,主要是网压过零之后一段角度内,实际电感电流上升斜率明显低于期望电感电流上升斜率或在数值上不存在优势,基于实际电感电流与期望电感电流的斜率关系,给出了三种在升压电感输出端引入负电压的三种改进拓扑,可以有效解决和缓解升压电感过零交越失真。此外,简述了Scott变压器和LeBlanc变压器的接线关系和相量关系,给出了基于三相-两相平衡变压器以及单相功率因数校正器的三相AC-DC整流器在航空机载领域的工作原理和应用可能性。
参考文献
[1] 电磁兼容性(EMC). 第3-2部分: 限值. 谐波电流发射限值(设备输入电流为每相: IEC 61000—3-2-2005[S]. 2005.
[2] 电磁兼容性(EMC). 第3-12部分: 限值. 连接到带输入电流16 A至75 A每相公共低压系统的设备产生的谐波电流用限制. 释义表单1: IEC 61000—3-12 Interpretation Sheet 01-2012[S]. 2012.
[3] 国家标准化管理委员会. 电磁兼容 限值 第1部分:谐波电流发射限值(设备每相输入电流≤16 A): GB 17625.1—2022[S]. 2022.
[4] 全国电磁兼容标准化技术委员会. 电磁兼容限值每相输入电流大于16 A小于等于75 A连接到公用低压系统的设备产生的谐波电流限值: GB/T 17625.8-2015[S]. 2015.
[5] 全国电磁兼容标准化技术委员会. 电磁兼容 限值 对额定电流≤75 A且有条件接入的设备在公用低压供电系统中产生的电压变化、电压波动和闪烁的限制: GB/T 17625.7—2013[S]. 2013.







共0条 [查看全部] 网友评论