胡顺全，崔兆蕾，马得银，杨启航

（新风光电子科技股份有限公司，济南 250100）

A SOC estimation method of power battery based on improved EKF algorithm

HU ShunQuan，CUI Zhaolei, MA DeYin, YANG QiHang

 (WindSun Science & Technology Co., Ltd. Jinan 250100, Shandong Province, China)

Abstract: Aiming at the problem of inaccurate SOC(state-of-charge) estimation in the battery management system of energy storage systems, a SOC estimation method based on improved EKF algorithm was proposed. Matlab/Simulink simulation shows that this algorithm can realize rapid convergence of SOC initial values and effectively solve the problems of inaccurate SOC initial values and cumulative errors.

Key words：lithium-ion battery; battery model; EKF algorithm; SOC estimation; parameter modification;

摘要：针对储能系统中电池管理系统中SOC（电池荷电状态）估算不准确问题，提出一种基于改进EKF算法的SOC估算方法。通过Matlab/Simulink仿真验证表明该算法能够实现SOC初始值快速收敛，有效解决SOC初始值不准确和累积误差问题。

关键词：锂离子电池；电池模型；改进EKF算法；SOC估算；参数修正；

1  引言

电池管理系统（BMS）作为储能系统的关键部件，主要功能包括防止电池过充、过放、单体电压采集、模组温度信息采集、系统电流和端电压信息采集、电芯均衡、故障诊断与保护、SOX估算以及与EMS和充放电设备通讯等。其中SOC估算技术是BMS的核心技术的重要内容，也是国内外学者的研究重点之一。

目前，电池SOC估算技术主要有安时积分法、开路电压法、卡尔曼滤波算法和神经网络算法等^[8][11][12]。其中安时积分法简单易行，但是存在无法确定SOC初始值问题，初始值只能靠标定来确定，并且存在误差累积问题^[4]；基于开路电压法的SOC估算值误差会随着电池寿命的降低变得越来越大，并且不能够实现SOC实时监测；神经网络法需要依靠大量数据的训练，并且误差受训练数据的准确度和训练方法影响非常大，这要求BMS主控芯片要有非常高的性能，实际应用中很难满足，并且不具备成本优势；卡尔曼算法主要用于线性时变模型，而扩展卡尔曼算法能够弥补这一劣势，可以很好的应用于非线性系统，准确的反映电池系统内部动态参数。本文提出一种基于改进EKF（扩展卡尔曼算法）的SOC估算方法，解决安时积分法无法确定初始值和累计误差问题，同时能避免开路电压法不能够实现在SOC线监测和随电池寿命降低存在的SOC估算不准确问题，且与神经网络法相比更具成本优势，也不需要大量数据训练更易实现。

2  锂电池简化电化学模型

常见的电池模型主要有等效电路模型、自适应模型模型和电化学模型。其中等效电路模型不能很好的反映电池内部实时变化的特性。自适应模型依靠大量电池数据的训练，且对硬件要求较高，不适应当前实际应用；电化学模型参数较多，模型较为复杂且计算量较大。与等效电路模型不能够反映锂电池内部化学机理过程和电化学模型过于复杂的计算过程相比，简化电化学模型在保证估算精度的前提下有效降低了模型的复杂度和计算量，更加具备实际应用价值。本文选择简化电化学模型结合扩展卡尔曼算法进行SOC估算，其中锂电池简化电化学模型数学模型如下： 

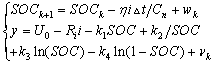      (1)

式中: 表示K时刻电池状态的值，表示电池初始时刻的值；是充放电效率,是一个检测值或经验值，一般取99.5%；是充放电电流，充电为负，放电为正； 表示锂电池的初始容量；Δt为采样时间；y是端电压；表示SOC估算模型的系统噪声，系统噪声指系统状态量变化引起的误差，是观测噪声，观测噪声指观测器引起的误差。是电池组的初始端电压或者开路电压，是电池组内阻，(i= 1～4)为实时估计的时变参数。

3  SOC估算与仿真分析

3.1  基于改进EKF的SOC估算

针对式（1）数学模型，选取SOC作为状态变量，作为输入量，作为输出量，可得到结合简化电化学模型的EKF的状态方程和观测方程，如式（2）所示。

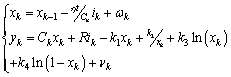    (2)

对式（2）进行一阶泰勒展开线性化，得到：

    (3)

其中为SOC的非线性函数。然后根据EKF估算过程进行估算：

（1）预测矩阵:

      (4)

预估的状态估计误差协方差：

           (5)

（2）更新的卡尔曼滤波增益:

      (6)

滤波方程：

 (7)

状态估计误差协方差：

          (8)

其中：是前一时刻的估计值，是当前时刻的最优估计值，为系统白噪声，均值为零；是k时刻系统的协方差矩阵；是均值为零的测量白噪声序列； 为k时刻观测噪声的协方差矩阵；是更新的卡尔曼滤波增益； 是更新的状态估计误差协方差。

锂电池模型是一个非线性系统，当系统噪声和观测噪声受电池非线性因素的影响较大时，上述EKF算法得到的SOC估算结果的精度就会下降，从而引起SOC估算值出现偏差，造成锂电池出现过充或过放问题。为防止SOC估算值出现偏差导致锂电池过充或过放问题的出现，本文采用查表法对锂电池不同温度和不同状态下的充放电电流进行滤波增益修正；并且在充电末端和放电末端采用SOC-OCV参数对SOC估计值进行修正，保障SOC在充放电末端不会出现过充与过放问题，从而得到SOC的最优估计值，完成对SOC的估算。SOC的估算过程如图1所示。

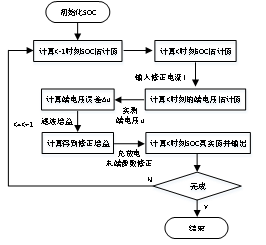
图1  SOC估算流程图

3.2  仿真分析与实验验证

该SOC估算方法，通过Matlab/Simulink进行仿真实验验证，实验通过设定不同，验证SOC估算值的变化曲线，并且在脉冲电流和恒流电流两种工况环境下进行仿真实验，分别验证SOC的估算结果的准确性和的收敛情况。

在脉冲电流工况环境下，SOC估算仿真过程如下，给定脉冲电流如图2所示。脉冲电流工况下，输出端电压仿真变化曲线如图3所示。

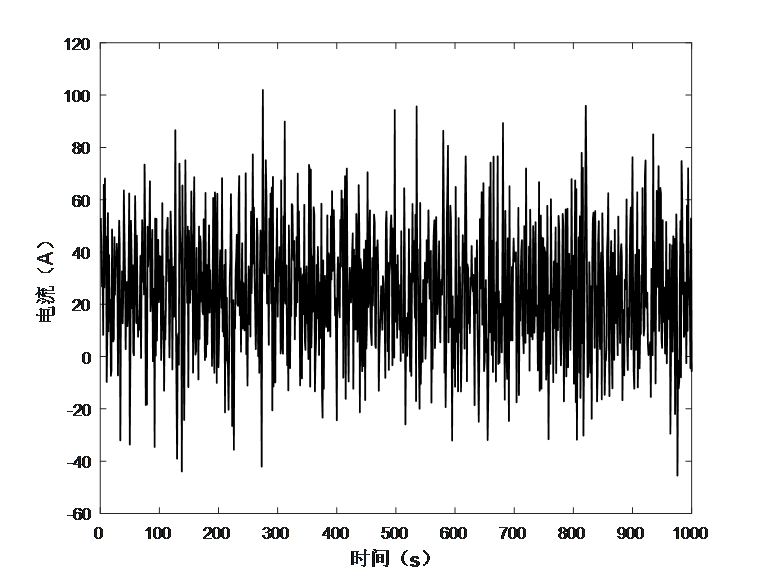
图2 脉冲电流波形图

   图3 脉冲工况下端电压波形图

脉冲电流工况下，针对不同SOC初始值下工作状态做了仿真测试验证，通过选取不同的SOC初始值，得到SOC初始值的收敛情况以及过程估算结果，详细的估算结果以及估算误差如以下所示。

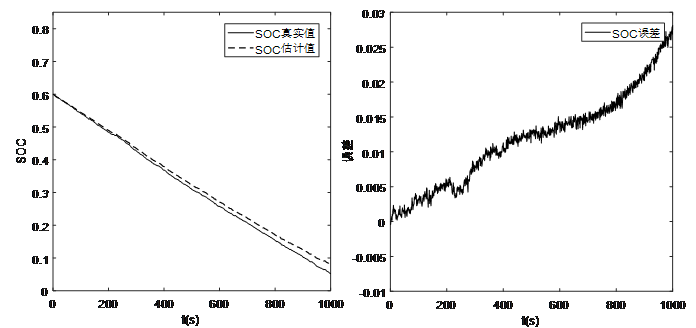
图4 脉冲放电SOC₀=60%估算曲线及误差

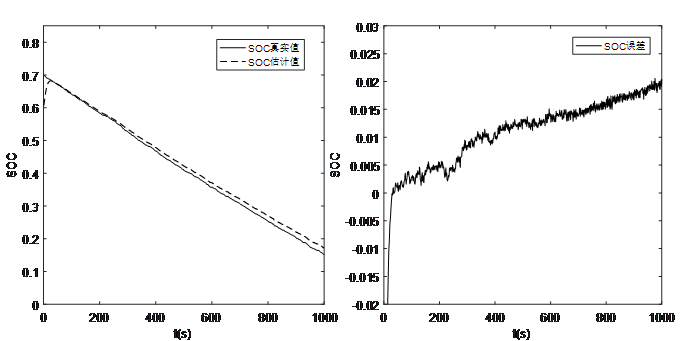
图5 脉冲放电SOC₀=70%估算曲线及误差

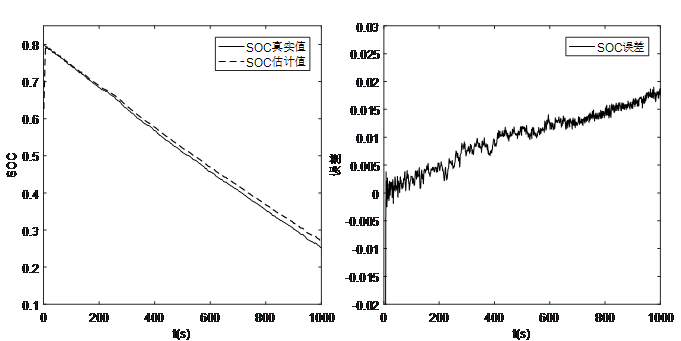
  图6 脉冲放电SOC₀=80%估算曲线及误差

由图4、图5和图6的仿真结果可以看出，在脉冲放电工况环境下，SOC初始值可以快速收敛到真实值附近，并且SOC估算误差保持在3%以内，表明在脉冲电流工况下，该方法能够实现SOC初始值的快速收敛，并具备较高的SOC估算精度。

恒流工况环境下，给定恒流电流波形如图7所示。对应输出端电压波形如图8所示。

图7  恒流电流波形图

    图8  恒流工况下端电压波形图

恒流工况下，针对不同SOC初始值进行了仿真测试验证，通过设置多组不同SOC初始值，获取到SOC估算结果和误差如下所示。

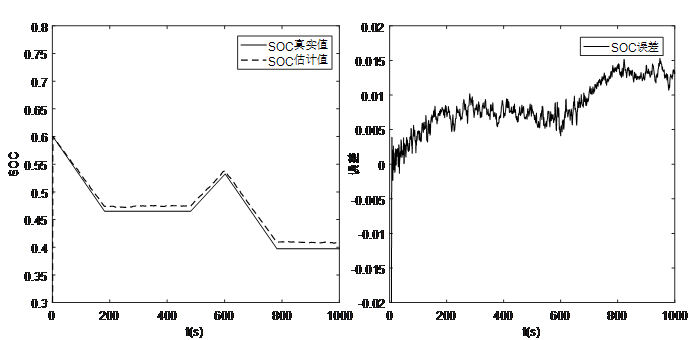
图9 恒流SOC₀=60%估算曲线及误差

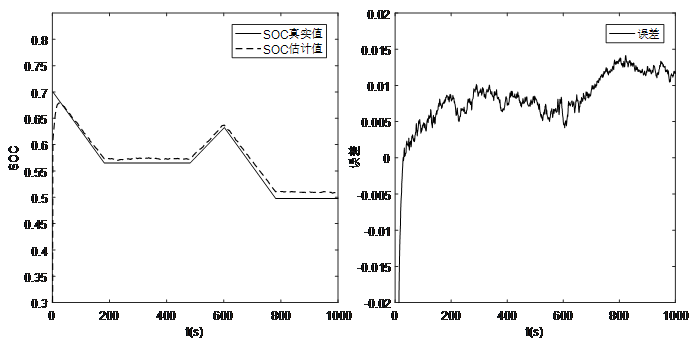
图10 恒流SOC₀=70%估算曲线及误差

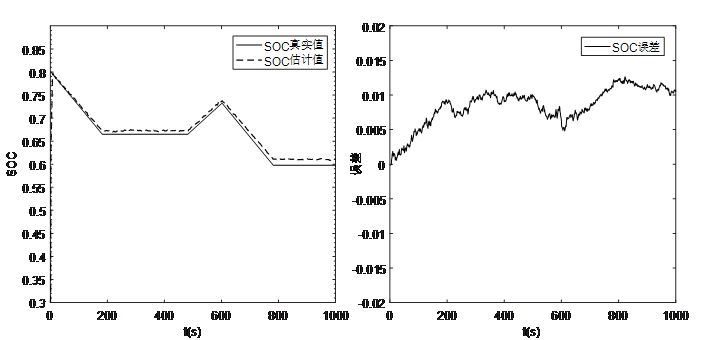
图11 恒流SOC₀=80%估算曲线及误差

恒流工况下，进行了放电、静置、充电等一系列实验流程模拟测试，得到了详细的运行状态数据。根据图9、图10和图11的仿真结果可以看出，不同SOC初始值下SOC估计值均能够快速收敛到真实值附近，且在充放电过程中，SOC估算误差一直保持在2%以内。证明该方法在恒流充放电工况下，能够实现SOC初始值的快速收敛，并且准确的进行SOC估算，具备良好的SOC估算精度。

4  结论

本文采用简化电化学电池模型结合EKF算法对电池SOC值进行估算，文章介绍了电池的简化电化学模型和EKF算法的递推原理。简化电化学模型反映锂电池的动态工作过程，结合扩展卡尔算法实现对SOC的实时推算，从而得到SOC的估算值。另外在估算过程中通过观察误差的大小，采用查表法对锂电池不同温度和不同状态下的充放电电流进行滤波增益修正，解决了EKF算法因系统噪声和预测噪声受电池非线性的影响而导致精度下降问题；在充电末端和放电末端采用SOC-OCV参数对SOC估计值进行修正，避免了SOC估算出现偏差造成的过充和过放问题。该方法在Matlab/Simulink仿真平台上完成了仿真实验验证，证明了该方法的可行性，且SOC初始值能够实现快速收敛，SOC估算误差在3%以内，较传统SOC估算方法相比，SOC估算精度有明显提高，具备实际应用价值。

参考文献

[1] ZHOU Y, LI X. Overview of lithium-ion battery SOC estimation［J］. IEEE International Conference on Information and Automa-tion，IEEE，2015: 2 454 － 2 459.

[2] 钟国彬，何耀，刘新天，等 . 基于高阶非线性模型的铅酸蓄电池SOC 估计［J］. 蓄电池，2015，54( 4) : 166 － 169.

[3] 基于AEKPF算法对锂离子电池SOC与SOH的联合估计[J]. 张新锋;姚蒙蒙;宋瑞;崔金龙.江苏大学学报(自然科学版),2022(01)

[4] 基于改进安时积分法的动力电池SOC估算[J]. 汪伟;黄河;龙宇舟;王全;崔兆蕾;张天.客车技术与研究,2021(03)

[5]  基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 颜湘武;邓浩然;郭琪;曲伟.电工技术学报,2019(18)

[6] CHARKHGARD，FARROKHI M． State-of-charge esti-mation for lithium-ion batteries using neural networks and EKF［J］.IEEE Transactions on Industrial Electronics，2010，57( 12) : 4178-4187．

[7] LEE S，KIM J，LEE J，et al．State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge［J］. Journal of Power Sources，2008，185( 2) : 1367-1373．

[8]  基于改进EKF算法的锂离子电池SOC估算方法[J]. 张方亮.电源学报,2018(05)

[9]  基于GRU-UKF的锂离子电池SOC估计方法研究[J]. 高峰;贾建芳;元淑芳;李孟威.电子测量与仪器学报,2022(11)

[10] 基于双无迹变换的锂离子电池SOC估计研究[J]. 封居强;孙亮东;蔡峰;伍龙;卢俊.电源技术,2022(11)

[11] 基于神经网络的老化锂电池SOC估算方法的研究[J]. 张立佳;徐国宁;赵向阳;杜晓伟;周翔.电源学报,2020(01)

[12] Yuhei Okazaki, Masanobu Yoshida, Kenichiro Fujiwara, Charging Method of EDLCs by Wind Power Generation in Stand Alone System[C], The 2010 International Power Electronics Conference, 2010, 2577-2584

—————————————————————————

作者简介：胡顺全(1976)，男，硕士研究生，正高级工程师，主要从事电力电子技术及储能方面的研究工作。

该文章得到“泰山产业创新领军人才工程资助”。