朱云龙(Zhu Yunlong) 1陈源宝(Chen Yuanbao)2*张向鹏(Zhang Xiangpeng)2吴雨芮(Wu Yurui)1
1 华中科技大学 2 武汉第二船舶设计研究所
关键词:非线性扰动观测器;自适应滑模控制;UUV轨迹跟踪;抖振抑制
Abstract: To address the challenges of model uncertainties, parameter perturbations, and unknown external disturbances encountered by unmanned underwater vehicles (UUVs) in complex marine environments, this paper proposes a composite motion control method integrating a disturbance observer with adaptive sliding mode control. Firstly, a six-degree-of-freedom (6-DOF) kinematic and dynamic model of the UUV is established, and a sliding surface is constructed to enhance convergence rate. Secondly, a finite-time disturbance observer is designed to estimate and compensate for lumped system disturbances in real time, effectively mitigating chattering phenomena in sliding mode control. Furthermore, an adaptive update law is introduced to dynamically adjust switching gain parameters, eliminating the dependency of traditional sliding mode control on prior knowledge of disturbance upper bounds. The finite-time convergence characteristics of the closed-loop system are rigorously proven using Lyapunov stability theory. Simulation results demonstrate that, compared with conventional sliding mode control, the proposed method significantly reduces trajectory tracking errors under unknown disturbance conditions.
Keywords: Nonlinear disturbance observer; Adaptive sliding mode control; UUV trajectory tracking; Chattering suppression
1. 引言
水下机器人(Unmanned Underwater Vehicle, UUV)作为深海探索与海洋工程的核心装备,在海底资源勘探[1]、环境监测[2]、应急救援[3]及水下设施运维等领域展现出独特价值。随着任务场景向深海、强干扰环境拓展,UUV控制系统的性能需求呈现多维度升级:轨迹跟踪精度需达厘米级,动态响应时间要求缩短至秒级,同时需在参数摄动、海流突变等复杂条件下保持强鲁棒性[4,5]。然而,其动力学模型存在显著非线性(如科氏力耦合效应)、水动力参数时变特性及随机干扰,传统控制方法面临精度与稳定性的双重挑战[6]。
针对上述问题,学界相继提出多种控制策略并取得阶段性进展:经典方法中,比例-积分-微分控制(PID)因结构简单被广泛采用[7],但其线性本质难以匹配UUV强耦合非线性特性,且在多输入多输出(MIMO)系统中参数整定效率低下[8];模糊逻辑控制(FLC)通过专家经验构建规则库降低模型依赖性[9],但规则更新滞后性导致其在突发干扰下适应性不足[10];滑模控制(SMC)凭借对匹配扰动的完全鲁棒性崭露头角[11],然而传统线性滑模面存在收敛速度慢、稳态误差大等固有问题,且切换增益过高会引发控制输入高频抖振[12]。先进方法中,神经网络控制通过非线性映射能力提升模型适应性[13],但需海量训练数据支撑且存在局部极小风险;深度强化学习(Deep Reinforced Learning,DRL)通过环境交互优化策略[14],但高维状态空间导致计算复杂度呈指数增长;模型预测控制(MPC)基于滚动优化处理约束问题[15,16],但实时求解非凸优化问题对嵌入式平台算力要求苛刻。值得注意的是,现有研究在参数自适应性方面仍存在显著局限:固定增益滑模控制需依赖扰动上界先验知识,而海洋干扰幅值常呈现非平稳特性[17],造成保守性控制或抖振加剧。为此,本文提出一种基于扰动观测器和自适应滑模的UUV轨迹跟踪控制策略,创新性体现于通过观测器精确估计系统集总扰动,减小控制输入的抖振,提高控制器的抗干扰性能。
全文架构如下:第2节建立UUV运动学和动力学模型;第3节详述NDOASMC控制器的设计与李雅普诺夫稳定性证明;第4节通过数值仿真验证方法有效性;第5节总结结论。
2. UUV运动学和动力学建模
对于UUV的运动特征,构建惯性坐标系与随体坐标系。以地球质心为原点的惯性坐标系![]() 和在UUV本体上的随体坐标系
和在UUV本体上的随体坐标系![]() ,具体如图1所示。
,具体如图1所示。
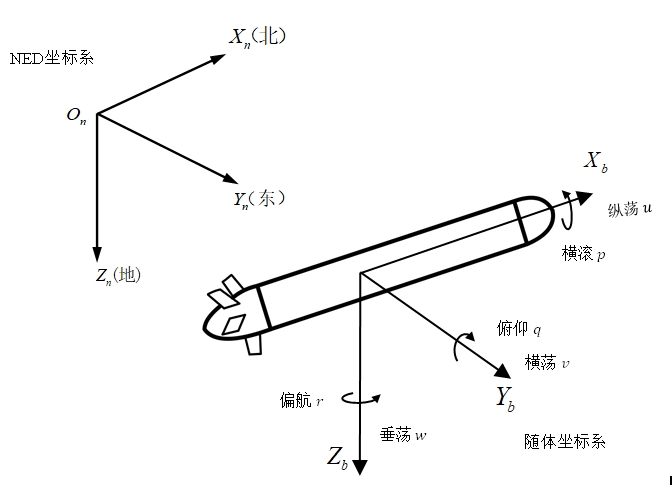
图1 UUV的惯性坐标系和随体坐标系
UUV的运动学方程如下:
![]() (1)
(1)
其中:![]() 为UUV在惯性坐标系下的位置及姿态,
为UUV在惯性坐标系下的位置及姿态,![]() 为分别指向UUV的轴向、横向与竖直向下方向唯一,
为分别指向UUV的轴向、横向与竖直向下方向唯一,![]() 分别为横摇角,俯仰角,偏航角,描述UUV在惯性坐标系下的姿态,向量
分别为横摇角,俯仰角,偏航角,描述UUV在惯性坐标系下的姿态,向量![]() 为随体坐标系下的速度,包括线速度
为随体坐标系下的速度,包括线速度![]() 和角速度
和角速度![]() 。
。![]() 为随体坐标系到惯性坐标系的转换矩阵,具体形式如下:
为随体坐标系到惯性坐标系的转换矩阵,具体形式如下:
![]() (2)
(2)
UUV的动力学方程是建立在UUV的受力和加速度上的关系方程。将UUV视作刚体,动力学方程为:
![]() (3)
(3)
其中![]() 为惯性矩阵,
为惯性矩阵,![]() 为UUV刚体的质量矩阵,
为UUV刚体的质量矩阵,![]() 是UUV的附加惯性矩阵,具体形式如下:
是UUV的附加惯性矩阵,具体形式如下:
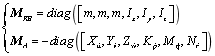 (4)
(4)
式中![]() 为向心力动力学矩阵,由科氏力
为向心力动力学矩阵,由科氏力![]() 和
和![]() 附加科氏力矩阵组成,具体表现形式如下:
附加科氏力矩阵组成,具体表现形式如下:
![]() (5)
(5)
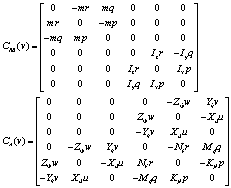 (6)
(6)
式(3)中
![]() (7)
(7)
其中![]()
![]()
![]() 都是可以测量的流体动力学系数。
都是可以测量的流体动力学系数。
式(3)中![]() 为恢复力向量,
为恢复力向量,![]() 为控制输入向量。具体表达式如下:
为控制输入向量。具体表达式如下:
![]() (8)
(8)
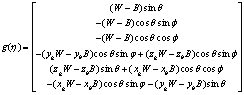 (9)
(9)
式(3)中![]() 为未知海洋扰动力和力矩矢量,包括水动力扰动、洋流等。
为未知海洋扰动力和力矩矢量,包括水动力扰动、洋流等。
3. 控制器设计与稳定性分析
3.1 自适应滑模轨迹跟踪控制器设计
针对UUV在未知扰动环境下的精确轨迹跟踪需求,本研究设计扰动观测器和自适应滑模的控制架构。利用Lyapunov函数构建稳定性判据,确保控制器在未知扰动情况下仍然保证全局收敛,鲁棒性大大增强。
滑模面设计是滑模控制理论的基石,其本质在于将复杂的系统跟踪问题转化为滑模流形上的稳定问题。在非线性系统中,由于模型不确定性、外部扰动及多自由度耦合的存在,通过滑模面设计引导系统误差动态趋于理想平衡点,是实现高精度控制的核心挑战。误差动力学通过数学描述跟踪误差的时域演化规律,揭示了系统未建模动态与外部干扰对控制性能的影响机制,为滑模面的参数化设计与稳定性分析提供了理论依据。对于n阶系统,滑模面通常设计为误差及其导数的线性组合。本文设计UUV的三维轨迹跟踪控制器。定义位置跟踪误差为
![]() (10)
(10)
对于二阶非线性系统,滑模面可设计为线性滑模面,具体形式如下:
其中![]() 为误差收敛矩阵。
为误差收敛矩阵。
针对UUV六自由度非线性动力学模型,滑模控制律的设计目标是迫使系统状态在有限时间内收敛至滑模面![]() ,并沿滑模面实现鲁棒跟踪。控制律由等效控制和切换控制两部分构成:
,并沿滑模面实现鲁棒跟踪。控制律由等效控制和切换控制两部分构成:
等效控制律![]() 的作用是抵消系统的标准动态误差,使其在无扰动情况下滑模面动态稳定,基于滑模面导数
的作用是抵消系统的标准动态误差,使其在无扰动情况下滑模面动态稳定,基于滑模面导数![]() 的条件,假设扰动
的条件,假设扰动![]() ,可得:
,可得:
![]() (12)
(12)
切换控制![]() 一般作用是抑制扰动和系统建模动态误差,确保系统在滑模面上鲁棒稳定,具体形式为
一般作用是抑制扰动和系统建模动态误差,确保系统在滑模面上鲁棒稳定,具体形式为
![]() (13)
(13)
其中![]() 为切换增益矩阵,满足
为切换增益矩阵,满足![]() 。
。
由于实际系统中扰动上界![]() 通常是未知的,只是简单的取固定增益会出现一些问题,如果
通常是未知的,只是简单的取固定增益会出现一些问题,如果![]() 取值过大,则会加剧控制输入的抖振现象,另外一方面,发生突发扰动的时候无法有效控制,甚至会导致系统不稳定。
取值过大,则会加剧控制输入的抖振现象,另外一方面,发生突发扰动的时候无法有效控制,甚至会导致系统不稳定。
总控制律由等效控制律和切换控制律复合构成,具体形式如下:
![]() (14)
(14)
考虑到实际系统中扰动上界![]() 通常是未知的,我们通过动态调整切换增益
通常是未知的,我们通过动态调整切换增益![]() ,使其收敛至扰动的最小上界。
,使其收敛至扰动的最小上界。
定义自适应增益![]() 为扰动上界
为扰动上界![]() 的估计值,设计自适应更新律,具体形式为:
的估计值,设计自适应更新律,具体形式为:
![]() (15)
(15)
其中![]() 为增益系数,控制增益更新的快慢。
为增益系数,控制增益更新的快慢。
考虑到符号函数![]() 会带来系统抖振问题,将其修改为双曲正切函数
会带来系统抖振问题,将其修改为双曲正切函数![]() ,结合式,切换控制律具体形式为:
,结合式,切换控制律具体形式为:
![]() (16)
(16)
其中![]() 函数为双曲正切函数,
函数为双曲正切函数,![]() 为平滑参数向量。
为平滑参数向量。
当滑模面误差![]() 增大时,
增大时,![]() 快速增加以增强鲁棒性,当扰动减小时,
快速增加以增强鲁棒性,当扰动减小时,![]() 自动减小,避免不必要的抖振。
自动减小,避免不必要的抖振。
稳定性证明:
选择李雅普诺夫函数:
![]() (17)
(17)
由式、式可得:
![]() (18)
(18)
则:
![]() (19)
(19)
假设扰动是有界的,![]() ,可得:
,可得:
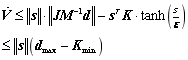 (20)
(20)
其中![]() ,选择
,选择![]() ,则有:
,则有:
![]() (21)
(21)
系统状态在有限时间内进入滑模面![]() ,随后沿滑模面指数收敛至原点。
,随后沿滑模面指数收敛至原点。
3.2扰动观测器设计
根据滑模控制器的设计原理,采用符号函数的切换项是其鲁棒性的主要来源。尽管选取足够大的正值K可确保其超越集总不确定性,但过大的K值会导致控制信号出现严重抖振。这种抖振可能损坏执行机构并造成显著的能量损耗。常见的减振方法是通过自适应律估计切换项系数,或引入扰动观测器对不确定性进行补偿。本研究接下来设计扰动观测器来抑制抖振现象。
考虑到未知扰动的环境,同时扰动会随时间不断变化,本文设计二阶扩张状态观测器(Second_order Extended State Observer, SESO)来估计扰动的大小。将扰动及其导数均视为扩展状态![]() ,系统方程扩展为:
,系统方程扩展为:
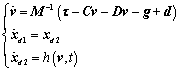 (22)
(22)
观测器方程具体形式如下:
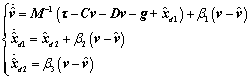 (23)
(23)
稳定性证明:
假设扰动变化率有界:![]() ,另外观测器增益
,另外观测器增益![]() 。选择Lyapunov函数:
。选择Lyapunov函数:
![]() (24)
(24)
其导数为:
![]() (25)
(25)
结合式(22)、式(23)可得:
![]() (26)
(26)
利用Cauchy-Schwarz不等式放缩:
![]() (27)
(27)
选择增益满足下面条件
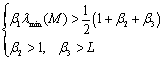 (28)
(28)
则有![]() ,误差系统全局渐进稳定。
,误差系统全局渐进稳定。
4. 仿真实验
基于上述理论分析,该控制方法在UUV轨迹跟踪控制中的有效性已得到验证。本节主要通过仿真验证控制器的稳定性与有效性。仿真所用控制器、非线性扰动观测器及自适应律参数如表1所示。系统集总不确定性数学模型如下:
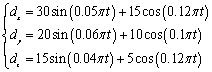 (29)
(29)
为进行定量比较分析,本文对所涉及的两种控制器的跟踪性能进行了定量评估。
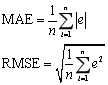 (30)
(30)
其中e表示误差量,用于表征控制过程中离散误差的大小。均方根误差![]() 对应于
对应于![]() 范数,而平均绝对误差
范数,而平均绝对误差![]() 对应于
对应于![]() 范数。
范数。
在Matlab仿真中,UUV初始状态设置为![]() ,
,
初始的姿态角及其导数设置为![]() 。
。
期望轨迹设计如下:
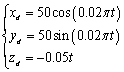 (31)
(31)
图2展示了未知扰动观测器的观测结果与设定值对比效果图。尽管观测器初始值与真实值存在较大偏差,但能快速收敛至准确估计值,表明所提出的观测器可为控制器设计提供可靠扰动估计。
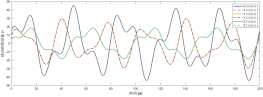
图2 扰动观测器估计位置扰动效果图
 (32)
(32)
根据MAE和RMSE的计算结果,提出的算法控制效果在抑制抖振和轨迹跟踪误差比传统方法更好。
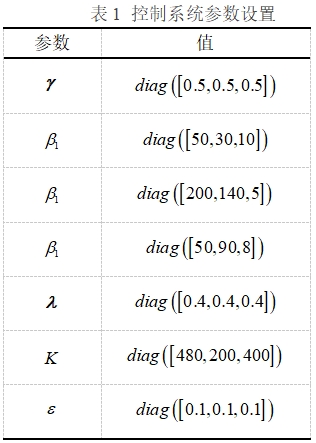
图3、图4展示了采用所提出的控制器后位置环的跟踪响应特性。可以明显观察到,在系统模型参数时变和存在外部干扰的情况下,本文提出的非线性扰动观测自适应滑模控制(NDOASMC)方法表现优异。图4展示了三个平移运动通道随时间的跟踪演化结果,表明当平移子系统受到显著扰动时,两种控制器均能实现良好的跟踪效果。图3则展示了三维螺旋上升运动轨迹。综合图3至图5可知,NDOASMC在位置环中较传统自适应滑模控制(ASMC)具有更快的跟踪速度和更高的控制精度。图5显示了位置跟踪误差的演化过程,NDOASMC能快速将误差控制在设定边界范围内,而ASMC虽可使误差收敛至近零附近,但存在明显波动。实验证明,所提出的控制器在控制精度和抑制抖振方面都优于传统ASMC方法。
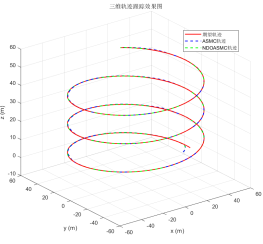
图3 三维空间UUV位置跟踪结果
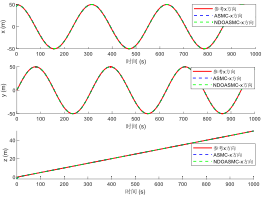
图4 UUV在x,y,z方向上跟踪效果
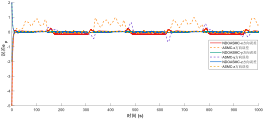
图5 UUV位置误差变化图
5. 结论
针对UUV的特点,本文提出了一种基于扰动观测器和自适应滑模控制的控制方法。针对UUV复杂的非线性动力学与外部扰动,通过扰动观测器来估计系统的集总不确定扰动,另外,通过自适应调节滑模控制器的增益参数,设计了高效的控制策略。
在仿真中,建立了包含质量矩阵、阻尼矩阵以及惯性项的完整水下机器人动力学与运动学模型,为控制器设计提供了理论基础。通过对两种算法的平均绝对误差(MAE)和均方根误差(RMSE)进行定量分析,与常规滑模控制方法对比,NDOASMC方法在抑制系统抖振以及控制器快速性都有较好的优越性。
尽管现阶段上述工作仍局限于理论建模分析与控制器设计,但其为水下自主航行器(UUV)的蓬勃发展及同类UUV控制器的设计提供了重要参考。在未来的工作中,将完成对于该算法的物理实验验证,展示该算法的价值。
6. 参考文献
[1] Chen Y, Liu Y, Meng Y, Yu S, Zhuang Y. System Modeling and Simulation of an Unmanned Aerial Underwater Vehicle. Journal of Marine Science and Engineering. 2019; 7(12):444。
[2] 唐军,吴涛,张少文.结合MPC与SMC的水下机器人轨迹跟踪控制算法[J/OL].机械科学与技术.1-9[2025-04-21].
[3] Lin R, Cao J, Xiao J, et al. Dynamic modeling and switching analysis of all-attitude multimode underwater vehicle for multidimensional data acquisition[J]. Ocean Engineering, 2023, 286: 115550.
[4] Tijjani A S, Chemori A, Creuze V. A survey on tracking control of unmanned underwater vehicles: Experiments-based approach[J]. Annual Reviews in Control, 2022, 54: 125-147.
[5] Hou Y, Liu J, Wang D, et al. Velocity and trajectory tracking control model for underactuated UUVs through coupling of direct CFD and PID control algorithm[J]. Ocean Engineering, 2024, 314: 119775.
[6] 杨昆,朱亚洲,王振宇,等.基于自适应反步滑模的AUV轨迹控制[J].舰船科学技术,2024,46(22):89-93.
[7] Hou Y, Liu J, Wang D, et al. Velocity and trajectory tracking control model for underactuated UUVs through coupling of direct CFD and PID control algorithm[J]. Ocean Engineering, 2024, 314: 119775.
[8] Tijjani A S, Chemori A, Roman G M. From non-model-based to adaptive model-based tracking control of low-inertia underwater vehicles[M]//Underwater vehicles: Design and applications. Nova Science Publishers, 2021: 35-66.
[9] Van M, Ge S S. Adaptive fuzzy integral sliding-mode control for robust fault-tolerant control of robot manipulators with disturbance observer[J]. IEEE Transactions on Fuzzy Systems, 2020, 29(5): 1284-1296.
[10] 李福仕,王通,郭静.基于变论域模糊PID的AUV靶标运动追踪控制[J].自动化应用,2024,65(13):41-45+48.
[11] 徐健,汪慢,乔磊,等.欠驱动UUV三维轨迹跟踪的反步动态滑模控制[J].华中科技大学学报(自然科学版),2015,43(08):107-113.
[12] Close J, Van M, McIlvanna S. PID-Fixed Time Sliding Mode Control for Trajectory Tracking of AUVs under Disturbance[J]. IFAC-PapersOnLine, 2024, 58(20): 281-286.
[13] 王景楠,薛晨阳,齐向东,等.基于RBF神经网络PID的UUV轨迹跟踪控制[J].中北大学学报(自然科学版),2024,45(06):843-851.
[14] He Z, Dong L, Sun C, et al. Asynchronous multithreading reinforcement-learning-based path planning and tracking for unmanned underwater vehicle[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 52(5): 2757-2769.
[15] 梅满,朱大奇,甘文洋,等.基于模型预测控制的水下机器人轨迹跟踪[J].控制工程,2019,26(10):1917-1924.
[16] Gan W, Zhu D, Hu Z, et al. Model predictive adaptive constraint tracking control for underwater vehicles[J]. IEEE Transactions on Industrial Electronics, 2019, 67(9): 7829-7840.
[17] 王庆楠,王娜,李广有,等.基于干扰观测器的AUV三维路径滑模跟踪控制[J].机械制造与自动化,2024,53(03):209-214.
作者简介:
朱云龙(2000-),男,华中科技大学人工智能与自动化学院,主要研究方向为UUV的轨迹跟踪和UUV集群的编队控制。
张向鹏(1997-),男,武汉第二船舶设计研究所,主要研究方向为电子信息技术。
吴雨芮(2001-),男,华中科技大学人工智能与自动化学院,主要研究方向为UUV集群的协同控制和基于视频的帕金森病运动迟缓定量评估。
通讯作者:
陈源宝(1983-),男,武汉第二船舶设计研究所,主要研究方向为电子信息技术。







共0条 [查看全部] 网友评论